Creating a Tri-Cylinder Intersection Surface with Pgfplots

Question

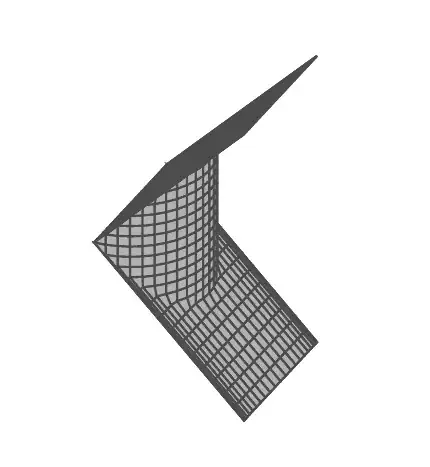
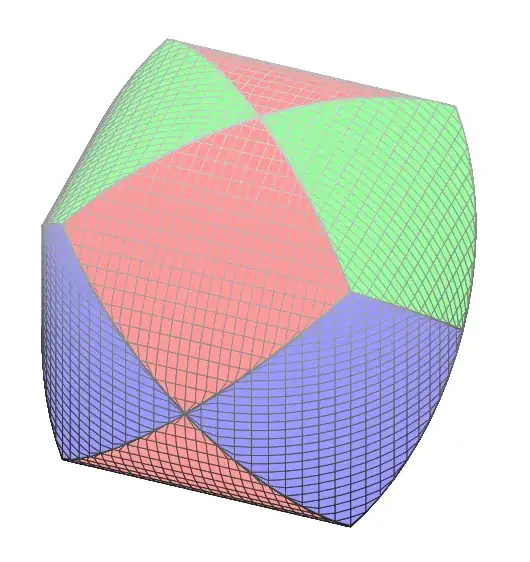
As an edit to provide further clarification (to save you some reading) - we are trying to define the second diagram parametrically, so that the two flat parts are truncated and we are just left with the part we can use for the diagram. Hope this Helps! Thanks

Have taken an interest in the techniques employed in this question: How to draw two intersecting cylinders?.

Specifically, since I'm still learning Asymptote, I want to the the pgfplots method to diagram the intersection surface of three cylinders. I got a diagram of three intersecting cylinders to work by fiddling around with the code, but am stuck on creating their surface of intersection.

Here's the diagram I have of the intersecting cylinders for reference (with credit to the inspiration, of course.) - see MWE #1 at the bottom:

And this is what I've got so far (if I can solve for one part, then I can do the rest) - see MWE #2:

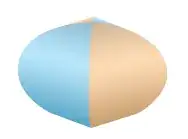
And what I want is something with this kind of shape, except corresponding to three cylinders instead of two - credit to Stewart:

MWE #1

\documentclass{article}
\usepackage{pgfplots}
\pgfplotsset{compat=1.18}
\begin{document}
\begin{center}
\begin{tikzpicture}[scale=3]
  \begin{axis}[%
        axis equal,
        enlargelimits = true,
        samples = 45, samples y = 45,
        axis lines = none, ticks = none,
        cyl/.style = {%
                surf,
                black!30!,
                variable = \u,
                variable y = \v,
                z buffer = sort,
                faceted color=black!70!,
                },
        %view/h = 125, view/v = 25
        ]
\addplot3[%         (-) Z-SEMIAXIS
    cyl,
    domain = -3:3,
    y domain = 0:360,
    ] ({cos(v)}, {sin(v)}, {min(u,abs(cos(v)),abs(sin(v)))});

\addplot3[%         (-) X-SEMIAXIS
    cyl,
    domain = -3:3,
    y domain = 0:360,
    ] ({min(u,-abs(cos(v)),-abs(sin(v)))}, {cos(v)}, {sin(v)});

\addplot3[%         (+) Y-SEMIAXIS
    cyl,
    domain = 0:360,
    y domain = -3:3,
    ] ({cos(u)}, {max(v,abs(cos(u)),abs(sin(u)))}, {sin(u)});

\addplot3[%         (+) X-SEMIAXIS
    cyl,
    domain = -3:3,
    y domain = 0:360,
    ] ({max(u,abs(cos(v)),abs(sin(v)))}, {cos(v)}, {sin(v)});

\addplot3[%         (+) X-SEMIAXIS
    cyl,
    domain = -3:3,
    y domain = 0:360,
    ] ({cos(v)}, {sin(v)}, {max(u,abs(cos(v)),abs(sin(v)))});

\addplot3[%         (-) Y-SEMIAXIS
    cyl,
    domain = 0:360,
    y domain = -3:3,
    ] ({cos(u)}, {min(-abs(cos(u)),-abs(sin(u)),v)}, {sin(u)});

\end{axis}

\end{tikzpicture}
\end{center}
\end{document}

MWE #2

\documentclass{article}
\usepackage{pgfplots}
\pgfplotsset{compat=1.18}
\begin{document}
\begin{center}
\begin{tikzpicture}[scale=2]
  \begin{axis}[%
        axis equal,
        enlargelimits = true,
        samples = 45, samples y = 45,
        axis lines = none, ticks = none,
        cyl/.style = {%
                surf,
                black!30!,
                variable = \u,
                variable y = \v,
                z buffer = sort,
                faceted color=black!70!,
                },
        %view/h = 125, view/v = 25
        ]
\addplot3[%         (-) Z-SEMIAXIS
    cyl,
    domain = -3:3,
    y domain = 0:360,
  restrict z to domain=-2:2,
    ] ({max(abs(u),cos(v))}, {sin(v)}, {u});

\end{axis}

\end{tikzpicture}
\end{center}
\end{document}

Edit by @hpekristiansen:

Here is a picture of the intersection of three cylinders

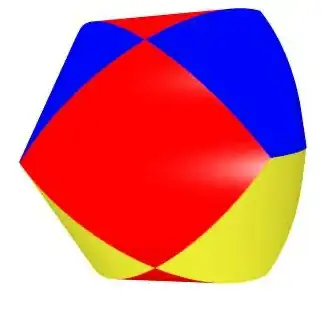
Found here: https://abel.math.harvard.edu/archive/21a_summer_06/handouts/3cylinder.pdf

hpekristiansen · Accepted Answer · 2024-01-26T10:06:05.800

\documentclass[tikz, border=1cm]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.18}
\begin{document}
\begin{tikzpicture}[line join=round]
\begin{axis}[
view={20}{40},
axis equal,
axis lines=none,
colormap/blackwhite,
cylinder/.style={
  surf, 
  domain=-1:1,
  samples=41,
  variable=\u, variable y=\v,
  z buffer=sort,
  ultra thin,
},
]

\addplot3[
cylinder, red!40,
y domain=0:270, %adjust domain to show front petals dependent on `view`
samples y=61,
x filter/.expression={
  (u>0)?
  ((cos(v)^2+u^2<1)&&(sin(v)^2+u^2<1)?u:(min( sqrt(1-cos(v)^2), sqrt(1-sin(v)^2)))):
  ((cos(v)^2+u^2<1)&&(sin(v)^2+u^2<1)?u:(max(-sqrt(1-cos(v)^2),-sqrt(1-sin(v)^2))))
},
] (u, {cos(v)}, {sin(v)});

\addplot3[
cylinder, green!40,
y domain=-90:90, %adjust domain to show front petals dependent on `view`
samples y=41,
y filter/.expression={
  (u>0)?
  ((cos(v)^2+u^2<1)&&(sin(v)^2+u^2<1)?u:(min( sqrt(1-cos(v)^2), sqrt(1-sin(v)^2)))):
  ((cos(v)^2+u^2<1)&&(sin(v)^2+u^2<1)?u:(max(-sqrt(1-cos(v)^2),-sqrt(1-sin(v)^2))))
},
] ({sin(v)}, u, {cos(v)});

\addplot3[
cylinder, blue!40,
y domain=180:360, %adjust domain to show front petals dependent on `view`
samples y=41,
z filter/.expression={
  (u>0)?
  ((cos(v)^2+u^2<1)&&(sin(v)^2+u^2<1)?u:(min( sqrt(1-cos(v)^2), sqrt(1-sin(v)^2)))):
  ((cos(v)^2+u^2<1)&&(sin(v)^2+u^2<1)?u:(max(-sqrt(1-cos(v)^2),-sqrt(1-sin(v)^2))))
},
] ({cos(v)}, {sin(v)}, u);

\end{axis}
\end{tikzpicture}
\end{document}

Daniel N · Answer 2 · 2024-01-26T14:39:08.043

One possibility is to construct each "half face" separately and to add them layer after layer depending on the view point. The parametrization of a face will have the form (cos(u), sin(u), max(cos(u), abs(sin(u)), v)) with -90<=u<=90 and 0<=v<=1.1 (for a cylinder parallel to the Oz axis).

The coordinates will be circularly permuted to obtain the other two cylinders.

Remark. The order is important and I only know how to do it by hand considering the observer's view point and by inspection of the output.

I insert below the intersection of two cylinders; the third coordinate is simpler in this case -- mxax(cos(u), v) -- since there are only two intersecting surfaces. But it shows that the case of three intersectiong cylinders is a natural generalization.

The code

\documentclass[11pt, margin=10pt]{standalone}
\usepackage{pgfplots}
\usepgfplotslibrary{colorbrewer}
\pgfplotsset{compat=1.17}
\usetikzlibrary[pgfplots.colormaps]
\begin{document}
\pgfplotsset{%
  cylinder piece/.style args={u domain=#1, cmap=#2}{%
    opacity = 1,
    surf,
    colormap/#2,
    shader=interp,
    z buffer = sort,
    samples = 33,  % 1 mod 4
    variable = \u,
    variable y = \v,
    domain = #1,
    y domain = 0:1.1,
  }
}
\iffalse  % 2 intersectiong cylinders
\begin{tikzpicture}
  \begin{axis}[axis equal,
    axis lines=none,
    view={130}{28}]
% z cylinder x&lt;0
\addplot3[cylinder piece={u domain={-90:90}, cmap=summer}]
({-cos(u)}, {sin(u)}, {-min(cos(u), v)});
\addplot3[cylinder piece={u domain={-90:90}, cmap=summer}]
({-cos(u)}, {sin(u)}, {min(cos(u), v)});

% x cylinder z&lt;0
\addplot3[cylinder piece={u domain={0:180}, cmap=autumn}]
({-min(sin(u), v)}, {cos(u)}, {-sin(u)});
\addplot3[cylinder piece={u domain={0:180}, cmap=autumn}]
({min(sin(u), v)}, {cos(u)}, {-sin(u)});

% x cylinder z&gt;0
\addplot3[cylinder piece={u domain={0:180}, cmap=autumn}]
({-min(sin(u), v)}, {cos(u)}, {sin(u)});
\addplot3[cylinder piece={u domain={0:180}, cmap=autumn}]
({min(sin(u), v)}, {cos(u)}, {sin(u)});

% z cylinder x&gt;0
\addplot3[cylinder piece={u domain={-90:90}, cmap=summer}]
({cos(u)}, {sin(u)}, {-min(cos(u), v)});
\addplot3[cylinder piece={u domain={-90:90}, cmap=summer}]
({cos(u)}, {sin(u)}, {min(cos(u), v)});

\end{axis}
\end{tikzpicture}
\fi
% \iffalse  % 3 intersecting cylinders
\begin{tikzpicture}
  \begin{axis}[axis equal,
    axis lines=none,
    view={130}{20}]
% y cylinder, x &lt; 0
\addplot3[cylinder piece={u domain={-90:90}, cmap=winter}]
({-cos(u)}, {-min(min(cos(u), abs(sin(u))), v)}, {sin(u)});
\addplot3[cylinder piece={u domain={-90:90}, cmap=winter}]
({-cos(u)}, {min(min(cos(u), abs(sin(u))), v)}, {sin(u)});

% z cylinder, x &lt; 0
\addplot3[cylinder piece={u domain={-90:90}, cmap=summer}]
({-cos(u)}, {sin(u)}, {-min(min(cos(u), abs(sin(u))), v)});
\addplot3[cylinder piece={u domain={-90:90}, cmap=summer}]
({-cos(u)}, {sin(u)}, {min(min(cos(u), abs(sin(u))), v)});

% x cylinder z &lt; 0
\addplot3[cylinder piece={u domain={0:180}, cmap=autumn}]
({-min(sin(u), abs(cos(u)), v)}, {cos(u)}, {-sin(u)});
\addplot3[cylinder piece={u domain={0:180}, cmap=autumn}]
({min(sin(u), abs(cos(u)), v)}, {cos(u)}, {-sin(u)});

% x cylinder z &gt; 0
\addplot3[cylinder piece={u domain={0:180}, cmap=autumn}]
({-min(sin(u), abs(cos(u)), v)}, {cos(u)}, {sin(u)});
\addplot3[cylinder piece={u domain={0:180}, cmap=autumn}]
({min(sin(u), abs(cos(u)), v)}, {cos(u)}, {sin(u)});

% z cylinder, x &gt; 0
\addplot3[cylinder piece={u domain={-90:0}, cmap=summer}]
({cos(u)}, {sin(u)}, {-min(min(cos(u), abs(sin(u))), v)});
\addplot3[cylinder piece={u domain={-90:0}, cmap=summer}]
({cos(u)}, {sin(u)}, {min(min(cos(u), abs(sin(u))), v)});

% y cylinder, x &gt; 0
\addplot3[cylinder piece={u domain={-90:90}, cmap=winter}]
({cos(u)}, {-min(min(cos(u), abs(sin(u))), v)}, {sin(u)});
\addplot3[cylinder piece={u domain={-90:90}, cmap=winter}]
({cos(u)}, {min(min(cos(u), abs(sin(u))), v)}, {sin(u)});

% half z cylinder, x &gt; 0
\addplot3[cylinder piece={u domain={0:90}, cmap=summer}]
({cos(u)}, {sin(u)}, {-min(min(cos(u), abs(sin(u))), v)});
\addplot3[cylinder piece={u domain={0:90}, cmap=summer}]
({cos(u)}, {sin(u)}, {min(min(cos(u), abs(sin(u))), v)});

\end{axis}
\end{tikzpicture}
% \fi
\end{document}

Thank you! The order is definitely important. May I ask why you are using pgfplots 1.9? — , Jan 26 '24 at 13:26
Yes, 1.9 but you can use 1.7 also, or an older version. There is nothing special in the code (like a tikz command). — Daniel N, Jan 26 '24 at 13:29
Why not use a newer version, such as 1.18? Is there something deficient about the newer versions? — , Jan 26 '24 at 13:33
No! There was a mistake. I copied the p;reamble for an old file and I payed no attention. I modified the code accordingly: compat=1.17. — Daniel N, Jan 26 '24 at 14:38

Creating a Tri-Cylinder Intersection Surface with Pgfplots

MWE #1

MWE #2

2 Answers2