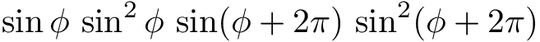Need help re-defining the basic trig functions

Question

I'd like to define my own commands to replace \sin, \cos, \tan, etc... I'd like to be able to use \tan[a]{x} to mean \tan^{a}{(x)}, and \tan{x} to mean just \tan{(x)}.

I've tried modeling a solution based on something I found online for having a command with an optional parameter, but I can't seem to get it to work.

\let\sin\oldsin

\def\sin{\@ifnextchar[{\@with}{\@without}}
\def\@with[#1]#2{\oldsin^{#1}{(#2)}}
\def\@without#1{\oldsin{(#1)}}

It complains about \oldsin not being a command.

I'd also like this to be able to function in combination with another command I made:

\renewcommand\arcsin[1]{\sin[-1]{(#1)}}

Answer 1

If you use amsmath (and I recommend you do), the definition of \sin is

\renewcommand\sin{\qopname\relax o{sin}}

so you just need something like

\renewcommand\sin[1][]{\qopname\relax o{sin}%
  \ifx\relax#1\relax\else^{#1}\fi % test if the argument is empty
}

Doing this for all the functions is really annoying, so you can abstract it by

\newcommand{\changefunction}[1]{%
  \expandafter\renewcommand\csname#1\endcsname[1][]%
    {\qopname\relax o{#1}\ifx\relax##1\relax\else^{##1}\fi}}

and then

\changefunction{sin}
\changefunction{cos}
\changefunction{tan}

Finally, you can do

\renewcommand{\arcsin}{\sin[-1]}

Complete example:

\documentclass{article}
\usepackage{amsmath}

\newcommand{\changefunction}[1]{%
  \expandafter\renewcommand\csname#1\endcsname[1][]%
    {\qopname\relax o{#1}\ifx\relax##1\relax\else^{##1}\fi}}
\changefunction{sin}
\changefunction{cos}
\changefunction{tan}

\renewcommand{\arcsin}{\sin[-1]}

\begin{document}
$\sin\alpha+\sin[2]\alpha\ne\arcsin(1/2)$
\end{document}

From a LaTeX point of view I don't think you gain anything with these definitions:

\sin^{2}

is as easy to type as \sin[2] and clearer.

From a mathematical point of view, I find that the notation you want to use for the arcsine is ambiguous and confusing. If the exponent "2" means "square the sine", the exponent "–1" will mean to a student "the reciprocal of the sine".

Answer 2

The sequence \let\csA\csB copies \csB’s definition to \csA, so you need to use

\let\oldsin\sin

Furthermore, the original \sin does not take an argument. I’d drop the latter argument in both, so you can still write \sin\phi to be displayed as “sin φ” and not “sin(φ )”.

If you use LaTeX you can simply do

\renewcommand*{\sin}[1][]{\oldsin\if\relax\detokenize{#1}\relax\else^{#1}\fi}

and get the same without the need to create your own auxiliary macros.

Though, of you really want the second argument, use

\renewcommand*{\sin}[2][]{\oldsin\if\relax\detokenize{#1}\relax\else^{#1}\fi (#2)}

but then you have no control over the size of the parentheses (say with a \frac in display mode). In this case you also need to drop the parenthesis in the definition of \arcsin (to avoid having double parentheses).

Code

\documentclass{article}
\let\oldsin\sin

\renewcommand*{\sin}[1][]{\oldsin\if\relax\detokenize{#1}\relax\else^{#1}\fi}

\begin{document}
$ \sin \phi $

$ \sin[2] \phi $

$ \sin (\phi + 2\pi) $

$ \sin[2] (\phi +2\pi) $
\end{document}

Output

Answer 3

I agree with egreg that this interface doesn't actually save you any work and actually loses some clarity in the source. Here's how I have been handling these powers of trig function.

I use the cool package. It provides commands like \Sin and \Cos which automatically add parentheses of the right size. It also provides their inverses \ArcSin, etc., which can be configured for either the "arc" style or the "inverse" style. Since LaTeX only provides \arc-macros for sine, cosine, and tangent, though, you have to provide the others.

For powers, I wanted to be able to type \Sin{x}^2 and see it as if I had typed \sin^2(x). So I redefined \Sin to look for ^ and adapt.

\documentclass{article}
\newcommand{\arccot}{\operatorname{arccot}}
\newcommand{\arcsec}{\operatorname{arcsec}}
\newcommand{\arccsc}{\operatorname{arccsc}}
\usepackage{cool}
\makeatletter
\newcommand{\COOL@switch@arctrig}[2]{%
    \ifthenelse{\equal{\COOL@notation@ArcTrig}{inverse}}{#1}{%
        \ifthenelse{\equal\COOL@notation@ArcTrig{arc}}{#2}{%
            \PackageError{cool}{Invalid ArcTrig option: can be only `arc' or `inv'}%
        }%
    }
}
\renewcommand{\ArcCot}[1]{%
    \COOL@switch@arctrig{\cot^{-1}}{\arccot}%
    \COOL@decide@paren{ArcTan}{#1}%
}
\renewcommand{\ArcSec}[1]{%
    \COOL@switch@arctrig{\sec^{-1}}{\arcsec}%
    \COOL@decide@paren{ArcSec}{#1}%
}
\renewcommand{\ArcCsc}[1]{%
    \COOL@switch@arctrig{\csc^{-1}}{\arccsc}%
    \COOL@decide@paren{ArcCsc}{#1}%
}

\let\COOL@Sin@Nopower\Sin
\let\COOL@Cos@Nopower\Cos
\let\COOL@Tan@Nopower\Tan
\let\COOL@Cot@Nopower\Cot
\let\COOL@Sec@Nopower\Sec
\let\COOL@Csc@Nopower\Csc

\def\Sin#1{\@ifnextchar^{\COOL@Sin@Power{#1}}{\COOL@Sin@Nopower{#1}}}
\def\Cos#1{\@ifnextchar^{\COOL@Cos@Power{#1}}{\COOL@Cos@Nopower{#1}}}
\def\Tan#1{\@ifnextchar^{\COOL@Tan@Power{#1}}{\COOL@Tan@Nopower{#1}}}
\def\Cot#1{\@ifnextchar^{\COOL@Cot@Power{#1}}{\COOL@Cot@Nopower{#1}}}
\def\Sec#1{\@ifnextchar^{\COOL@Sec@Power{#1}}{\COOL@Sec@Nopower{#1}}}
\def\Csc#1{\@ifnextchar^{\COOL@Csc@Power{#1}}{\COOL@Csc@Nopower{#1}}}

\def\COOL@Sin@Power#1^#2{\sin^{#2}\COOL@decide@paren{Sin}{#1}}
\def\COOL@Cos@Power#1^#2{\cos^{#2}\COOL@decide@paren{Cos}{#1}}
\def\COOL@Tan@Power#1^#2{\tan^{#2}\COOL@decide@paren{Tan}{#1}}
\def\COOL@Cot@Power#1^#2{\cot^{#2}\COOL@decide@paren{Cot}{#1}}
\def\COOL@Sec@Power#1^#2{\sec^{#2}\COOL@decide@paren{Sec}{#1}}
\def\COOL@Csc@Power#1^#2{\csc^{#2}\COOL@decide@paren{Csc}{#1}}

\makeatother
\begin{document}
\begin{minipage}{0.4\textwidth}
\[
       \Style{ArcTrig=arc}
       \begin{aligned}
         \ArcSin{1} &= \frac{\pi}{2}  \\
         \ArcCos{1} &= 0              \\
         \ArcTan{1} &= \frac{\pi}{4}  \\
         \ArcCot{1} &= \frac{\pi}{4}  \\
         \ArcSec{1} &= 0              \\
         \ArcCsc{1} &= \frac{\pi}{2}  \\
       \end{aligned}
\]
\end{minipage}
\begin{minipage}{0.4\textwidth}
\[
       \Style{ArcTrig=inverse}
       \begin{aligned}
         \ArcSin{1} &= \frac{\pi}{2}  \\
         \ArcCos{1} &= 0              \\
         \ArcTan{1} &= \frac{\pi}{4}  \\
         \ArcCot{1} &= \frac{\pi}{4}  \\
         \ArcSec{1} &= 0              \\
         \ArcCsc{1} &= \frac{\pi}{2}  \\
       \end{aligned}
\]
\end{minipage}
\[
\Sin{x}^2 = \frac{1}{2}\left(1 - \Cos{2x}\right)
\]
\end{document}

I guess a disadvantage is that if you type \Sin x^2 you will get \sin^2(x) when you probably mean \sin(x^2). But the cool way is to embrace the arguments.