How can I force \left, \right delimiters to automatically (!) have the same size despite line breaks?

Question

This code

\documentclass{article}

\usepackage{amsmath}

\begin{document}
\begin{align*}
\begin{split}
    z = \left( a + b + c \right. \\ 
        \left. + \frac{d}{e} \right)
\end{split} 
\end{align*}
\end{document}

produces the following output:

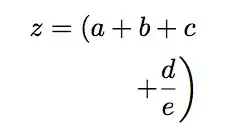
enter image description here

The two delimiters have different sizes. A common trick to obtain matching sizes is to use \vphantom like so:

\documentclass{article}

\usepackage{amsmath}

\begin{document}
\begin{align*}
\begin{split}
    z = \left( a + b + c +\vphantom{\frac{d}{e}}\right. \\  
        \left. + \frac{d}{e} \right)
\end{split} 
\end{align*}
\end{document}

which produces the following output:

enter image description here

However, such an approach

becomes rapidly complex as the number of line breaks increases;
is not maintainable at all (because, if a line's contents change, the argument of \vphantom may have to be modified as well to obtain the desired output).

Alternative approach 1: manually size the delimiters (using \big and the likes). Sadly, that's not very maintainable either.

Alternative approach 2: using some math environment provided by the breqn package, which allows for line breaks between two \left/\right delimiters and takes care of delimiter sizing. However, I'd like to stay away from breqn, if possible.

Can you think of a way to make associated \left/right\ delimiters to automatically have the same size despite line breaks, without (explicitly) using the \vphantom trick? Ideally, the solution should work for multiple nested pairs of delimiters. For example, in the following, the inner delimiters should have the same size and the outer delimiters should have the same size:

\left( \left( ... \right. \right. \\
\left. \left. ... \right) \right)

Why not use the fixed size delimiters, with \Big or even \biggl and \biggr and Co, as suggested by egreg in his answer to this question — Jhor, Jul 15 '13 at 17:20
You almost always get better spacing, even without line breaking if you use \bigr( ... \bigl) — David Carlisle, Jul 15 '13 at 17:22
@DavidCarlisle Yes, I could do that, but that's not very maintainable: I'd have to manually adapt the size of each delimiter depending on the contents of each line, which may change over the course of my writing the document. I'm wondering whether a better approach exists... — jub0bs, Jul 15 '13 at 17:32
It is more maintainable than using \left \right mainly because it works rather than not works. — David Carlisle, Jul 15 '13 at 17:35
@DavidCarlisle I see. Would you discourage using \left, \right in all cases? — jub0bs, Jul 15 '13 at 17:37
@Jubobs \left and \right do have their uses; in my documents you can surely find them. The fact is that most of the times I see them in others' input, they are misused. — egreg, Jul 15 '13 at 17:49
@egreg Thanks. Can you think of a canonical source (on TeX.SE or elsewhere) about cases in which using \left, \right is appropriate? I can't seem to find such a canonical answer on TeX.SE. If there is none, I will ask that question. — jub0bs, Jul 15 '13 at 17:54
@Jubobs Arrays and fractions are good candidates. When big operators with limits are involved, they're better not being used. — egreg, Jul 15 '13 at 17:56

score 18 · Accepted Answer · edited Jun 12 '17 at 17:24

The following example uses package zref to remember the size of the math formula in labels. Package mleftright is used to reduce the additional horizontal spacing by \left and \right.

Inside a complex math block, the following macros can be used:

\mzleft{<label>}{<left delimiter>}{<math formula>}
\mzright{<label>}{<math formula>}{<right delimiter>}

The macros can be nested, The <label> is needed to identify the pairs of delimiters. Inside the math block (math environment, ...) the <label> names for the pairs must be unique. After the math block \mzreset can be called. It frees the <label> names and they can be reused.

Example file:

\documentclass{article}

\usepackage{amsmath}
\usepackage{mleftright}
\usepackage{zref-base}

\makeatletter
\zref@newprop{mzheight}[0pt]{\the\ht\z@}
\zref@newprop{mzdepth}[0pt]{\the\dp\z@}
\newcount\c@@mz
\newcommand*{\the@mz}{mz\the\c@@mz}
\newcommand*{\@mz@list}{}    
\let\@mz@do\relax
\newcommand*{\mzreset}{%
  \begingroup
    \def\@mz@do##1{%
      \global\expandafter\let\csname mz@##1\endcsname\relax
    }%
    \@mz@list
    \global\let\@mz@list\@empty
  \endgroup
}
\newcommand*{\mzleft}[3]{%
  \@ifundefined{mz@#1}{%
    \global\advance\c@@mz\@ne
    \expandafter\xdef\csname mz@#1\endcsname{\the@mz}%
    \xdef\@mz@list{\@mz@list\@mz@do{#1}}%
  }{}%
  \expandafter\let\expandafter\@mz\csname mz@#1\endcsname
  \mleft#2%
  \expandafter\mathpalette\expandafter{%
    \expandafter\@mzleft\expandafter{\@mz}%
  }{#3}%
  \mright.\kern-\nulldelimiterspace
}
\newcommand*{\mzright}[3]{%
  \kern-\nulldelimiterspace
  \@ifundefined{mz@#1}{%   
    \@latex@warning{Missing \string\mzleft{#1}}%
    \mleft.#2\mright#3%
  }{%
    \expandafter\let\expandafter\@mz\csname mz@#1\endcsname
    \mleft.%
    \expandafter\mathpalette\expandafter{%
      \expandafter\@mzright\expandafter{\@mz}%
    }{#2}%
    \mright#3%
  }%
}   
\newcommand*{\@mzleft}{%
  \@mzleftright lr%
}
\newcommand*{\@mzright}{%
  \@mzleftright rl%
}
\newcommand*{\@mzleftright}[5]{%
  \sbox0{$\m@th#4{}#5{}$}%
  \ifmeasuring@
  \else
    \begingroup
      \let\@auxout\@mainaux
      \zref@labelbyprops{#3#1}{mzheight,mzdepth}%
    \endgroup
  \fi
  \zifrefundefined{\@mz #2}{%
  }{%
    \dimen@=\zref@extract{#3#2}{mzheight}\relax
    \ifdim\dimen@>\ht0 %
      \ht0=\dimen@
    \fi
    \dimen@=\zref@extract{#3#2}{mzdepth}\relax
    \ifdim\dimen@>\dp0 %
      \dp0=\dimen@
    \fi
  }%   
  \copy0\relax
}
\makeatother

\begin{document}
\begin{align*}
\begin{split}
    z = \mzleft{a}({ a + b + c +} \\
        \mzright{a}{{}+ \frac{d}{e}})
\end{split} 
\end{align*}   

\mzreset

\begin{align*}
\begin{split}
    z = \mzleft{a}{[}{%
          a + b + \frac{c}{d} +
          \mzleft{b}{(}{
            \int_0^\infty \mathrm{d}x
          }   
        } \\  
        \mzright{b}{
          + y}{)
        }
        \mzright{a}{
          + \frac{\displaystyle\sum_{i=0}^{100}i}{e}
        }{]}
\end{split}   
\end{align*}  
\end{document}

Thanks a lot, Heiko. A follow-up: could your solution be extended to handle more than two lines? — jub0bs, Jul 17 '13 at 18:14
@Jubobs: You have a left and a right delimiter, that means two lines, but arbitrary lines in between. Or do you mean to support e-TeX's \middle? — Heiko Oberdiek, Jul 17 '13 at 18:39
I'm afraid I'm not familiar with \middle, but what I meant is that a long equation may spread over more than two lines. — jub0bs, Jul 17 '13 at 19:39
@Jubobs: No problem, you can even put \mzleft and \mzright on different pages. The <label> of the first argument connects them. Only \mzreset must not occur in between, because it clears the <label> names. — Heiko Oberdiek, Jul 17 '13 at 21:25

score 8 · Answer 2 · edited Jul 15 '17 at 05:11

While I think that a) \bigls are preferable, and b) biglifying your delimiters is right up there with manual hyphenation and occasional \enlargethispages at the very end of proofreading, you may find that something like this makes them slightly more maintainable:

\newcommand\SPLIT[2]{%
  \left( #1\vphantom{#2}\right. \\
  \left. \vphantom{#1}#2\right) \\
}

\begin{align*}
  \begin{split}
    z= \SPLIT{a + b + c +}{d +\frac{d}{e}}
  \end{split}
\end{align*}

At least, it saves the manual repetiton of the sizing argument. I'm sure if one were sufficiently inclined, it could be extended to handle a variable number of lines, too.

user202729 · Answer 3 · 2022-12-05T10:18:12.803

Might worth mentioning: the nath package supports this, although it unfortunately is incompatible with a lot of other packages.

Taken straight from the documentation, with some modifications (*):

%! TEX program = lualatex
\documentclass{article}
\usepackage{nath}
\begin{document}
\[
\sin 2nx = 2n \cos x [\sin x \\
\qquad + \sum_{k = 1}^n (-4)^k
\frac{(n^2 - 1^2)(n^2 - 2^2) \dots (n^2 - k^2)}{(2k - 1)!}
\sin^{2k - 1} x]
\]
\end{document}

The output:

How can I force \left, \right delimiters to automatically (!) have the same size despite line breaks?

4 Answers4

Linked