18

I'm trying to replicate the following plot with PGFPlots:

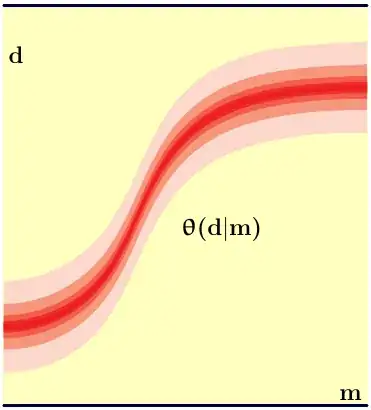
enter image description here

In this answer, the author plays with opacity when drawing overlapping ellipses. Is it possible to use similar code with arbitrary curves?

Ideally, the confidence intervals should be specified for every abscissa.

Do you have any hint on the software used to generate the plot above? Or any other suggestion (Matplotlib, R, ...)?

g.kov
  • 21,864
  • 1
  • 58
  • 95
juliohm
  • 3,452
  • Do you want to plot data, or a function? – Jake Oct 21 '13 at 13:08
  • Maybe some adaption of http://tex.stackexchange.com/a/80207/18674 might be possible, although it won't be easy especially for variable blurring widths. – Benedikt Bauer Oct 21 '13 at 13:18
  • @Jake, a well-formed expression y = f(x) where for each x in the domain of f we associate a deviation s. – juliohm Oct 21 '13 at 13:27
  • No sure if this helps or if it works, but theoretically this should be achieved with area plots, which are a combination of stack plots and \closedcycle (look for section "area plots" in the manual). For every color used, you'd have to provide the point coordinates of both the upper and lower curves, as a single closed path. To automatically blur a single curve sounds more difficult. – iavr Oct 21 '13 at 13:36
  • Thanks @iavr, but it seems area plots necessarily have to touch the x axis, and as you said, for a single curve the problem is different. – juliohm Oct 21 '13 at 13:45
  • Since the shape shown thins as the slope increases, I suspect he just filled in between two curves f(x)+w and f(x)-w. – John Kormylo Oct 21 '13 at 16:46
  • @JohnKormylo, shifting a graph f(x) +/- w with w a constant doesn't change its shape. This would mean at every abscissa the confidence interval is the same, which is not the case for the plot shown. – juliohm Oct 21 '13 at 16:53
  • The entire basis for calligraphy is that the thickness of a line depends on the angle of the stylus relative to its motion. – John Kormylo Oct 21 '13 at 23:14

4 Answers4

18

This is basically the same as Is there an easy way of using line thickness as error indicator in a plot?, only with functions instead of tabulated data. The trick is to use stack plots=y together with \closedcycle to create the bands.

I've defined a new command, \addplotwitherrorbands[<optional styles>]{<function>}{<positive error>}{<negative error>} that can be used as follows:

\documentclass[border=5mm]{standalone}
\usepackage{pgfplots}

\begin{document}

\tikzset{
    error band/.style={fill=orange},
    error band style/.style={
        error band/.append style=#1
    }
}

\newcommand{\addplotwitherrorband}[4][]{
    \addplot [#1, draw=none, stack plots=y, forget plot] {#2-(#3)};
    \addplot +[#1, draw=none, stack plots=y, error band] {(#3)+(#4)} \closedcycle;
    \addplot [#1, draw=none, stack plots=y, forget plot] {-(#2)-(#3)};

    \addplot [#1, forget plot] {#2};
}

\begin{tikzpicture}[
    declare function={f(\x)=rad(\x)-sin(\x);}
]
\begin{axis}[domain=0:360, enlarge x limits=false,
cycle list={
error band style=orange!20\\
error band style=orange!40\\
error band style=orange!60\\
error band style=orange!80\\
error band style=orange!100\\
}]

\pgfplotsinvokeforeach{1,0.5,0.25,0.125, 0.0625} {
    \addplotwitherrorband [] {f(x)}{#1}{#1}
}
\end{axis}
\end{tikzpicture}
\end{document}
David Carlisle
  • 757,742
Jake
  • 232,450
  • Very nice Jake! I'll investigate your solution carefully. – juliohm Oct 21 '13 at 22:03
  • why the following code does not compile? \foreach \dh/\clr in {1/20,0.5/40,0.25/60,0.125/80,0.0625/100} { \addplotwitherrorband[error band style=orange!\clr] {f(x)}{\dh*s(x)}{\dh*s(x)} }. It has something to do with the expansion for \clr. – juliohm Oct 24 '13 at 21:46
  • thanks for updating the answer. There is no way of setting the color within the loop? Having to explicitly type the cycle list is not "ideal". – juliohm Oct 24 '13 at 23:11
13

enter image description here

Check out if this MWE with Asymptote does what you need. For demonstration in this example it uses three paths (guides) gtop,gbot and gmid to define functions f(x) for mean and s(x) for deviation, use the proper definitions of f(x) and s(x) instead. Array pen[] clrs defines colors, array real[] dh defines fractions of the total interval to cover with the corresponding color. Then for every color the top (gt), bottom (gb) guides are defined and joined in a region g fo fill with i-th color.

% blurred.tex: 
%
\documentclass{article}
\usepackage{textgreek}
\usepackage[inline]{asymptote}
\usepackage{lmodern}
\begin{document}
\begin{figure}
\begin{asy}
size(200);
import graph;

pair[] botP={(0,0.09),(0.252,0.196),(0.383,0.429),(0.479,0.588),
(0.574,0.668),(0.733,0.726),(0.883,0.747),(1,0.747),};

pair[] topP={(0,0.341),(0.252,0.451),(0.383,0.677),(0.479,0.841),
(0.574,0.92),(0.733,0.977),(0.883,0.993),(1,1),};

pair[] midP=0.5*(topP+botP);

guide gtop=graph(topP,operator..);
guide gbot=graph(botP,operator..);
guide gmid=graph(midP,operator..);

real f(real x){
  real t=times(gmid,x)[0];
  return point(gmid,t).y;
};

real s(real x){
  real tt=times(gtop,x)[0];
  real tb=times(gbot,x)[0];
  return point(gtop,tt).y-point(gbot,tb).y;
};

real xmin=0, xmax=1;

pen[] clrs={
  rgb(0.988,0.847,0.796),
  rgb(0.969,0.592,0.502),
  rgb(0.953,0.365,0.29),
  rgb(0.933,0.188,0.165),
  rgb(0.933,0.114,0.137),
};

real[] dh={1,0.5,0.25,0.125,0.0625};

guide gt, gb,g;

for(int i=0;i<clrs.length;++i){
  gt=graph(new real(real x){return f(x)+0.5dh[i]*s(x);},xmin,xmax);
  gb=graph(new real(real x){return f(x)-0.5dh[i]*s(x);},xmin,xmax);
  g=gb--reverse(gt)--cycle;
  fill(g,clrs[i]);
}

real ymax=1.1;
pen axisPen=darkblue+1.3bp;
xaxis(xmin,xmax,axisPen);
xaxis(YEquals(ymax),xmin,xmax,axisPen);

label("\textbf{\straighttheta(d$|$m)}",(0.6,0.5));
label("\textbf{m}",(xmax,0),NW);
label("\textbf{d}",(0,1),SE);

shipout(bbox(Fill(paleyellow)));
\end{asy}
\end{figure}
\end{document}
%
% Process:
%
% pdflatex blurred.tex
% asy blurred-*.asy
% pdflatex blurred.tex
g.kov
  • 21,864
  • 1
  • 58
  • 95
  • Really?! This is awesome! I won't mark it as the final answer for the moment, just to see if one can reach similar quality with TikZ. Thank you very much. – juliohm Oct 21 '13 at 20:46
  • could you please elaborate on how to set the function y=f(x) within this code? I see you added points by hand. – juliohm Oct 21 '13 at 20:53
  • @juliohm: If you know the functions f(x) and s(x) (do you?), you don't need these manual points, just replace the body of their definitions inside real f(real x){...} and real s(real x){...} with the proper math expressions. – g.kov Oct 21 '13 at 21:25
  • I'll experiment setting the functions to grasp how it works. – juliohm Oct 21 '13 at 22:01
  • This is really nice solution, I'll mark it as the final answer. For new comers, ignore all Asymptote code before the definitions for f and s and simply write the analytical expressions, for example: return x - sin(x) and return 0.8. @g.kov, there is a confusion with the deviation interval, it should be f(x)+dh instead of f(x)+0.5dh. – juliohm Oct 22 '13 at 12:06
4

Inspired by g.kov answer, this is the TikZ solution:

\usetikzlibrary{backgrounds}

\begin{tikzpicture}[
show background rectangle,
declare function={
  f(\x) = \x - sin(deg(\x));
  s(\x) = 0.8;
  xmin = 0;
  xmax = 2*pi;
}]
\foreach \dh/\color in {1/20, 0.5/40, 0.25/60, 0.125/80, 0.0625/100} {
  \fill[smooth,color=red!\color,domain=xmin:xmax] plot (\x,{f(\x)+\dh*s(\x)}) --
     plot[domain=xmax:xmin] (\x,{f(\x)-\dh*s(\x)}) -- cycle;
}
\node at (current bounding box.south east) {$m$};
\node at (current bounding box.north west) {$d$};
\end{tikzpicture}

enter image description here

Unfortunately, PGFPlots doesn't allow cycle f(x)+s(x) and f(x)-s(x) with \addplot as I did with the TikZ \draw command. Improvements are welcome.

Community
  • 1
juliohm
  • 3,452
  • @Jake, feel free to edit my answer towards the desired solution. – juliohm Oct 22 '13 at 16:48
  • 1
    You can use the count and evaluate functionalities of \foreach: \foreach \dh [count=\i, evaluate=\i as \colorfactor using \i*20] in {1,0.5,0.25,0.125,0.0625} { \draw[fill=red!\colorfactor, domain=xmin:xmax] plot (\x,{f(\x)+\dh*s(\x)}) -- plot[domain=xmax:xmin] (\x,{f(\x)-\dh*s(\x)}) -- cycle; } – Jake Oct 24 '13 at 16:04
  • @Jake, almost there, could you please give a hint on how to fit the axis environment to the drawing? – juliohm Oct 24 '13 at 16:40
  • You can make the axis and the path use the same coordinate system by using \begin{axis}% [anchor=origin, x=1cm, y=1cm,xlabel={$m$},ylabel={$d$}, xmin=0, xmax=2*pi, ymin=-1, ymax=8] \end{axis}. I don't think this is a good idea at all, though: With this approach, you're basically losing all the advantages that PGFPlots brings with it (automatic scaling, automatic axis limits, automatic legends). – Jake Oct 24 '13 at 16:49
  • @Jake, how would you insert the axis or use \addplot command directly? I wasn't able to cycle top and bottom curves with \addplot, that is why I did it with \draw commands. – juliohm Oct 24 '13 at 16:54
  • I know, you can't just reverse the paths in PGFPlots. Hence the more complicated but more general (also works with tabulated data, for instance) approach in my answer. stack plots together with \closedcycle is meant for exactly that purpose. – Jake Oct 24 '13 at 16:59
  • @Jake, the output for stack plots in your answer has some visible rounding errors, see the mean function isn't equidistant from the upper/lower bounds. – juliohm Oct 24 '13 at 17:07
  • let us continue this discussion in chat – Jake Oct 24 '13 at 17:21
2

A recommended solution with PSTricks.

\documentclass[pstricks,border=12pt]{standalone}
\usepackage{pst-plot}

\def\f(#1,#2){#1-sin(#1)+.8*(#2)}

\psset{algebraic,fillstyle=solid}

\begin{document}
\begin{pspicture}(-1,-1)(8,8)
\foreach \dh/\color in {1/20, 0.5/40, 0.25/60, 0.125/80, 0.0625/100} 
{
    \pscustom[fillcolor=red!\color,linestyle=none]
    {
        \psplot{0}{Pi 2 mul}{\f(x,\dh)}
        \psplot{Pi 2 mul}{0}{\f(x,-\dh)}
        \closepath
    }
}
\psaxes{->}(0,0)(-1,-1)(7.5,7.5)[$x$,0][$y$,90]
\rput[tl](-1,8){$d$}
\rput[br](8,-1){$m$}
\end{pspicture}
\end{document}

enter image description here

kiss my armpit
  • 36,086