This is not new with respect to other answers, but I'd like to introduce a couple of tricks:
\documentclass{article}
\usepackage{amsmath,mathtools}
\usepackage{amssymb}
\newcommand{\V}[1]{\mathrm{#1}} % or \mathit
\newcommand{\numberset}[1]{\mathbb{#1}}
\newcommand{\R}{\numberset{R}}
\begin{document}
This is the original equation
\begin{equation}
RA_{U}(\V{new},\V{ref}) =
\bigcup_{
\quad
\mathclap{\substack{
\text{$i$ such that}\\[\jot]
f_i(\V{ref}) < f_i(\V{new})
}}
\quad
}
\{
X \in \R^{M} :
x_i \in [f_i(\V{ref}); f_i(\V{new})]
\}
\end{equation}
\renewcommand{\V}[1]{\mathit{#1}}
\renewcommand{\numberset}[1]{\mathsf{#1}}
Just to see the effect of changing just a couple of commands
\begin{equation}
RA_{U}(\V{new},\V{ref}) =
\bigcup_{
\quad
\mathclap{\substack{
\text{$i$ such that}\\[\jot]
f_i(\V{ref}) < f_i(\V{new})
}}
\quad
}
\{
X \in \R^{M} :
x_i \in [f_i(\V{ref}); f_i(\V{new})]
\}
\end{equation}
\end{document}
The main trick is the macro \V for typesetting multiletter variables; then also \numberset is defined, which is used indirectly for defining \R (and other number sets). I show how, just changing those definitions, one can change the output.
For the wide subscript I use \substack in a \mathclap, but adding some space around it in order that the union symbol is not adjacent to its surroundings.
Note the \jot used for giving some room between the two lines in the subscript. Also \text{$i$ such that} is handier to type than i\text{ such that}, because spaces are ‘natural’.



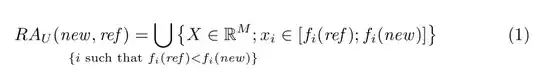

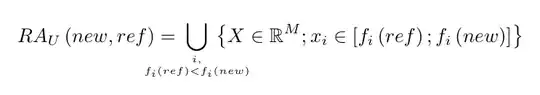

cmex10option foramsmath; it's just for compatibility with *very old* TeX distributions. – egreg Nov 22 '13 at 16:50$X=(x_1,x_2,...x_m)$? If so, you are quantifying over$i$twice, once in the\bigcupand again in the set to its right. This is a mathematical error. – Dan Nov 23 '13 at 03:49f_i(ref) < f_i(old)below the\bigcupsince i is the only free variable. – Caramdir Nov 23 '13 at 17:18