Modiagram Package: How can we add 3s,3d ... orbitals?

Question

I'm learning to use LaTeX to prepare my chemistry lessons using Beamer. While searching the internet I found the modiagram package that helped me so much, but I need help with the following:

How can I build energy diagrams for individual atoms? I would like to be able to add the 3s, 3d, etc. orbitals
Also, how can I put energy values on the y axis, like hidrogen energy level's diagram?

Have you tried anything so far? If you have a minimal compilable document showing what you've done to try to produce the result then people will be able to help you faster and better. See minimal working example (MWE) for what needs to go into such a document. — Adam Liter, Nov 25 '13 at 03:05
Also, Welcome to TeX.SX! :-) You might want to have a look at our starter guide to familiarize yourself further with our format. Generally, it's best to mark package names with ``` backticks to make them stand out. We also generally avoid using names in posts since it automatically appears in the lower right corner of your post. Welcome! — Adam Liter, Nov 25 '13 at 03:26
d-Orbitals are not implemented... and neither is an energy axis with values, I'm afraid. You can have a look at Molecular orbital diagrams in LaTeX? for alternatives to modiagram — cgnieder, Nov 25 '13 at 09:27

score 8 · Accepted Answer · answered Jan 11 '14 at 17:46

While the modiagram package does not cover a full range of orbitals, it is still worth using in concert with lower-level TikZ directives for constructing more involved cases. I have used the package in illustrating crystal field theory; for example, the case of a pure sigma donor might look like:

\documentclass{article}
\usepackage{modiagram}
\usepackage{upgreek}
\begin{document}

\begin{figure}
  \centering
    \begin{MOdiagram}[lines = gray]
      \small
      % Metal
      \AO[metal-3d-1]{s}{-0.10;}
      \AO[metal-3d-2]{s}{-0.05;}
      \AO[metal-3d-3]{s}{ 0.00;}
      \AO[metal-3d-4]{s}{ 0.05;}
      \AO[metal-3d-5]{s}{ 0.10;}
      % Complex
      \AO[complex-t2g-1](50 pt){s}{-1.05;}
      \AO[complex-t2g-2](50 pt){s}{-1.00;}
      \AO[complex-t2g-3](50 pt){s}{-0.95;}
      \AO[complex-eg-1] (50 pt){s}{1.50;}
      \AO[complex-eg-2] (50 pt){s}{1.55;}

      \node[inner sep = 0, outer sep = 0]
        (midway) at (55 pt, 0 pt) {};
      \draw[style = dotted] (45 pt, 0 pt) --  ++ (10 pt, 0 pt);

      \connect{
        metal-3d-3 & complex-t2g-2,
        metal-3d-3 & complex-eg-1
      }
      \node[right] at (complex-t2g-1.east){$\mathrm{t}_{2\mathrm{g}}$};
      \node[right] at (complex-eg-1.east) {$\mathrm{e}_{\mathrm{g}}$};

      \draw[orange, <->] (complex-t2g-3.west) -- (complex-eg-1.west)
        node[midway,left] {$\Delta_{\mathrm{O}}$} ;
      \draw[orange, <->] (complex-eg-1.east) -- (midway.east)
        node[midway,right] {$\frac{3}{5}\Delta_{\mathrm{O}}$} ;
      \draw[orange, <->] (complex-t2g-3.east) -- (midway.east)
        node[midway,right] {$\frac{2}{5}\Delta_{\mathrm{O}}$} ;
    \end{MOdiagram}
  \caption{Octahedral field splitting}
\end{figure}

\begin{figure}
  \centering
  \begin{MOdiagram}[lines= gray]
    \small
    % Metal
    \AO[metal-3d-1]{s}{3.20;}
    \AO[metal-3d-2]{s}{3.25;}
    \AO[metal-3d-3]{s}{3.30;}
    \AO[metal-3d-4]{s}{3.35;}
    \AO[metal-3d-5]{s}{3.40;}
    \AO[metal-4s]  {s}{5.00;}
    \AO[metal-4p-1]{s}{5.65;}
    \AO[metal-4p-2]{s}{5.70;}
    \AO[metal-4p-3]{s}{5.75;}

    % Ligand
    \AO[ligand-1](100 pt){s}{2.00;}
    \AO[ligand-2](100 pt){s}{2.05;}
    \AO[ligand-3](100 pt){s}{2.10;}
    \AO[ligand-4](100 pt){s}{2.15;}
    \AO[ligand-5](100 pt){s}{2.20;}
    \AO[ligand-6](100 pt){s}{2.25;}

    % Complex
    \AO[complex-a1g]   (50 pt){s}{0.30;}
    \AO[complex-t1u-1] (50 pt){s}{0.75;}
    \AO[complex-t1u-2] (50 pt){s}{0.80;}
    \AO[complex-t1u-3] (50 pt){s}{0.85;}
    \AO[complex-eg-1]  (50 pt){s}{1.40;}
    \AO[complex-eg-2]  (50 pt){s}{1.45;}
    \AO[complex-t2g-1] (50 pt){s}{3.25;}
    \AO[complex-t2g-2] (50 pt){s}{3.30;}
    \AO[complex-t2g-3] (50 pt){s}{3.35;}
    \AO[complex-eg*-1] (50 pt){s}{4.30;}
    \AO[complex-eg*-2] (50 pt){s}{4.35;}
    \AO[complex-a1g*]  (50 pt){s}{6.00;}
    \AO[complex-t1u*-1](50 pt){s}{6.35;}
    \AO[complex-t1u*-2](50 pt){s}{6.40;}
    \AO[complex-t1u*-3](50 pt){s}{6.45;}

    \connect
      {
        metal-3d-3     & complex-eg-1  ,
        metal-3d-3     & complex-t2g-2 ,
        metal-3d-3     & complex-eg*-1 ,
        metal-4s       & complex-a1g   ,
        metal-4s       & complex-a1g*  ,
        metal-4p-2     & complex-t1u-2 ,
        metal-4p-2     & complex-t1u*-2,
        complex-a1g    & ligand-3      ,
        complex-a1g*   & ligand-3      ,
        complex-t1u-2  & ligand-3      ,
        complex-t1u*-2 & ligand-3      ,
        complex-eg-1   & ligand-3      ,
        complex-eg*-1  & ligand-3
      }

    \node[left] at (metal-3d-3.west) {$n\mathrm{d}$};
    \node[left] at (metal-4s.west)   {$(n + 1)\mathrm{s}$};
    \node[left] at (metal-4p-1.west) {$(n + 1)\mathrm{p}$};

    \node[below] at (complex-a1g)   {$\mathrm{a}_{1\mathrm{g}}$};
    \node[below] at (complex-t1u-1) {$\mathrm{t}_{1\mathrm{u}}$};
    \node[below] at (complex-eg-1)  {$\mathrm{e}_{\mathrm{g}}$};
    \node[below] at (complex-t2g-1) {$\mathrm{t}_{2\mathrm{g}}$};
    \node[above] at (complex-eg*-1) {$\mathrm{e}_{\mathrm{g}}*$};
    \node[below] at (complex-a1g*.south)  {$\mathrm{a}_{1\mathrm{g}}*$};
    \node[above] at (complex-t1u*-1.north){$\mathrm{t}_{1\mathrm{u}}*$};

    \node[right] at (ligand-3.east) {$\upsigma$};

    \draw[orange, <->] (complex-t2g-3.center) -- (complex-eg*-1.center)
      node[midway,left] {$\Delta_{\mathrm{O}}$} ;

    \node at (  0 pt, -20 pt) {Metal};
    \node at ( 50 pt, -20 pt) {Complex};
    \node at (100 pt, -20 pt) {Ligands};
  \end{MOdiagram}
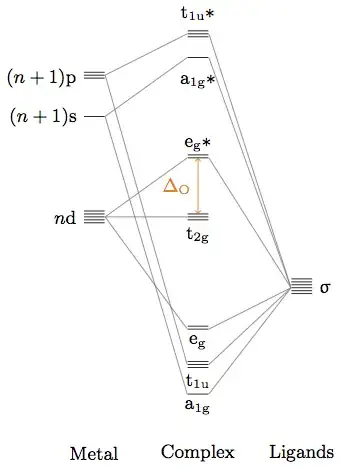
  \caption{Octahedral splitting with a pure $\upsigma$-donor}
\end{figure}

\end{document}

enter image description here

Modiagram Package: How can we add 3s,3d ... orbitals?

1 Answers1

Linked