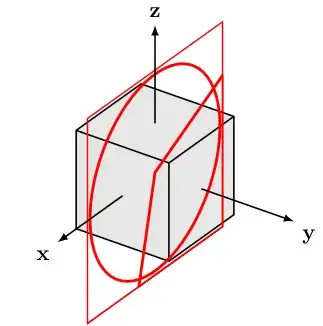
In the following code, I'm trying to draw three clipped circles in three orthogonal planes. I'm using this approach to clip the appropriate sections of the circles. This works nicely in the xy and yz planes, but not in the xz plane, as shown in the output.

Based on the output, it seems I have made a simple mistake, but I just can't find it. I've tried checking the coordinates in the scope for the xz plane (red circle), and they appear to be correct. I've attached three figures which show the clipping paths for each scope. (The drawn clipping paths show some minor inaccuracies, but these are irrelevant to the problem.) Any help finding the error would be much appreciated.
Some mathematical properties which might make the code clearer:
- The center of the box is the point (1,1,1)
- The drawn axes meet at (1,1,1), not the origin, so the figure is essentially shifted [1,1,1]
- All the circles are concentric with center point (1,1,1)
- The radius of the circles is 2
\documentclass[11pt]{standalone}
\usepackage[utf8]{inputenc}
\usepackage{tikz,tikz-3dplot}
\usetikzlibrary{arrows}
\begin{document}
\definecolor{darkgreen}{rgb}{0.1,0.7,0.1}
\tdplotsetmaincoords{60}{125}
\begin{tikzpicture}[tdplot_main_coords,>=latex]
\pgfsetlinewidth{0.8}
\tdplotsetcoord{P}{3.4641}{54.74}{45}
% box
\draw[fill=black!10] (Px) -- (Pxy) -- (Py) -- (Pyz) -- (Pz) -- (Pxz) -- cycle;
\draw (Pxy) -- (P);
\draw (Pxz) -- (P);
\draw (Pyz) -- (P);
\pgfsetlinewidth{1.4}
\begin{scope} % blue circle, xy plane
\color{blue}
\tikzstyle{reverseclip}=[insert path={(3.1,3.1,1) -- (-1.1,3.1,1) -- (-1,-1.1,1) -- (3.1,-1.1,1) -- (3.1,3.1,1)}]
\begin{pgfinterruptboundingbox}
\path[clip] (1,1,1) -- (1.3,-1.1,1) -- (-1.1,-1.1,1) -- (-1.1,2,1) -- cycle [reverseclip];
\end{pgfinterruptboundingbox}
\pgfpathellipse{\pgfpointxyz{1}{1}{1}}{\pgfpointxyz{2}{0}{0}}{\pgfpointxyz{0}{2}{0}}
\pgfusepath{draw}
\end{scope}
\begin{scope} % green circle, yz plane
\color{darkgreen}
\tikzstyle{reverseclip}=[insert path={(1,3.1,3.1) -- (1,3.1,-1.1) -- (1,-1.1,-1.1) -- (1,-1.1,3.1) -- (1,3.1,3.1)}]
\begin{pgfinterruptboundingbox}
\path[clip] (1,1,1) -- (1,-1.1,1.8) -- (1,-1.1,-1.1) -- (1,1.7,-1.1) -- cycle [reverseclip];
\end{pgfinterruptboundingbox}
\pgfpathellipse{\pgfpointxyz{1}{1}{1}}{\pgfpointxyz{0}{2}{0}}{\pgfpointxyz{0}{0}{2}}
\pgfusepath{draw}
\end{scope}
\begin{scope} % red circle, xz plane
\color{red}
\tikzstyle{reverseclip}=[insert path={(3.1,1,3.1) -- (-1.1,1,3.1) -- (-1.1,1,-1.1) -- (3.1,1,-1.1) -- (3.1,1,3.1)}]
\begin{pgfinterruptboundingbox}
\path[clip] (1,1,1) -- (-1.1,1,2) -- (-1.1,1,-1.1) -- (1.5,1,-1.1) -- cycle [reverseclip];
\end{pgfinterruptboundingbox}
\pgfpathellipse{\pgfpointxyz{1}{1}{1}}{\pgfpointxyz{2}{0}{0}}{\pgfpointxyz{0}{0}{2}}
\pgfusepath{draw}
\end{scope}
% axes
\draw[line width=0.8pt,->] (2,1,1) -- (4,1,1) node[anchor=north east]{\textbf{x}};
\draw[line width=0.8pt,->] (1,2,1) -- (1,4,1) node[anchor=north west]{\textbf{y}};
\draw[line width=0.8pt,->] (1,1,2) -- (1,1,4) node[anchor=south]{\textbf{z}};
\end{tikzpicture}
\end{document}





pgf. I found out I had an outdated version ofpgf, so I updated it, and now I, too, get output with a cropped bottom. I don't know why. If anyone happens to read this and know the answer, please do leave a comment. – eiterorm May 17 '14 at 20:44standalone? – cfr May 17 '14 at 20:52pathanddrawcommands were supposed to increase the size of the canvas. They did before. – eiterorm May 17 '14 at 20:55\node at (2,0,-1) {};works. – cfr May 17 '14 at 21:00pgfinterruptboundingbox. Commenting out the box in the last scope makes the entire figure show. This also means that it's only thepathcommand (not thedrawcommand) which expands the canvas. – eiterorm May 17 '14 at 21:03\draw), it all fits. Even if I remove the nodes with anchors and labels so it is just\drawcommands... – cfr May 17 '14 at 21:07draw(on a previously defined path) doesn't seem to expand the canvas (because the expansion is caused by thepathcommand). – eiterorm May 17 '14 at 21:11