Can anyone help please? I need to know how to make the sum of value S(n) = 0+1+2+3+4...+(n-1)+n (example: 0+1+2+3 = 6 , 0+1+2+3+4+5+6+7 = 28 and so on) on Latex
6 Answers
The difficult task is generating the terms of the sequence, not computing the sum, of course; I present a macro that prints all the terms or just the sum. You can define a different starting point and another difference (defaults 0 and 1).
\documentclass{article}
\usepackage{xparse}
\ExplSyntaxOn
\NewDocumentCommand{\arithmeticsequence}{sO{}m}
{
\group_begin:
\keys_set:nn {rudstep/arseq} { #2 }
\IfBooleanTF{#1}
{ \rudstep_arseq_sum:n { #3 } }
{ \rudstep_arseq_full:n { #3 } }
\group_end:
}
\keys_define:nn { rudstep/arseq }
{
diff .int_set:N = \l_rudstep_diff_int,
start .int_set:N = \l_rudstep_start_int,
diff .initial:n = 1,
start .initial:n = 0,
}
\seq_new:N \l_rudstep_terms_seq
\cs_new_protected:Npn \rudstep_arseq_full:n #1
{
\seq_clear:N \l_rudstep_terms_seq
\int_step_inline:nnnn
{ \l_rudstep_start_int } % start
{ \l_rudstep_diff_int } % step
{ \l_rudstep_start_int + #1*\l_rudstep_diff_int } % end
{ \seq_put_right:Nn \l_rudstep_terms_seq { ##1 } }
$\seq_use:Nn \l_rudstep_terms_seq { + } = \rudstep_arseq_sum:n { #1 }$
}
\cs_new:Npn \rudstep_arseq_sum:n #1
{
\int_eval:n { (#1+1)*(2*\l_rudstep_start_int+#1*\l_rudstep_diff_int)/2 }
}
\ExplSyntaxOff
\begin{document}
Just the sum of five terms after 0: \arithmeticsequence*{5}
The whole sequence: \arithmeticsequence{3}
Or: \arithmeticsequence{4}
Start from 1: \arithmeticsequence[start=1]{3}
\bigskip
A big example:
\arithmeticsequence[start=81297,diff=198]{180}
\end{document}

Of course, if you know how to do it in Lisp, then here's the way:
\documentclass{article}
\usepackage{lisp-on-tex}
\begin{document}
\lispinterp{
(\define \intsum
(\lambda (\n)
(\lispif (\= \n :0 ) :0
(\+ (\intsum (\- \n :1)) \n))))}
\lispinterp{(\texprint(\intsum:100))}
\end{document}
that prints, as is well known,
5050
Note: shamelessly adapted from the documentation of lisp-on-tex.
The e-TeX version of the same idea, using recursion, can be
\documentclass{article}
\newcommand{\Sn}[1]{%
\number\numexpr #1
\ifnum\numexpr#1-1>0
+\expandafter\Sn\expandafter{\number\numexpr#1-1}
\fi
\relax
}
\begin{document}
\Sn{10}
\Sn{100}
\end{document}
Note that this is fully expandable. The macro \Sn starts from the argument and if it's bigger than 1 asks to expand \Sn with the argument decreased by 1. One might start also from 0, but I'll leave it as an exercise to the interested reader.
- 1,121,712
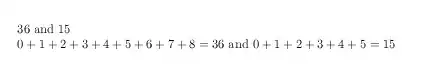
\documentclass{article}
\newcommand\foo[1]{\the\numexpr((#1)*(#1+1))/2\relax}
% or if you want to print the terms
\newcommand\foob[1]{$\fooc{#1}{0}=\foo{#1}$}
\newcommand\fooc[2]{\the\numexpr#2\relax\ifnum#1=#2\relax\else+\fooc{#1}{\numexpr#2+1\relax}\fi}
\begin{document}
\foo{8} and \foo{5}
\foob{8} and \foob{5}
\end{document}
- 757,742
-
-
@rudstep loads of solutions to that already: http://tex.stackexchange.com/search?q=Fibonacci – David Carlisle Sep 18 '14 at 15:23
-
can you please please explain me the codes you gave me for the SUM of value n. – rudstep Sep 18 '14 at 15:45
-
@rudstep \numexpr is an (e-)tex primitive to do numerical calculations, and (n)(n+1)/2 is the well known formula for the sum of the integers up to n – David Carlisle Sep 18 '14 at 15:54
-
Mister David Carliste thank you so much for your help. This help me a lot. but i don't understand the fibonacci on the link you sent me. – rudstep Sep 18 '14 at 16:09
-
@rudstep The link does a search of the site and shows up previous questions about Fibonacci-related problems. Probably one or other of them will be helpful. – Joseph Wright Sep 18 '14 at 16:13
-
of course this provides the correct numerical answer, but if it's also required to print the complete sequence that sums to the result, then more is necessary. (i could accuse you of being lazy if i didn't know better. devious, definitely; lazy, no.) – barbara beeton Sep 18 '14 at 16:26
-
@barbarabeeton yes the question wasn't clear on that (a bit more would be necessary, but not necessarily a long biographical treatise on Gauss:-) – David Carlisle Sep 18 '14 at 16:28
-
1
Using Lua is probably a huge overkill in this situation, but it shows off how one can easily integrate Lua in LaTeX.
The code might also be easier to grasp for programmers who are beginners in LaTeX ;)

% !TEX TS-program = lualatex
% !TEX encoding = UTF-8 Unicode
\documentclass{article}
\usepackage[utf8]{luainputenc}
\usepackage{luacode}
% The code won't work as-is if you move it into \directlua{}.
% If you do so, be sure to replace "~" (in i ~= startInt) by \string~
\begin{luacode}
function calcSum(startInt, endInt)
local sum = 0
for i=startInt, endInt do
sum = sum + i
end
return sum
end
function writeSum(startInt, endInt)
local sum = 0
local tex = ""
for i=startInt, endInt do
if i ~= startInt then
tex = tex .. " + "
end
sum = sum + i
tex = tex .. i
end
tex = tex .. " = " .. sum
return tex
end
\end{luacode}
\def\calcSum#1#2{\directlua{
tex.print(calcSum(tonumber(#1), tonumber(#2)))
}}
\def\writeSum#1#2{\directlua{
tex.print(writeSum(tonumber(#1), tonumber(#2)))
}}
\begin{document}
\noindent
The sum of the numbers \(0, 1, 2, \ldots, 28\) is \(\calcSum{0}{28}\).\\
Another sum: \(\writeSum{100}{103}\).
\end{document}
- 1,248
- 2
- 15
- 22
-
May be
\string~would work? Remember that everything is expanded (IIRC) before passing to Lua. – Manuel Sep 18 '14 at 20:01 -
@Manuel Thanks, that did the trick! That's also one of the reasons that one should use external .lua files, I guess. – ComFreek Sep 18 '14 at 20:52
-
Or, at least, something more “prepared” than
\directlua. I thinkluacodepackage offers some advances. In ConTeXt they have an environment where\n,\t,~, etc. needn't to be escaped since it's defined to work (I think that's whatluacodedoes in LaTeX). – Manuel Sep 18 '14 at 20:55 -
@Manuel LuaLaTeX says that
the environment luacode* [is] undefined. I'll investigate tomorrow. – ComFreek Sep 18 '14 at 21:09 -
With
luacodepackage, you have\luaexec,luacodeenvironment, andluacode*environment. – Manuel Sep 18 '14 at 21:12 -
Here is a short expl3 approach using \int_step_inline:nnnn. This carries out the explicit sum and doesn't rely on Gauss' reduction. So this is for illustration purposes only.
\documentclass{article}
\usepackage{xparse}
\ExplSyntaxOn
\cs_generate_variant:Nn \int_to_arabic:n { V }
\cs_new:Npn \rudstep_sum:n #1
{
\int_zero:N \l_tmpa_int
\int_step_inline:nnnn { 1 } { 1 } { #1 }
{
\int_add:Nn \l_tmpa_int { ##1 }
}
\int_to_arabic:V \l_tmpa_int
}
\NewDocumentCommand \calcsum {m}
{
\rudstep_sum:n { #1 }
}
\ExplSyntaxOff
\begin{document}
\calcsum{8}
\end{document}
- 109,596
Using my package calculator, you can perform arithmetic calculations comfortably. This code solves your problem:
\documentclass{article}
\usepackage{ifthen}
\usepackage{calculator}
\newcounter{n}
\newcommand{\sumZeroToN}[2]{%
\COPY{0}{#2}
\whiledo{\not{\value{n}>#1}}{%
\ADD{#2}{\value{n}}{#2}\stepcounter{n}}}
\begin{document}
\sumZeroToN{100}{\sol}
\[
\sum_{n=0}^{100} n = \sol
\]
\end{document}
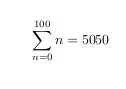
- 1,151
-
That's cool, but it would be nice to see a solution without
ifthenand which can calculate more than\sumZeroToN{181}{\sol}. If you have time, you could try that. It would also be nice to set the power just once.\sum_{n=0}^{\power}. – LaRiFaRi Sep 19 '14 at 08:06
An expandable solution using the package bnumexpr for computations and \xintiloop for expandably looping with an index.
\documentclass{article}
\usepackage{bnumexpr}% minimally extends \numexpr to big integers (new on CTAN
% as of 2014/09/22)
% for \xintiloop: (for fun)
\usepackage{xinttools}% automatically loaded by xint, which is loaded by
% bnumexpr, but in the future bnumexpr will only load a
% smaller part of xint, and xint itself will not load
% xinttools anymore.
\newcommand{\ArithmeticSequenceAndItsSum}[3]{%
% #1= initial term, A
% #2= common difference, d
% #3= number of terms, N
% sum is A+(A+d)+...+(A+(N-1)d)=N*A+d*N(N-1)/2
% (cf. Gauss Werke, Kindergarten Abteilung)
%
#1% assume N at least one and that #1 does not need to be evaluated
\xintiloop [1+1]
\unless\ifnum#3=\xintiloopindex
+\thebnumexpr#1+\xintiloopindex*#2\relax
\repeat
=\thebnumexpr #3*#1+#2*#3*(#3-1)/2\relax
}
\begin{document}
$\ArithmeticSequenceAndItsSum {0}{1}{10}$
$\ArithmeticSequenceAndItsSum {1}{2}{10}$
\noindent $\ArithmeticSequenceAndItsSum {111111111}{111111111}{100}$
And now go see the log for some bigger integers!!
\message{\ArithmeticSequenceAndItsSum {123456789}{987654321}{1000}}
\end{document}

$0+1+2+3=6$would work) or you want latex do do the calculation or...? – David Carlisle Sep 18 '14 at 14:53\sum\limits^{3}_{k=0} kwould be the shortest ;-) Perhaps there is even some version using Einstein's convention ;-) – Sep 18 '14 at 17:23n*(n+1)/2is the nth triangular number. The nth triangular number is yourS(n). (this is perhaps most useful if you only need to show the end result, not the0+1+2+...part) – Tim S. Sep 18 '14 at 23:53