Count the number of elements of each size in a list

Question

Comment: The following question is somewhat similar to "Position of largest element in a list" but I'm (unfortunately) not familiar what LaTeX 3 programming so I'm forced to ask. :(

Code: Consider the following example:

\documentclass{beamer}

\usepackage[danish]{babel}
\usepackage[utf8]{inputenc}
\usepackage[T1]{fontenc}
\usepackage{lmodern}
\usepackage{booktabs}
\usepackage{siunitx}

\begin{document}

\def\elevA{6}
\def\elevB{0}
\def\elevC{0}
\def\elevD{3}
\def\elevE{0}
\def\elevF{2}
\def\elevG{1}
\def\elevH{1}
\def\elevI{1}
\def\elevJ{5}
\def\elevK{0}
\def\elevL{3}
\def\elevM{7}
\def\elevN{3}
\def\elevO{1}
\def\elevP{1}
\def\elevQ{0}
\def\elevR{0}
\def\elevS{0}
\def\elevT{2}
\def\elevU{1}
\def\elevV{2}
\def\elevW{0}
\def\elevX{2}
\def\elevY{1}
\def\elevZ{1}
\def\elevAa{4}
\def\elevAb{6}
\def\elevAc{1}
\def\elevAd{1}
\def\elevAe{6}
\def\elevAf{2}
\def\elevAg{0}
\def\elevAh{3}
\def\elevAi{2}
\def\elevAj{1}
\def\elevAk{0}
\def\elevAl{0}
\def\elevAm{0}
\def\elevAn{0}
\def\elevAo{0}
\def\elevAp{4}

\begin{frame}

\begin{table}
\centering
\small
  \begin{tabular}{*{14}{c}}
   \toprule
    \elevA  & \elevB  & \elevC  & \elevD  & \elevE  & \elevF  & \elevG  &
    \elevH  & \elevI  & \elevJ  & \elevK  & \elevL  & \elevM  & \elevN    \\[0.5ex]
    \elevO  & \elevP  & \elevQ  & \elevR  & \elevS  & \elevT  & \elevU  &
    \elevV  & \elevW  & \elevX  & \elevY  & \elevZ  & \elevAa & \elevAb   \\[0.5ex]
    \elevAc & \elevAd & \elevAe & \elevAf & \elevAg & \elevAh & \elevAi &
    \elevAj & \elevAk & \elevAl & \elevAm & \elevAn & \elevAo & \elevAp   \\
   \bottomrule
  \end{tabular}
\end{table}
\end{frame}

\end{document}

Output:

output

Question: How do I make LaTeX count the number of entries with each value (here it's 0, 1, ..., 7)? What I mean is, how many times in the list does a 0 occur, how many times in the list does a 1 occur and so forth.

If a macro like \HowMany can be created and then use, say, \HowMany{0} with the reture value 14, it will be really nice!

Notes:

It doesn't have to be a LaTeX 3 solution, but I need to compile the original document (i.e., the one I need the solution for) via latex --> dvips --> ps2pdf.
The input numbers are via the \def method.
I can find the minimum value (here it's 0) and maximum value (here it's 7) myself but if LaTeX can do it, it will (of course) be preferable.

Sorry, is there no better method other than use a bunch of \def... macros? How about a 'real' list? And are the values integers only? — , Mar 15 '15 at 11:42
@SoundsOfSilence The point is that I have to use the numbers in several places in my 'real' document so I've really like to make it as automatic as possible (and try to minimize the risk of making typos when I use the same numbers again). — Svend Tveskæg, Mar 15 '15 at 11:43
Please, be more specific on how and where the number of matches should be used. — egreg, Mar 15 '15 at 12:02
@egreg Question updated. I hope it's specific enough; otherwise, let me know and I'll try to reformulate. — Svend Tveskæg, Mar 15 '15 at 12:13
@egreg Q updated again. Sorry for not doing it properly in the first update. — Svend Tveskæg, Mar 15 '15 at 12:20

egreg · Accepted Answer · 2015-03-15T14:08:21.243

A more complicated approach, showing how giving more structure to your macros can give less problems.

Instead of several \elevXY macros, I define just one that takes the letters as argument. The corresponding values are stored in a property list.

The standard behavior of \elev is to print the corresponding number (in this incarnation it is fully expandable). However, after the \countappearances declaration, besides printing the number it will update another property list storing the number of appearances until then. This property list is initialized to store 0 for each number. The declaration is local, so its effects will vanish as soon as the table (or frame environment, if table is not used) ends.

Finally, \HowMany accesses the property corresponding to the number. The values are stored in the counting property list in a global fashion, so they'll be accessible until the next \countappearances declaration.

\documentclass{beamer}

\usepackage[danish]{babel}
\usepackage[utf8]{inputenc}
\usepackage[T1]{fontenc}
\usepackage{lmodern}
\usepackage{booktabs}
\usepackage{siunitx}
\usepackage{xparse}

\ExplSyntaxOn
\prop_new:N \g_svend_elev_prop
\prop_gput:Nnn \g_svend_elev_prop {A} {6}
\prop_gput:Nnn \g_svend_elev_prop {B} {0}
\prop_gput:Nnn \g_svend_elev_prop {C} {0}
\prop_gput:Nnn \g_svend_elev_prop {D} {3}
\prop_gput:Nnn \g_svend_elev_prop {E} {0}
\prop_gput:Nnn \g_svend_elev_prop {F} {2}
\prop_gput:Nnn \g_svend_elev_prop {G} {1}
\prop_gput:Nnn \g_svend_elev_prop {H} {1}
\prop_gput:Nnn \g_svend_elev_prop {I} {1}
\prop_gput:Nnn \g_svend_elev_prop {J} {5}
\prop_gput:Nnn \g_svend_elev_prop {K} {0}
\prop_gput:Nnn \g_svend_elev_prop {L} {3}
\prop_gput:Nnn \g_svend_elev_prop {M} {7}
\prop_gput:Nnn \g_svend_elev_prop {N} {3}
\prop_gput:Nnn \g_svend_elev_prop {O} {1}
\prop_gput:Nnn \g_svend_elev_prop {P} {1}
\prop_gput:Nnn \g_svend_elev_prop {Q} {0}
\prop_gput:Nnn \g_svend_elev_prop {R} {0}
\prop_gput:Nnn \g_svend_elev_prop {S} {0}
\prop_gput:Nnn \g_svend_elev_prop {T} {2}
\prop_gput:Nnn \g_svend_elev_prop {U} {1}
\prop_gput:Nnn \g_svend_elev_prop {V} {2}
\prop_gput:Nnn \g_svend_elev_prop {W} {0}
\prop_gput:Nnn \g_svend_elev_prop {X} {2}
\prop_gput:Nnn \g_svend_elev_prop {Y} {1}
\prop_gput:Nnn \g_svend_elev_prop {Z} {1}
\prop_gput:Nnn \g_svend_elev_prop {Aa} {4}
\prop_gput:Nnn \g_svend_elev_prop {Ab} {6}
\prop_gput:Nnn \g_svend_elev_prop {Ac} {1}
\prop_gput:Nnn \g_svend_elev_prop {Ad} {1}
\prop_gput:Nnn \g_svend_elev_prop {Ae} {6}
\prop_gput:Nnn \g_svend_elev_prop {Af} {2}
\prop_gput:Nnn \g_svend_elev_prop {Ag} {0}
\prop_gput:Nnn \g_svend_elev_prop {Ah} {3}
\prop_gput:Nnn \g_svend_elev_prop {Ai} {2}
\prop_gput:Nnn \g_svend_elev_prop {Aj} {1}
\prop_gput:Nnn \g_svend_elev_prop {Ak} {0}
\prop_gput:Nnn \g_svend_elev_prop {Al} {0}
\prop_gput:Nnn \g_svend_elev_prop {Am} {0}
\prop_gput:Nnn \g_svend_elev_prop {An} {0}
\prop_gput:Nnn \g_svend_elev_prop {Ao} {0}
\prop_gput:Nnn \g_svend_elev_prop {Ap} {4}

\prop_new:N \g_svend_count_prop
\prop_new:N \g_svend_count_zero_prop
\prop_gput:Nnn \g_svend_count_zero_prop { 0 } { 0 }
\prop_gput:Nnn \g_svend_count_zero_prop { 1 } { 0 }
\prop_gput:Nnn \g_svend_count_zero_prop { 2 } { 0 }
\prop_gput:Nnn \g_svend_count_zero_prop { 3 } { 0 }
\prop_gput:Nnn \g_svend_count_zero_prop { 4 } { 0 }
\prop_gput:Nnn \g_svend_count_zero_prop { 5 } { 0 }
\prop_gput:Nnn \g_svend_count_zero_prop { 6 } { 0 }
\prop_gput:Nnn \g_svend_count_zero_prop { 7 } { 0 }
\prop_gset_eq:NN \g_svend_count_prop \g_svend_count_zero_prop

\tl_new:N \l_svend_number_tl
\tl_new:N \l_svend_count_tl

\DeclareExpandableDocumentCommand{\elev}{m}
 {
  \svend_get_item:n { #1 }
 }

\NewDocumentCommand{\countappearances}{}
 {
  % now \elev will also count
  \cs_set_eq:NN \elev \svend_get_item_count:n
  % reinitialize the counter property list
  \prop_set_eq:NN \g_svend_count_prop \g_svend_count_zero_prop
 }

\DeclareExpandableDocumentCommand{\HowMany}{m}
 {
  \prop_item:Nn \g_svend_count_prop { #1 }
 }

\cs_new:Npn \svend_get_item:n #1
 {
  \prop_item:Nn \g_svend_elev_prop { #1 }
 }

\cs_new_protected:Npn \svend_get_item_count:n #1
 {
  \tl_set:Nx \l_svend_number_tl { \svend_get_item:n { #1 } }
  % print the entry
  \tl_use:N \l_svend_number_tl
  % get the current count
  \tl_set:Nx \l_svend_count_tl
   {
    \prop_item:NV \g_svend_count_prop \l_svend_number_tl
   }
  % advance the count by 1
  \tl_set:Nx \l_svend_count_tl { \int_to_arabic:n { \l_svend_count_tl + 1 } }
  % update the property
  \prop_gput:NVV \g_svend_count_prop \l_svend_number_tl \l_svend_count_tl
 }

\cs_generate_variant:Nn \prop_item:Nn { NV }
\cs_generate_variant:Nn \prop_gput:Nnn { NVV }

\ExplSyntaxOff

\begin{document}

\begin{frame}

\begin{table}
\centering
\small
\countappearances

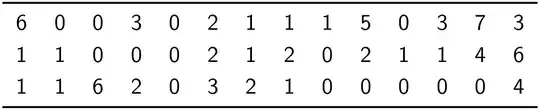
\begin{tabular}{*{14}{c}}
\toprule
\elev{A}  & \elev{B}  & \elev{C}  & \elev{D}  & \elev{E}  & \elev{F}  & \elev{G}  &
\elev{H}  & \elev{I}  & \elev{J}  & \elev{K}  & \elev{L}  & \elev{M}  & \elev{N}    \\[0.5ex]
\elev{O}  & \elev{P}  & \elev{Q}  & \elev{R}  & \elev{S}  & \elev{T}  & \elev{U}  &
\elev{V}  & \elev{W}  & \elev{X}  & \elev{Y}  & \elev{Z}  & \elev{Aa} & \elev{Ab}   \\[0.5ex]
\elev{Ac} & \elev{Ad} & \elev{Ae} & \elev{Af} & \elev{Ag} & \elev{Ah} & \elev{Ai} &
\elev{Aj} & \elev{Ak} & \elev{Al} & \elev{Am} & \elev{An} & \elev{Ao} & \elev{Ap}   \\
\bottomrule
\end{tabular}

\bigskip

\begin{tabular}{*{8}{c}}
\toprule
\multicolumn{8}{c}{How many} \\
\midrule
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\
\HowMany{0} &
\HowMany{1} &
\HowMany{2} &
\HowMany{3} &
\HowMany{4} &
\HowMany{5} &
\HowMany{6} &
\HowMany{7} \\
\bottomrule
\end{tabular}

\end{table}
\end{frame}

\end{document}

enter image description here

That is really nice! I'll definitely take a closer look at this later today (or tomorrow). — Svend Tveskæg, Mar 15 '15 at 14:05
I really like this approach so I've accepted your answer instead. (Any chance I can have you take a look at this question?) — Svend Tveskæg, Mar 16 '15 at 15:08
@SvendTveskæg I don't mind you unaccepting mine, but I'm heartbroken that you've moved the tick to egreg:-) — David Carlisle, Mar 16 '15 at 16:23
Hi egreg. Any chance I can make you extend your answer to use LaTeX 3 so that I can use the command scheme that I've used in the example? (I'm using the scheme that yor've created here for my new documents but I have some old ones with the 'old' command scheme.) Also: Can I use the \HowMany command without having to print all the values, but just store them via \defs? — Svend Tveskæg, Feb 25 '18 at 21:15
@SvendTveskæg Your way of doing things with \def is wrong. — egreg, Feb 25 '18 at 21:21
I know ... I've adopted your scheme for my newer document, but it's for my old ones, with a lot of defs. :-) — Svend Tveskæg, Feb 25 '18 at 21:35

David Carlisle · Answer 2 · 2015-03-15T12:15:50.933

enter image description here

\documentclass{beamer}

\usepackage[danish]{babel}
\usepackage[utf8]{inputenc}
\usepackage[T1]{fontenc}
\usepackage{lmodern}
\usepackage{booktabs}
\usepackage{siunitx}
\usepackage{array}

\def\zz\ignorespaces#1{%
\expandafter\xdef\csname zz#1\endcsname{%
\expandafter\ifx\csname zz#1\endcsname\relax
1%
\else
\the\numexpr\csname zz#1\endcsname+1\relax
\fi}%
#1}

\begin{document}

\def\elevA{6}
\def\elevB{0}
\def\elevC{0}
\def\elevD{3}
\def\elevE{0}
\def\elevF{2}
\def\elevG{1}
\def\elevH{1}
\def\elevI{1}
\def\elevJ{5}
\def\elevK{0}
\def\elevL{3}
\def\elevM{7}
\def\elevN{3}
\def\elevO{1}
\def\elevP{1}
\def\elevQ{0}
\def\elevR{0}
\def\elevS{0}
\def\elevT{2}
\def\elevU{1}
\def\elevV{2}
\def\elevW{0}
\def\elevX{2}
\def\elevY{1}
\def\elevZ{1}
\def\elevAa{4}
\def\elevAb{6}
\def\elevAc{1}
\def\elevAd{1}
\def\elevAe{6}
\def\elevAf{2}
\def\elevAg{0}
\def\elevAh{3}
\def\elevAi{2}
\def\elevAj{1}
\def\elevAk{0}
\def\elevAl{0}
\def\elevAm{0}
\def\elevAn{0}
\def\elevAo{0}
\def\elevAp{4}

\begin{frame}

\begin{table}
\centering
\small
  \begin{tabular}{
    *{14}{>\zz c}
  }
   \toprule
    \elevA  & \elevB  & \elevC  & \elevD  & \elevE  & \elevF  & \elevG  &
    \elevH  & \elevI  & \elevJ  & \elevK  & \elevL  & \elevM  & \elevN    \\[0.5ex]
    \elevO  & \elevP  & \elevQ  & \elevR  & \elevS  & \elevT  & \elevU  &
    \elevV  & \elevW  & \elevX  & \elevY  & \elevZ  & \elevAa & \elevAb   \\[0.5ex]
    \elevAc & \elevAd & \elevAe & \elevAf & \elevAg & \elevAh & \elevAi &
    \elevAj & \elevAk & \elevAl & \elevAm & \elevAn & \elevAo & \elevAp   \\
   \bottomrule
  \end{tabular}
\end{table}

{\count0=0
\loop
\the\count0:\csname zz\the\count0\endcsname\endgraf
\ifnum\count0<8
\advance\count0 1
\repeat
}
\end{frame}



\end{document}

Cool! It's does exactly what I asked for. Extra: How can I create a command like \HowMany{0} and then have it reture the number of zeroes in the list (here 14)? — Svend Tveskæg, Mar 15 '15 at 12:17
Sorry for unaccepting your answer. I just really like the 'structure' in egreg's approach. — Svend Tveskæg, Mar 16 '15 at 15:10

Count the number of elements of each size in a list

2 Answers2

Linked