Create angle bisectors in TikZ

Question

Suppose we have a triangle ABC of given coordinates. Let AD be its altitude. How can I draw the bisector of angle BCD? I'd like to avoid manual calculation of coordinates. I'd rather not use TKZ-Euclide due to its lack of English documentation.

My minimal working example:

\documentclass[11pt]{article}

\usepackage[T1]{fontenc}
\usepackage[utf8]{inputenc}

\usepackage{mathtools}
\usepackage{tikz}
\usetikzlibrary{positioning,calc,intersections}
\begin{tikzpicture}

\coordinate[label=below left:$C$](C) at (-2,0);
\coordinate[label=below right:$A$](A) at (8,0);
\coordinate[label=above left:$B$] (B) at (0,7);
\coordinate[label=above right:$D$](D) at ($(A)!(C)!(B)$);
\draw (A) -- (B) -- (C) -- cycle;
\draw (C) -- (D);

\end{tikzpicture}

Answer 1

\documentclass[11pt]{article}

\usepackage[T1]{fontenc}
\usepackage[utf8]{inputenc}

\usepackage{xparse}

\usepackage{mathtools}
\usepackage{tikz}
\usetikzlibrary{positioning,calc,intersections}

\usetikzlibrary{through}

\NewDocumentCommand{\bissectrice}{%
    O{}     % drawing options
    mmm     % bissector of mmm
    m       % intersection point between base and bissector
    O{1}O{1}% extended drawing of the bissector
    }{%
    \path[name path=Bis#2#3#4] let
        \p1 = ($(#2) - (#3)$),
        \p2 = ($(#4) - (#3)$),
        \n1 = {veclen(\x1,\y1)} ,
        \n2 = {veclen(\x2,\y2)} ,
        \n3 = {max(\n1,\n2)},
        \p1 = ($(#3)!\n3!(#2)$),
        \p2 = ($(#3)!\n3!(#4)$),
        \p3 = ($(\p1) + (\p2) - (#3)$)
    in
        (#3) -- (\p3) ;

    \path[name path = foo] (#2)--(#4) ;

    \path[name intersections={of=foo and Bis#2#3#4, by=#5}] ;

    \path[#1] ($(#3)!#6!(#5)$) -- ($(#5)!#7!(#3)$) ;
    }

\begin{document}
\begin{tikzpicture}

\coordinate[label=below left:$C$](C) at (-2,0);
\coordinate[label=below right:$A$](A) at (8,0);
\coordinate[label=above left:$B$] (B) at (0,7);
\coordinate[label=above right:$D$](D) at ($(A)!(C)!(B)$);
\draw (A) -- (B) -- (C) -- cycle;
\draw (C) -- (D);

\bissectrice[draw,blue]  {B}{C}{D}{R}[1.1]
\bissectrice[draw,dashed]{D}{B}{C}{S}
\bissectrice[draw,dashed]{C}{D}{B}{T}

\path[name intersections={of=BisBCD and BisDBC, by=O}] ;

\node [draw=red] at (O) [circle through={($(C)!(O)!(B)$)}] {};

\end{tikzpicture}
\end{document}

Old version

\documentclass[11pt]{article}

\usepackage[T1]{fontenc}
\usepackage[utf8]{inputenc}

\usepackage{mathtools}
\usepackage{tikz}
\usetikzlibrary{positioning,calc,intersections}

\newcommand{\bissectrice}[6][]{%
    \path[#1] let
        \p1 = ($(#3)!1cm!(#2)$),
        \p2 = ($(#3)!1cm!(#4)$),
        \p3 = ($(\p1) + (\p2) - (#3)$)
    in
        ($(#3)!#6!(\p3)$) -- ($(\p3)!#5!(#3)$) ;
    }

\begin{document}
\begin{tikzpicture}

\coordinate[label=below left:$C$](C) at (-2,0);
\coordinate[label=below right:$A$](A) at (8,0);
\coordinate[label=above left:$B$] (B) at (0,7);
\coordinate[label=above right:$D$](D) at ($(A)!(C)!(B)$);
\draw (A) -- (B) -- (C) -- cycle;
\draw (C) -- (D);

\bissectrice[draw,red]{B}{C}{D}{1.5}{4}


\end{tikzpicture}
\end{document}

Answer 2

Here's how you would do this with tkz-euclide: \tkzDrawBisector(B,C,D)

\documentclass{standalone}
\usepackage{tkz-euclide}
\usetkzobj{all}

\begin{document}
\begin{tikzpicture}
\tkzInit[xmin=-2,xmax=8,ymin=0,ymax=7]
\tkzClip[space=1]

\tkzDefPoint(8,0){A} 
\tkzDefPoint(0,7){B}
\tkzDefPoint(-2,0){C}

\tkzDefPointBy[projection=onto A--B](C)
\tkzGetPoint{D}

\tkzDrawPolygon(A,B,C)
\tkzDrawSegment(C,D)
\tkzDrawBisector(B,C,D)

\tkzLabelPoints(A)
\tkzLabelPoints[above right](B,D)
\tkzLabelPoints[below left](C)
\end{tikzpicture}
\end{document}

Answer 3

An inline Asymptote version:

% bisect.tex
%
\documentclass{article}
\usepackage[inline]{asymptote}
\usepackage{lmodern}
\begin{document}
\begin{figure}
\centering
\begin{asy}
size(7cm);
pen linePen=deepblue+1.2bp, bisectPen=orange+0.8bp;
pair A,B,C,D,E; real CAB,ACD,BCD;
C=(-2,0); A=(8,0); B=(0,7);
CAB=degrees(C-A)-degrees(B-A);
ACD=90-CAB;
D=extension(A,B,C,rotate(ACD,C)*A);
BCD=degrees(B-C)-degrees(D-C);
E=extension(A,B,C,rotate(BCD/2,C)*D);
draw(C--A--B--C--D,linePen);
draw(C--E,bisectPen);
pair[] node={A,B,C,D,E}; string nodename="ABCDE";
pair[] nodepos={
  plain.E, plain.N, plain.W, plain.NE, plain.NE,
};
dot(node,UnFill);
for(int i=0;i<node.length;++i)label("$"+substr(nodename,i,1)+"$",node[i],nodepos[i]);
label("$CD\perp AB,\ \angle BCE=\angle ECD$",(A+C)/2,plain.S);
\end{asy}
\caption{Angle bisector with \texttt{Asymptote}}
\end{figure}
\end{document}
%
% To get bisect.pdf, process:
%
% pdflatex bisect.tex    
% asy bisect-*.asy    
% pdflatex bisect.tex

Answer 4

One tikz solution

\documentclass[11pt]{article}

\usepackage[T1]{fontenc}
\usepackage[utf8]{inputenc}

\usepackage{mathtools}
\usepackage{tikz}
\usetikzlibrary{positioning,calc,intersections}

\begin{document}
\begin{tikzpicture}

\coordinate[label=below left:$C$](C) at (-2,0);
\coordinate[label=below right:$A$](A) at (8,0);
\coordinate[label=above left:$B$] (B) at (0,7);
\coordinate[label=above right:$D$](D) at ($(A)!(C)!(B)$);

%  first name the path
\draw[name path=t1] (A) -- (B) -- (C) -- cycle;
\draw[name path=CD] (C) -- (D);

% draw circle
\path[name path=c1] (B) circle (2);
% name intersection
\path [name intersections={of = c1 and t1, by={a,b}}];
% draw line beetwen intersections
\path (a)--(b);
% draw the bissector
\path[name path=bissec] (B) -- ($(a)!0.5!(b)$) coordinate[pos=3](ff) --(ff);
\path [name intersections={of = CD and bissec, by=c}];

\draw[thick,red] (B) --(c);


\end{tikzpicture}
\end{document}

Answer 5

With MetaPost, inside a LuaLaTeX program.

The draw_mark, mark_angle and mark_right_angle macros, which make the coding much longer than it could have been, are not mandatory at all to produce the figure, but I think that this bisector figure is made clearer by marking the angles accordingly. These macros come (slightly simplified) from André Heck's wonderful tutorial in MetaPost. André Heck himself borrowed them from the MetaPost manual, and improved them at the same time.

\documentclass[12pt, border=2bp]{standalone}
\usepackage{luamplib}
  \mplibtextextlabel{enable}
\begin{document}
\begin{mplibcode}

vardef draw_mark(expr p, mark_size) =
    save t, dm;
    t = arctime .5arclength(p) of p;
    pair dm; dm = mark_size*unitvector(direction t of p rotated 90);
    draw (-.5dm -- .5dm) shifted (point t of p); 
enddef;

vardef mark_angle (expr endofa, common, endofb, mark_size) =
    save p, tn; tn := turningnumber(common -- endofa -- endofb -- cycle);
    path p; p = (unitvector(endofa-common){(endofa-common) rotated (tn*90)} 
      .. unitvector(endofb-common)) scaled mark_size shifted common;
    draw p; draw_mark(p, 5bp);
enddef ;

vardef mark_right_angle (expr endofa, common, endofb, mark_size) =
   save tn; tn := turningnumber(common -- endofa -- endofb -- cycle);
   ((1, 0) -- (1, 1) -- (0, 1))
       zscaled (mark_size*unitvector((1+tn)*endofa + (1-tn)*endofb - 2*common))
       shifted common
enddef ;

beginfig(1);
  u := cm; pair A, B, C, D, E;
  A = (8u, 0); B = (0, 7u); C = (-2u, 0);
  D = whatever[A, B] = whatever[C, C + (B-A) rotated 90];
  draw A--B--C--cycle; draw C--D;
  draw mark_right_angle(C, D, B, 2mm);
  E = C + whatever*(unitvector(D-C)+unitvector(B-C)) = whatever[A,B];
  draw C--E withcolor red;
  mark_angle (D, C, E, 1.25cm); mark_angle (B, C, E, 1.25cm);
  label.bot("$A$", A); label.lft("$B$", B); label.bot("$C$", C); label.urt("$D$", D);
endfig;

\end{mplibcode}
\end{document}

Answer 6

In addition to @g.kov's answer

// http://asymptote.ualberta.ca/
// Altitude and bisector with plain Asymptote 
// (without using the module `geometry`)
unitsize(1cm);
pair A=(4,0), B=(0,3.5), C=(-1,0);
pair Ct=reflect(A,B)*C;     // a point on the altitude
pair D=(C+Ct)/2;            // foot of the altitude
pair Et=C+dir(C--D,C--B);   // a point on the bisector
pair E=extension(A,B,C,Et); // foot of the bisector
draw(C--E,magenta);
draw(C--D,blue);
draw(A--B--C--cycle);
label("$A$",A,plain.E);
label("$B$",B,N);
label("$C$",C,W);
label("$D$",D,NE);
label("$E$",E,NE);
// with the module geometry, to mark angles
//import geometry;
//markrightangle(C,D,A);
//markangle(1,E,C,B); markangle(1.05cm,E,C,B);
//markangle(1.1cm,D,C,E); markangle(1.15cm,D,C,E);
////////////////////////////
label("$CD\perp AB$ ; and ; $\angle BCE=\angle ECD$",point(S),5S);
label("Altitude and bisector with plain Asymptote",point(N),5plain.N);
shipout(bbox(5mm,invisible,Fill(.5yellow+white))); 

With the module geometry to mark angles

Answer 7

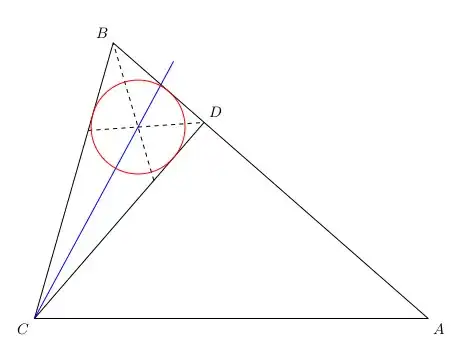
This is a ruler-and-compass construction (although, of course, TikZ calculates coordinates).

The through library is used to draw circles at a point through a point.
The calc library is used to find intersections of two circles via the intersection cs. Unfortunately, this is functionality is not documented in the manual.

You can use it either implicitly:

intersection <sol> of <first line/node> and <second line/node>

where (the optional) <sol> is either 1 or 2, i.e. the first or the second solution shall be returned and where <first line/node> is either the name of a node (of shape circle) or a line specification in the form of <c1>--<c2>. The same is true for <second line/node>.

The explicit specification is

intersection cs: first line/node=<first line/node>,
                 second line/node=<second line/node>,
                 solution=<1 or 2>

with the same parameters as above, however the lines need to be in the form of (<c1>)--(<c2>).

I've used both versions in the code below.

---

With a style like

\tikzset{
  perpendic between/.style args={#1 and #2}{
    overlay,
    insert path={
      coordinate (middle of #1 and #2) at ($(#1)!.5!(#2)$)
      coordinate (perp-#1-#2) at ($(middle of #1 and #2)!1cm!90:(#1)$)}}}

We can do

% perpendics to ABC
\path [perpendic between/.list={B and C, C and A, A and B}]
     % find intersection of two perpendics: center of circumcircle of ABC
     coordinate (circ-BCA) at (intersection cs: first line={(middle of B and C)--(perp-B-C)},
                                               second line={(middle of C and A)--(perp-C-A)});
% draw perpendics
\path[thin,blue!50] (circ-BCA) edge (middle of B and C)
                               edge (middle of C and A)
                               edge (middle of A and B);
% draw circumcircle of ABC
\node[overlay,draw=blue, at=(circ-BCA), circle through=(A)] {};

and get the circumcircle of ABC.

---

Obviously, we could package this in another style like incircle of=B-C-D or circumcircle of=A-B-C. That's just more insert paths.

Code

\documentclass[tikz]{standalone}
\usetikzlibrary{calc,through}
\tikzset{
  bisec from/.style args={#1 onto #2--#3}{
    overlay,
    insert path={
      node[at=(#1),  circle through=(#2)] (@#1-through-#2) {}
      coordinate (@#1-through-#2-to-#3) at (intersection of @#1-through-#2 and #1--#3)
      node[at=(#2), circle through=(@#1-through-#2-to-#3)] (@#2-circle)  {}
      node[at=(@#1-through-#2-to-#3), circle through=(#2)] (@#3-circle) {}
      coordinate (#1 onto #2-#3) at (intersection of @#2-circle and @#3-circle)
      coordinate (bisec-#1) at (intersection of #1--#1 onto #2-#3 and #3--#2)}}}
\begin{document}
\begin{tikzpicture}[thick]
\coordinate[label=below left:$C$] (C) at (-2,0);
\coordinate[label=below right:$A$](A) at (8,0);
\coordinate[label=above left:$B$] (B) at (0,7);
\coordinate[label=above right:$D$](D) at ($(A)!(C)!(B)$);
\draw (A) -- (B) -- (C) -- cycle;
\draw (C) -- (D);
% find point on opposite side where bisec meets
\path [bisec from/.list={C onto D--B, D onto B--C, B onto C--D}]
      % find intersection of two bisecs: center of incircle
      coordinate (incircle-BCD) at (intersection cs: first line={(B)--(bisec-B)},
                                                     second line={(C)--(bisec-C)})
      % center of incircle projected on one side
      coordinate (incircle-BCD-point) at ($(B)!(incircle-BCD)!(D)$);
% draw bisecs
\draw[thin,red!50] (C) -- (bisec-C) (D) -- (bisec-D) (B) -- (bisec-B);
% incircle
\node[draw=red, at=(incircle-BCD), circle through=(incircle-BCD-point)]{};
% circumcircle of BCD
\node[overlay,draw=red!50!black, at=($(B)!.5!(C)$), circle through=(D)]{};
\end{tikzpicture}
\end{document}

Output

Answer 8

You can use PGF's own calculation with a custom coordinate system angle bisect that uses two keys from and onto. In your case

(angle bisect cs: from = C, onto = B--D)

specifies the coordinate on the line from B to D that intersects with the angle bisector. You can then draw the line

\draw (C) -- (angle bisect cs: from = C, onto = B--D);

The order is important and onto must be given:

(angle bisect cs: onto)

defaults to

(angle bisect cs: from = B, onto = A--C)

(similar how the angle pic default to angle=A--B--C).

As with the angle pic, only the names of coordinates (or nodes) are allowed.

Code

\documentclass[tikz]{standalone}
\usetikzlibrary{calc}
\pgfqkeys{/tikz/cs/angle bisect}{
  from/.initial=B, onto/.default=A--C,
  onto/.code args={#1--#2}{%
    \pgfpointintersectionoflines{\pgfpointanchor{#1}{center}}{\pgfpointanchor{#2}{center}}
      {\pgfpointanchor{\pgfkeysvalueof{/tikz/cs/angle bisect/from}}{center}}
      {\pgfpointlineattime{.5}{%
        \pgfpointlineatdistance{+1cm}
          {\pgfpointanchor{\pgfkeysvalueof{/tikz/cs/angle bisect/from}}{center}}
          {\pgfpointanchor{#1}{center}}}{%
        \pgfpointlineatdistance{+1cm}
          {\pgfpointanchor{\pgfkeysvalueof{/tikz/cs/angle bisect/from}}{center}}
              {\pgfpointanchor{#2}{center}}}}}}
\tikzdeclarecoordinatesystem{angle bisect}{\pgfqkeys{/tikz/cs/angle bisect}{#1}}
\begin{document}
\begin{tikzpicture}[thick]
\coordinate[label=below left:$C$] (C) at (-2,0);
\coordinate[label=below right:$A$](A) at (8,0);
\coordinate[label=above left:$B$] (B) at (0,7);
\coordinate[label=above right:$D$](D) at ($(A)!(C)!(B)$);
\draw (A) -- (B) -- (C) -- cycle;
\draw (C) -- (D);
\path coordinate (bisec-C) at (angle bisect cs: from=C, onto=B--D)
      coordinate (bisec-B) at (angle bisect cs: from=B, onto=C--D)
      coordinate (bisec-D) at (angle bisect cs: from=D, onto=B--C)
      coordinate (incircle-BCD) at (intersection of B--bisec-B and C--bisec-C);
% draw bisecs
\draw[thin,red!50] (C) -- (bisec-C) (D) -- (bisec-D) (B) -- (bisec-B);
\draw[thin, dashed] (B) -- (angle bisect cs: onto); % defaults to from = B, onto = A--C
% incircle center
\fill[red,draw=black] (incircle-BCD) circle[radius=2pt];
\end{tikzpicture}
\end{document}

Output