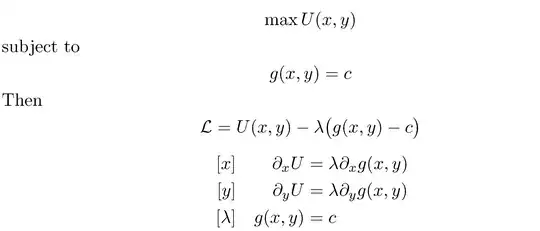4

I am doing a large number of Lagrangian multiplier problems. They are basically all the same form

$$\max U(x,y)$$
$$\text{subject to}$$
$$g(x,y) = c$$
Then
$$L = U(x,y) - \lambda (g(x,y) -c) $$

$$[x]: \partial_x U = \lambda \partial_x g(x,y)$$
$$[y]: \partial_y U = \lambda \partial_y g(x,y)$$

$$[\lambda]: g(x,y) = c$$

I obviously can write it up as I have done here, but it is kind of tedious to type. It is also ugly when I copy and paste and then rewrite new formulas in. It would be easier it there was code way to do this. Like an environment like enumerate where I could just say \item and then list the first order conditions. And something that would automatically list all my constraints as part of the FOCs. It would also be nice if I didn't have to write out the Lagrangian, but it could simply take the equations I wrote in the initial set up and output the Lagrangian for me.

Is there a package that does this? If not, any thoughts on how I could code the above?

If its too much effort, I bother with it. But I thought I would ask if there is a simple solution.

Mico
  • 506,678
Stan Shunpike
  • 467

1 Answers1

9

I don't think there's a ready-made package for Lagrangean equations. Applying a bit more formatting -- and not using $$ in a LaTeX document -- may be desirable. I suggest using a gather* environment, with a nested alignedat environment.

enter image description here

\documentclass{article}
\usepackage{mathtools}
\begin{document}

\begin{gather}
\max U(x,y)\
\shortintertext{subject to}
g(x,y) = c\
\shortintertext{Then}
\mathcal{L} = U(x,y) - \lambda \bigl(g(x,y) -c\bigr) \[1ex]
\begin{alignedat}{2}
&[x] &       \partial_x U &= \lambda \partial_x g(x,y)\
&[y] &       \partial_y U &= \lambda \partial_y g(x,y)\
&[\lambda] & \quad g(x,y) &= c
\end{alignedat}
\end{gather}


\end{document}
Mico
  • 506,678