2

I am attempting to plot a region in TikZ using data exported from a Mathematica RegionPlot. But the TikZ \filldraw command is giving me a strange-looking output. The problem with the generated TikZ picture is that it doesn't generate a smooth region and there are black lines obscuring the image for some reason.

The TikZ result

It's possible that something went wrong in the export process from Mathematica. So I'll include my Mathematica code used to generate the plot and export it to a .txt file.

LaTeX

\documentclass{standalone}
\usepackage{tikz}

\usetikzlibrary{arrows}
\usetikzlibrary{calc,through,backgrounds}
\usepackage{pgfplots}
\usepackage{amsfonts}
\usepgfplotslibrary{fillbetween}
\pgfplotsset{compat=1.8}

\begin{document}

\begin{tikzpicture}[scale=2]

\filldraw[color=black, fill=blue!50, opacity = 1] plot coordinates {
(-0.473684160664820, -0.15789472022160686) (-0.3684210138504157, -0.15789472022160686) (-0.2631578670360113,
-0.15789472022160686) (-0.15789472022160686, -0.15789472022160686) (-0.5789473074792245, -0.052631573407202425)
(-0.4736841606648201, -0.052631573407202425) (-0.3684210138504157, -0.052631573407202425) (-0.2631578670360113,
-0.052631573407202425) (-0.15789472022160686, -0.052631573407202425) (-0.052631573407202425, -0.052631573407202425)
(-0.5789473074792245, 0.05263157340720201) (-0.4736841606648201, 0.05263157340720201) (-0.3684210138504157,
0.05263157340720201) (-0.2631578670360113, 0.05263157340720201) (-0.15789472022160686, 0.05263157340720201)
(-0.052631573407202425, 0.05263157340720201) (-0.4736841606648201, 0.15789472022160644) (-0.3684210138504157,
0.15789472022160644) (-0.2631578670360113, 0.15789472022160644) (-0.15789472022160686, 0.15789472022160644)
(-0.4210525872576179, -0.2105262936288091) (-0.5263157340720224, -0.10526314681440464) (-0.3157894404432135,
-0.2105262936288091) (-0.2105262936288091, -0.2105262936288091) (-0.10526314681440464, -0.10526314681440464)
(-0.5789473074792245, -0.10526314681440464) (-0.6315788808864267, 0) (-0.5263157340720224,
0.10526314681440423) (-0.10526314681440464, 0.10526314681440423) (-0.052631573407202425, 0.10526314681440423)
(-0.4210525872576179, 0.21052629362880865) (-0.3157894404432135, 0.21052629362880865) (-0.2105262936288091,
0.21052629362880865) (-0.15789472022160686, 0.21052629362880865) (-0.4736841606648201, -0.2105262936288091)
(-0.5263157340720224, -0.15789472022160686) (-0.3684210138504157, -0.2105262936288091) (-0.2631578670360113,
-0.2105262936288091) (-0.15789472022160686, -0.2105262936288091) (-0.10526314681440464, -0.15789472022160686)
(-0.6315788808864267, -0.052631573407202425) (-0.052631573407202425, -0.10526314681440464) (-0.6315788808864267,
0.05263157340720201) (-0.5789473074792245, 0.10526314681440423) (-0.5263157340720224, 0.15789472022160644)
(-0.10526314681440464, 0.15789472022160644) (-0.4736841606648201, 0.21052629362880865) (-0.3684210138504157,
0.21052629362880865) (-0.2631578670360113, 0.21052629362880865) (-0.49999994736842124, -0.18421050692520796)
(-0.6052630941828256, -0.07894736011080353) (-0.07894736011080353, 0.13157893351800534) (-0.5526315207756234,
-0.13157893351800576) (-0.13157893351800576, -0.18421050692520796) (-0.07894736011080353, -0.13157893351800576)
(-0.026315786703601317, -0.07894736011080353) (-0.6052630941828256, 0.07894736011080311) (-0.026315786703601317,
0.07894736011080311) (-0.5526315207756234, 0.13157893351800534) (-0.49999994736842124, 0.18421050692520755)
(-0.13157893351800576, 0.18421050692520755) (-0.39473680055401683, -0.2368420803324102) (-0.34210522714681457,
-0.2368420803324102) (-0.2894736537396124, -0.2368420803324102) (-0.2368420803324102, -0.2368420803324102)
(-0.18421050692520796, -0.2368420803324102) (-0.10526314681440464, 0)
(-0.052631573407202425, 0) (-0.026315786703601317, -0.026315786703601317)
(-0.026315786703601317, 0.0263157867036009) (-0.34210522714681457, 0.23684208033240975) (-0.2368420803324102,
0.23684208033240975) (-0.18421050692520796, 0.23684208033240975) (-0.026315786703601317, -0.052631573407202425)
(-0.026315786703601317, 0.05263157340720201) (-0.39473680055401683, 0.23684208033240975) (-0.3684210138504157,
0.23684208033240975) (-0.2894736537396124, 0.23684208033240975) (-0.2631578670360113, 0.23684208033240975)
(-0.4736841606648201, -0.22080589780990328) (-0.3684210138504157, -0.25421461139845936) (-0.2631578670360113,
-0.2582750550499915) (-0.15789472022160686, -0.22985194948926613) (-0.060444072584834, -0.15789472022160686)
(-0.5789473074792245, -0.1484374843750002) (-0.052631573407202425, -0.1484374843750002) (-0.060444072584834,
0.15789472022160644) (-0.05694900716326198, 0.15357728646554686) (-0.3794201903241865, 0.25215869056224005)
(-0.26762949485478726, 0.2586862392172349) (-0.18153780983812345, 0.23951477741949423) (-0.44387330853964696,
-0.23334701491083817) (-0.1120476855739268, -0.20374175486928692) (-0.6138979616949447, -0.10526314681440464)
(-0.6464329089281079, -0.014854028041681303) (-0.6464329089281079, 0.014854028041680886) (-0.017475327107860317,
-0.08778781970654453) (-0.00020559208362209183, -0.00020559208362209183) (-0.00020559208362209183,
0.0002055920836216755) (-0.6206825004544669, 0.0943667663824444) (-0.017475327107860317, 0.08778781970654412)
(-0.514596985305575, 0.19880754486236127) (-0.052631573407202425, 0.14843748437499982) (-0.0252878262854919,
0.10526314681440423) (-0.1120476855739268, 0.20374175486928647) (-0.44387330853964696, 0.23334701491083773)
(-0.15789472022160686, 0.22985194948926568) (-0.1221216976713991, 0.21052629362880865) (-0.49426906803746123,
-0.2105262936288091) (-0.569181683507185, -0.15789472022160686) (-0.5263157340720224, -0.191200637768352)
(-0.1221216976713991, -0.2105262936288091) (-0.10526314681440464, -0.19911593298779456) (-0.6390829919386254,
-0.052631573407202425) (-0.6315788808864267, -0.07277959760214701) (-0.0252878262854919, -0.10526314681440464)
(-0.006167762508656718, -0.052631573407202425) (-0.6390829919386254, 0.05263157340720201) (-0.6315788808864267,
0.0727795976021466) (-0.006167762508656718, 0.05263157340720201) (-0.5789473074792245, 0.14843748437499982)
(-0.6138979616949447, 0.10526314681440423) (-0.569181683507185, 0.15789472022160644) (-0.5263157340720224,
0.1912006377683516) (-0.10526314681440464, 0.19911593298779412) (-0.4736841606648201, 0.22080589780990284)
(-0.49426906803746123, 0.21052629362880865) (-0.514596985305575, -0.1988075448623617) (-0.6206825004544669,
-0.09436676638244482) (-0.5742186895559211, -0.15316610229830355) (-0.05694900716326198, -0.1535772864655473)
(-0.008120887303064612, -0.060752460710266826) (-0.008120887303064612, 0.06075246071026641) (-0.5742186895559211,
0.1531661022983031) (-0.4210525872576179, 0.2411595140884693) (-0.3157894404432135, 0.2599197917189662)
(-0.2105262936288091, 0.248766421182479) (-0.4210525872576179, -0.24115951408846975) (-0.4553864652224725,
-0.22882398907115672) (-0.3794201903241865, -0.2521586905622405) (-0.40398844431700154, -0.24609372409539496)
(-0.3157894404432135, -0.2599197917189666) (-0.36071131071459506, -0.25544816390019065) (-0.3192845058647855,
-0.2596628016144392) (-0.26762949485478726, -0.2586862392172353) (-0.31260276314707436, -0.2599711897398721)
(-0.2105262936288091, -0.24876642118247944) (-0.2576068807782204, -0.2576068807782204) (-0.22224504239525647,
-0.2514391182695639) (-0.18153780983812345, -0.23951477741949467) (-0.19006988130843167, -0.24270145471563387)
(-0.6467926950744461, 0) (-0.6419098830884263, -0.042300571205202774) (-0.6419098830884263,
0.04230057120520236) (-0.0004111841672439755, 0) (-0.0051398020905473,
-0.047491771316655336) (-0.0051398020905473, 0.04749177131665492) (-0.4553864652224725, 0.22882398907115628)
(-0.36071131071459506, 0.2554481639001902) (-0.3192845058647855, 0.2596628016144388) (-0.2576068807782204,
0.25760688077821997) (-0.22224504239525647, 0.25143911826956344) (-0.19006988130843167, 0.24270145471563342)
(-0.40398844431700154, 0.2460937240953945) (-0.3684210138504157, 0.2542146113984589) (-0.31260276314707436,
0.25997118973987166) (-0.2631578670360113, 0.25827505504999104) (-0.48046869942434234, -0.21731083238833127)
(-0.14494241895342821, -0.22347859489698776) (-0.08259661959509196, -0.1805612474409195) (-0.5993009237577911,
-0.12561676309297112) (-0.03492495520526769, -0.12296976501633936) (-0.08259661959509196, 0.18056124744091911)
(-0.03492495520526769, 0.12296976501633894) (-0.5458469820161012, -0.1774259681656858) (-0.6371298671442176,
-0.058182559664993284) (-0.6371298671442176, 0.05818255966499287) (-0.5458469820161012, 0.17742596816568537)
(-0.5993009237577911, 0.1256167630929707) (-0.48046869942434234, 0.21731083238833082)};
\end{tikzpicture}
\end{document}

Mathematica Code

\[Mu] = {1, 2, 3, 4, 5, 6};
plot = RegionPlot[
    Product[Abs[1 + \[Mu] (x + I y)]^1, {\[Mu], 1, 6}] < 1,
   {x, -1, 1}, {y, -1, 1},
  PlotRange -> Automatic,
  GridLines -> Automatic,
  AspectRatio -> Automatic]

Export[NotebookDirectory[] <> "dice.txt", plot]

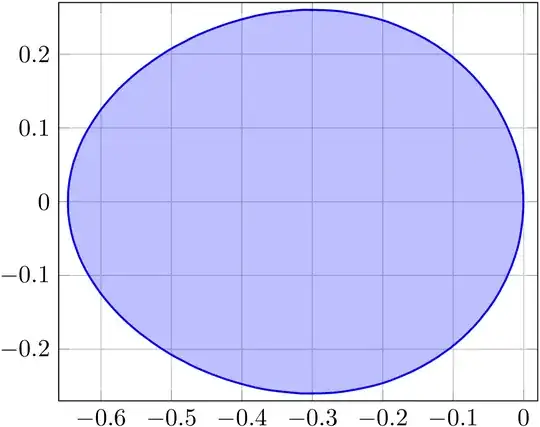
Here is the Mathematica plot I am wanting to reproduce:

the desired image

Here is a link to dice.txt in case you don't have mathematica.

I also tried a scatter plot of these points in MATLAB and got this:

MATLAB output

So, apparently I'm not dealing exclusively with coordinates on the border.

Svend Tveskæg
  • 31,033
Guilty Spark
  • 21
  • If you use \fill instead of \filldraw a blue region with some white areas inside is shown. Is this what you want? – Ignasi May 26 '15 at 16:10
  • Could you edit your question to include dice.txt? (I can't run the Mathematica code for lack of Mathematica) – Jake May 26 '15 at 16:28
  • Could you upload the mathematica generated image so that we know the intended appearance, You can use the image upload button but delete the ! from the generated markup, then the image will be uploaded as a link, one of us can then add the ! back to make the image be inline. – David Carlisle May 26 '15 at 16:34
  • @DavidCarlisle Okay, apparently I am able to add inline images. I hope that helps clarify my question. – Guilty Spark May 26 '15 at 18:41
  • @Jake I added a link to dice.txt. It has a bunch of other stuff in addition to the coordinates that I had to delete first. Also, I had to replace brackets with parentheses as well as delete some commas. – Guilty Spark May 26 '15 at 18:48
  • @Jake I should also mentioned that dice.txt has some really small numbers (-2.081*^-16) that I replaced with zeros. The exponents were causing Tex errors for some reason. – Guilty Spark May 26 '15 at 18:53
  • I think your points are scrambled instead of separated into different regions. And they are all connected consecutively leading to this mayhem. They need to be ordered to match the mathematica output – percusse May 26 '15 at 19:03
  • @percusse You are probably right. I'm sure there is a better way to export the image than Export[NotebookDirectory[] <> "dice.txt", plot], but haven't found anything that works specifically with RegionPlot. – Guilty Spark May 26 '15 at 19:06
  • If you can export the region one by one for each mu. Then they will be exported in order I think. So you can use multiple paths and fill inside them. I don't have mathematica so I can't judge. – percusse May 26 '15 at 19:08
  • Isn't this basically a polar plot with changing x factor? For example: \tikz\path[draw=blue!80, fill=blue!20, delta angle=180, y radius=.26] (-90:.26) arc[start angle=-90, x radius=.3] arc[start angle=90, x radius=.34] -- cycle; Related: How can I draw an egg using TikZ? – Qrrbrbirlbel May 26 '15 at 19:50

1 Answers1

7

First the serious part. The coordinates are quite messed up. For the following example I have:

  • sorted the points,
  • removed inside points with a point of the same x coordinate,
  • removing the remaining inside points manually,
  • added closed hobby for a smoother curve.

Full example file:

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{hobby}
\usepackage{pgfplots}
\pgfplotsset{compat=1.12}

\usepackage[active, tightpage]{preview}
\PreviewEnvironment[{[]}]{tikzpicture}

\begin{document}
\begin{tikzpicture}
\begin{axis}[
  xmin=-.66,
  xmax=.02,
  ymin=-.27,
  ymax=.27,
  grid,
]
  \addplot[
    closed hobby,
    thick,
    blue,
    fill=blue,
    fill opacity=.25,
  ] coordinates {
(-0.6464329089281079, -0.014854028041681303)
(-0.6419098830884263, -0.042300571205202774)
(-0.6390829919386254, -0.052631573407202425)
(-0.6371298671442176, -0.058182559664993284)
(-0.6315788808864267, -0.07277959760214701)
(-0.6206825004544669, -0.09436676638244482)
(-0.6138979616949447, -0.10526314681440464)
%(-0.6052630941828256, -0.07894736011080353)
(-0.5993009237577911, -0.12561676309297112)
(-0.5789473074792245, -0.1484374843750002)
(-0.5742186895559211, -0.15316610229830355)
(-0.569181683507185, -0.15789472022160686)
%(-0.5526315207756234, -0.13157893351800576)
(-0.5458469820161012, -0.1774259681656858)
(-0.5263157340720224, -0.191200637768352)
(-0.514596985305575, -0.1988075448623617)
%(-0.49999994736842124, -0.18421050692520796)
(-0.49426906803746123, -0.2105262936288091)
(-0.48046869942434234, -0.21731083238833127)
(-0.4736841606648201, -0.22080589780990328)
%(-0.473684160664820, -0.15789472022160686)
(-0.4553864652224725, -0.22882398907115672)
(-0.44387330853964696, -0.23334701491083817)
(-0.4210525872576179, -0.24115951408846975)
(-0.40398844431700154, -0.24609372409539496)
%(-0.39473680055401683, -0.2368420803324102)
(-0.3794201903241865, -0.2521586905622405)
(-0.3684210138504157, -0.25421461139845936)
(-0.36071131071459506, -0.25544816390019065)
%(-0.34210522714681457, -0.2368420803324102)
(-0.3192845058647855, -0.2596628016144392)
(-0.3157894404432135, -0.2599197917189666)
(-0.31260276314707436, -0.2599711897398721)
%(-0.2894736537396124, -0.2368420803324102)
(-0.26762949485478726, -0.2586862392172353)
(-0.2631578670360113, -0.2582750550499915)
(-0.2576068807782204, -0.2576068807782204)
%(-0.2368420803324102, -0.2368420803324102)
(-0.22224504239525647, -0.2514391182695639)
(-0.2105262936288091, -0.24876642118247944)
(-0.19006988130843167, -0.24270145471563387)
%(-0.18421050692520796, -0.2368420803324102)
(-0.18153780983812345, -0.23951477741949467)
(-0.15789472022160686, -0.22985194948926613)
(-0.14494241895342821, -0.22347859489698776)
%(-0.13157893351800576, -0.18421050692520796)
(-0.1221216976713991, -0.2105262936288091)
(-0.1120476855739268, -0.20374175486928692)
(-0.10526314681440464, -0.19911593298779456)
(-0.08259661959509196, -0.1805612474409195)
%(-0.07894736011080353, -0.13157893351800576)
(-0.060444072584834, -0.15789472022160686)
(-0.05694900716326198, -0.1535772864655473)
(-0.052631573407202425, -0.1484374843750002)
(-0.03492495520526769, -0.12296976501633936)
%(-0.026315786703601317, -0.07894736011080353)
(-0.0252878262854919, -0.10526314681440464)
(-0.017475327107860317, -0.08778781970654453)
(-0.008120887303064612, -0.060752460710266826)
(-0.006167762508656718, -0.052631573407202425)
(-0.0051398020905473, -0.047491771316655336)
%(-0.00020559208362209183, -0.00020559208362209183)
%(-0.00020559208362209183, 0.0002055920836216755)
(-0.0004111841672439755, 0)
(-0.0051398020905473, 0.04749177131665492)
(-0.006167762508656718, 0.05263157340720201)
(-0.008120887303064612, 0.06075246071026641)
(-0.017475327107860317, 0.08778781970654412)
(-0.0252878262854919, 0.10526314681440423)
%(-0.026315786703601317, 0.07894736011080311)
(-0.03492495520526769, 0.12296976501633894)
(-0.052631573407202425, 0.14843748437499982)
(-0.05694900716326198, 0.15357728646554686)
(-0.060444072584834, 0.15789472022160644)
%(-0.07894736011080353, 0.13157893351800534)
(-0.08259661959509196, 0.18056124744091911)
(-0.10526314681440464, 0.19911593298779412)
(-0.1120476855739268, 0.20374175486928647)
(-0.1221216976713991, 0.21052629362880865)
%(-0.13157893351800576, 0.18421050692520755)
(-0.15789472022160686, 0.22985194948926568)
(-0.18153780983812345, 0.23951477741949423)
%(-0.18421050692520796, 0.23684208033240975)
(-0.19006988130843167, 0.24270145471563342)
(-0.2105262936288091, 0.248766421182479)
(-0.22224504239525647, 0.25143911826956344)
%(-0.2368420803324102, 0.23684208033240975)
(-0.2576068807782204, 0.25760688077821997)
(-0.2631578670360113, 0.25827505504999104)
(-0.26762949485478726, 0.2586862392172349)
%(-0.2894736537396124, 0.23684208033240975)
(-0.31260276314707436, 0.25997118973987166)
(-0.3157894404432135, 0.2599197917189662)
(-0.3192845058647855, 0.2596628016144388)
%(-0.34210522714681457, 0.23684208033240975)
(-0.36071131071459506, 0.2554481639001902)
(-0.3684210138504157, 0.2542146113984589)
(-0.3794201903241865, 0.25215869056224005)
%(-0.39473680055401683, 0.23684208033240975)
(-0.40398844431700154, 0.2460937240953945)
(-0.4210525872576179, 0.2411595140884693)
(-0.44387330853964696, 0.23334701491083773)
(-0.4553864652224725, 0.22882398907115628)
(-0.4736841606648201, 0.22080589780990284)
(-0.48046869942434234, 0.21731083238833082)
(-0.49426906803746123, 0.21052629362880865)
%(-0.49999994736842124, 0.18421050692520755)
(-0.514596985305575, 0.19880754486236127)
(-0.5263157340720224, 0.1912006377683516)
(-0.5458469820161012, 0.17742596816568537)
%(-0.5526315207756234, 0.13157893351800534)
(-0.569181683507185, 0.15789472022160644)
(-0.5742186895559211, 0.1531661022983031)
(-0.5789473074792245, 0.14843748437499982)
(-0.5993009237577911, 0.1256167630929707)
%(-0.6052630941828256, 0.07894736011080311)
(-0.6138979616949447, 0.10526314681440423)
(-0.6206825004544669, 0.0943667663824444)
(-0.6315788808864267, 0.0727795976021466)
(-0.6371298671442176, 0.05818255966499287)
(-0.6390829919386254, 0.05263157340720201)
(-0.6419098830884263, 0.04230057120520236)
(-0.6464329089281079, 0.014854028041680886)
(-0.6467926950744461, 0)
  };
\end{axis}
\end{tikzpicture}
\end{document}

Serious result

Ah, now the opportunity for creating art!

First example applies smoothing and plays with the tension. Also the scale factor is reduced along with the raising of the tension to keep an approximately equal shape of the image:

\documentclass{article}
\usepackage{tikz}
\usepackage[active, tightpage]{preview}
\PreviewEnvironment[{[]}]{tikzpicture}

\begin{document}
\newcommand*{\img}{%
  \begin{tikzpicture}
    \def\w{1}
    \def\h{.52}
    \useasboundingbox (-1.3*\w, -\h) rectangle (1.05*\w, \h);
    \tikzset{scale=\scale}
    \filldraw[line width=.03pt, color=black, fill=blue!50]
      plot[smooth, tension=\tension] coordinates {
        % coordinates from the question
    };
  \end{tikzpicture}%
}
\foreach \i in {0, .1, ..., 5.9} {
  \pgfmathsetmacro\tension{exp(\i)-1}%
  \pgfmathsetmacro\scale{2/(\tension/4.1 + 1)}%
  \img
}
\end{document}

First art image

Second art example without changing the scale factor:

\documentclass{article}
\usepackage{tikz}
\usepackage[active, tightpage]{preview}
\PreviewEnvironment[{[]}]{tikzpicture}

\begin{document}
\newcommand*{\img}[1]{%
  \begin{tikzpicture}[scale=1]
    \def\w{10}
    \def\h{10}
    \useasboundingbox (-\w, -\h) rectangle (\w, \h);
    \filldraw[line width=.03pt, color=black, fill=blue!50, overlay]
      plot[smooth, tension=#1] coordinates {
        % coordinates from the question
    };
  \end{tikzpicture}%
}
\foreach \i in {0, .1, ..., 5.9} {
  \pgfmathsetmacro\tension{exp(\i)-1}%
  \img\tension
}
\end{document}

Second art example

The third example is an image with sorted coordinates:

\documentclass{article}
\usepackage{tikz}
\usepackage[active, tightpage]{preview}
\PreviewEnvironment[{[]}]{tikzpicture}

\begin{document}
\begin{tikzpicture}
  \draw[line width=.1pt, scale=4]
    plot coordinates {
(-0.00020559208362209183, -0.00020559208362209183)
(-0.0051398020905473, -0.047491771316655336)
(-0.006167762508656718, -0.052631573407202425)
(-0.008120887303064612, -0.060752460710266826)
(-0.017475327107860317, -0.08778781970654453)
(-0.0252878262854919, -0.10526314681440464)
(-0.026315786703601317, -0.026315786703601317)
(-0.026315786703601317, -0.052631573407202425)
(-0.026315786703601317, -0.07894736011080353)
(-0.03492495520526769, -0.12296976501633936)
(-0.052631573407202425, -0.052631573407202425)
(-0.052631573407202425, -0.10526314681440464)
(-0.052631573407202425, -0.1484374843750002)
(-0.05694900716326198, -0.1535772864655473)
(-0.060444072584834000, -0.15789472022160686)
(-0.078947360110803530, -0.13157893351800576)
(-0.08259661959509196, -0.1805612474409195)
(-0.10526314681440464, -0.19911593298779456)
(-0.105263146814404640, -0.10526314681440464)
(-0.105263146814404640, -0.15789472022160686)
(-0.112047685573926800, -0.20374175486928692)
(-0.1221216976713991, -0.2105262936288091)
(-0.131578933518005760, -0.18421050692520796)
(-0.14494241895342821, -0.22347859489698776)
(-0.157894720221606860, -0.052631573407202425)
(-0.157894720221606860, -0.15789472022160686)
(-0.157894720221606860, -0.2105262936288091)
(-0.157894720221606860, -0.22985194948926613)
(-0.18153780983812345, -0.23951477741949467)
(-0.184210506925207960, -0.2368420803324102)
(-0.19006988130843167, -0.24270145471563387)
(-0.2105262936288091, -0.24876642118247944)
(-0.210526293628809100, -0.2105262936288091)
(-0.22224504239525647, -0.2514391182695639)
(-0.236842080332410200, -0.2368420803324102)
(-0.2576068807782204, -0.2576068807782204)
(-0.263157867036011300, -0.052631573407202425)
(-0.263157867036011300, -0.15789472022160686)
(-0.263157867036011300, -0.2105262936288091)
(-0.263157867036011300, -0.2582750550499915)
(-0.26762949485478726, -0.2586862392172353)
(-0.289473653739612400, -0.2368420803324102)
(-0.31260276314707436, -0.2599711897398721)
(-0.3157894404432135, -0.2599197917189666)
(-0.315789440443213500, -0.2105262936288091)
(-0.3192845058647855, -0.2596628016144392)
(-0.342105227146814570, -0.2368420803324102)
(-0.36071131071459506, -0.25544816390019065)
(-0.368421013850415700, -0.052631573407202425)
(-0.368421013850415700, -0.15789472022160686)
(-0.368421013850415700, -0.2105262936288091)
(-0.368421013850415700, -0.25421461139845936)
(-0.3794201903241865, -0.2521586905622405)
(-0.394736800554016830, -0.2368420803324102)
(-0.40398844431700154, -0.24609372409539496)
(-0.4210525872576179, -0.24115951408846975)
(-0.421052587257617900, -0.2105262936288091)
(-0.443873308539646960, -0.23334701491083817)
(-0.4553864652224725, -0.22882398907115672)
(-0.473684160664820000, -0.15789472022160686)
(-0.473684160664820100, -0.052631573407202425)
(-0.473684160664820100, -0.2105262936288091)
(-0.473684160664820100, -0.22080589780990328)
(-0.48046869942434234, -0.21731083238833127)
(-0.49426906803746123, -0.2105262936288091)
(-0.499999947368421240, -0.18421050692520796)
(-0.514596985305575, -0.1988075448623617)
(-0.5263157340720224, -0.191200637768352)
(-0.526315734072022400, -0.10526314681440464)
(-0.526315734072022400, -0.15789472022160686)
(-0.5458469820161012, -0.1774259681656858)
(-0.552631520775623400, -0.13157893351800576)
(-0.569181683507185, -0.15789472022160686)
(-0.5742186895559211, -0.15316610229830355)
(-0.578947307479224500, -0.052631573407202425)
(-0.578947307479224500, -0.10526314681440464)
(-0.578947307479224500, -0.1484374843750002)
(-0.5993009237577911, -0.12561676309297112)
(-0.605263094182825600, -0.07894736011080353)
(-0.613897961694944700, -0.10526314681440464)
(-0.6206825004544669, -0.09436676638244482)
(-0.6315788808864267, -0.07277959760214701)
(-0.631578880886426700, -0.052631573407202425)
(-0.6371298671442176, -0.058182559664993284)
(-0.6390829919386254, -0.052631573407202425)
(-0.6419098830884263, -0.042300571205202774)
(-0.646432908928107900, -0.014854028041681303)
(-0.6467926950744461, 0)
(-0.646432908928107900, 0.014854028041680886)
(-0.6419098830884263, 0.04230057120520236)
(-0.6390829919386254, 0.05263157340720201)
(-0.6371298671442176, 0.05818255966499287)
(-0.631578880886426700, 0.05263157340720201)
(-0.631578880886426700, 0)
(-0.6315788808864267, 0.0727795976021466)
(-0.6206825004544669, 0.0943667663824444)
(-0.6138979616949447, 0.10526314681440423)
(-0.605263094182825600, 0.07894736011080311)
(-0.5993009237577911, 0.1256167630929707)
(-0.578947307479224500, 0.10526314681440423)
(-0.578947307479224500, 0.05263157340720201)
(-0.5789473074792245, 0.14843748437499982)
(-0.5742186895559211, 0.1531661022983031)
(-0.569181683507185, 0.15789472022160644)
(-0.552631520775623400, 0.13157893351800534)
(-0.5458469820161012, 0.17742596816568537)
(-0.526315734072022400, 0.15789472022160644)
(-0.526315734072022400, 0.10526314681440423)
(-0.5263157340720224, 0.1912006377683516)
(-0.514596985305575, 0.19880754486236127)
(-0.499999947368421240, 0.18421050692520755)
(-0.49426906803746123, 0.21052629362880865)
(-0.48046869942434234, 0.21731083238833082)
(-0.473684160664820100, 0.21052629362880865)
(-0.473684160664820100, 0.15789472022160644)
(-0.473684160664820100, 0.05263157340720201)
(-0.4736841606648201, 0.22080589780990284)
(-0.4553864652224725, 0.22882398907115628)
(-0.44387330853964696, 0.23334701491083773)
(-0.421052587257617900, 0.21052629362880865)
(-0.4210525872576179, 0.2411595140884693)
(-0.40398844431700154, 0.2460937240953945)
(-0.394736800554016830, 0.23684208033240975)
(-0.379420190324186500, 0.25215869056224005)
(-0.368421013850415700, 0.23684208033240975)
(-0.368421013850415700, 0.21052629362880865)
(-0.368421013850415700, 0.15789472022160644)
(-0.368421013850415700, 0.05263157340720201)
(-0.3684210138504157, 0.2542146113984589)
(-0.36071131071459506, 0.2554481639001902)
(-0.342105227146814570, 0.23684208033240975)
(-0.3192845058647855, 0.2596628016144388)
(-0.315789440443213500, 0.21052629362880865)
(-0.3157894404432135, 0.2599197917189662)
(-0.31260276314707436, 0.25997118973987166)
(-0.289473653739612400, 0.23684208033240975)
(-0.267629494854787260, 0.2586862392172349)
(-0.263157867036011300, 0.23684208033240975)
(-0.263157867036011300, 0.21052629362880865)
(-0.263157867036011300, 0.15789472022160644)
(-0.263157867036011300, 0.05263157340720201)
(-0.2631578670360113, 0.25827505504999104)
(-0.2576068807782204, 0.25760688077821997)
(-0.236842080332410200, 0.23684208033240975)
(-0.22224504239525647, 0.25143911826956344)
(-0.210526293628809100, 0.21052629362880865)
(-0.2105262936288091, 0.248766421182479)
(-0.19006988130843167, 0.24270145471563342)
(-0.184210506925207960, 0.23684208033240975)
(-0.181537809838123450, 0.23951477741949423)
(-0.157894720221606860, 0.21052629362880865)
(-0.157894720221606860, 0.15789472022160644)
(-0.157894720221606860, 0.05263157340720201)
(-0.15789472022160686, 0.22985194948926568)
(-0.131578933518005760, 0.18421050692520755)
(-0.1221216976713991, 0.21052629362880865)
(-0.1120476855739268, 0.20374175486928647)
(-0.105263146814404640, 0.15789472022160644)
(-0.105263146814404640, 0.10526314681440423)
(-0.105263146814404640, 0)
(-0.10526314681440464, 0.19911593298779412)
(-0.08259661959509196, 0.18056124744091911)
(-0.078947360110803530, 0.13157893351800534)
(-0.060444072584834000, 0.15789472022160644)
(-0.056949007163261980, 0.15357728646554686)
(-0.052631573407202425, 0.14843748437499982)
(-0.052631573407202425, 0.10526314681440423)
(-0.052631573407202425, 0.05263157340720201)
(-0.052631573407202425, 0)
(-0.03492495520526769, 0.12296976501633894)
(-0.026315786703601317, 0.07894736011080311)
(-0.026315786703601317, 0.05263157340720201)
(-0.026315786703601317, 0.0263157867036009)
(-0.0252878262854919, 0.10526314681440423)
(-0.017475327107860317, 0.08778781970654412)
(-0.008120887303064612, 0.06075246071026641)
(-0.006167762508656718, 0.05263157340720201)
(-0.0051398020905473, 0.04749177131665492)
(-0.0004111841672439755, 0)
(-0.00020559208362209183, 0.0002055920836216755)
  };
\end{tikzpicture}
\end{document}

Result with sorted coordinates

Heiko Oberdiek
  • 271,626