tikz projection parallel to given line

Question

Consider the MWE below.

I've marked the projection of A onto the Y-axis parallel to the X-axis. Now my question is whether there is an easy method of doing the projection of A onto the Y-axis, but parallel to the given line?

Until now I've been using intersections between temp curves and the Y-axis. I'd like to know if there is something easier already build in.

\documentclass[a4paper]{memoir}
\usepackage{tikz}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
  \draw[<->] (0,3) -- (0,0) -- (3,0);
   \draw (0,0) -- (3,1);
   \fill (2,2) coordinate (A) circle (2pt) node[right] {A};
   \draw[dashed] (A) -- ($(A -| 0,0)$);
\end{tikzpicture}
\end{document}

tkz-euclide package and this answer may help you: http://tex.stackexchange.com/a/114737/31034 — , Nov 06 '15 at 10:47
@ferahfeza isn't that just generating parallel lines? Because that is easy enough — daleif, Nov 06 '15 at 10:52
You don't need calc : you may use (A -| 0,0) instead of ($(A -| 0,0)$)... — Paul Gaborit, Nov 06 '15 at 12:50
@PaulGaborit, I know, that is not the problem here, that line just shows the projection parallel with the x axis. — daleif, Nov 06 '15 at 13:09

Matthew Leingang · Answer 1 · 2017-05-25T15:01:43.690

There are a couple of lightly documented TikZ features that are useful here:

When using coordinate calculations to project one coordinate onto the line between two others, an angle can be added to rotate the new coordinate around the coordinate which is projected. That is, ($(A)!(B)!(C)$) projects (C) onto the line between (A) and (B), and ($(A)!(B)!:<n>(C)$) rotates that coordinate about (C) by an angle <n>.
There is an intersection coordinate system (apart from the intersections library which places a coordinate at the intersection of two lines, each specified by two coordinates. The syntax is (intersection of A--B and C--D) (no parentheses around the coordinates). This feature is better for this use case than creating paths between the pairs of points and using name intersections, because the latter will only work if the line segments intersect and not the (infinitely long) lines.

With those in mind, the idea is to project from the initial coordinate to the first line, then rotate the resulting coordinate by 90 degrees. The line between the initial coordinated and the projected-then-rotated coordinate is parallel to the first line. We can then intersect it with the second line. Here is how to do that in your MWE:

\documentclass{standalone}
\usepackage{tikz}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
  \useasboundingbox (-0.1,-0.1) rectangle (3.1,3.1); 
  \draw[<->] (0,3) -- (0,0) -- (3,0);
   \draw (0,0) -- (3,1);
   \fill (2,2) coordinate (A) circle (2pt) node[right] {A};
   \coordinate (B) at ($(0,0)!(A)!90:(3,1)$);
   \draw[gray] (A) -- (intersection of A--B and 0,0--0,1);
\end{tikzpicture}
\end{document}

The next question is: what is the “TikZ way” to encapsulate this process? The operation of projecting one coordinate onto a line, parallel to a line, involves five inputs: the coordinate to be projected, plus two for each line. A simple macro would require five parameters; possibly a sixth if one is the name of the coordinate to be created. Plus macros are not really compatible with TikZ's focus on paths as the main object.

It is a kind of calculation, but as far as I can tell coordinate calculations are not intended to be extended by the user. Plus, I find the syntax of coordinate calculations a little close to xy-pic-level density. No offense to XY-Pic, but I think the syntax was a key factor in how TikZ became the category killer.

TikZ does provide a mechanism for defining coordinate systems, though. Common coordinate system is polar, in which you can describe points by radius and angle. But pgfplots uses many coordinate systems for positioning coordinates on the graph window, the axes, the tick labels, etc. A coordinate system can do whatever it wants with its input; it just needs to return a coordinate.

So I sought to create a coordinate system parallel to the following interface:

(parallel cs:from=P, to=A--B, on=C--D)

should specify the coordinate (P) projected onto the line defined by (A) and (B), parallel to the line defined by (C) and (D).

According to the manual, coordinate systems can be implemented with \tikzdeclarecoordinatesystem{<name>}{<code>} The <code> takes as parameter text the text between (<name> cs: and ). Typically that text is run through \setkeys, \pgfkeys, or \tikzset to set certain keys. The <code> needs to move to the desired coordinate and stop. (Technically it just needs to save the desired dimensions in \pgf@x and \pgf@y). It can be accomplished with TikZ- or PGF-level commands.

Here is the implementation:

\makeatletter
\tikzset{/tikz/parallel cs/.cd,
    to line initial coordinate/.store in=\tikz@parallelcs@toA,
    to line final coordinate/.store in=\tikz@parallelcs@toB,
    on line initial coordinate/.store in=\tikz@parallelcs@onA,
    on line final coordinate/.store in=\tikz@parallelcs@onB,
    from coordinate/.store in=\tikz@parallelcs@from,
    to/.style args={#1--#2}{
        to line initial coordinate=#1,
        to line final coordinate=#2,
    },
    on/.style args={#1--#2}{
        on line initial coordinate=#1,
        on line final coordinate=#2,
    },
    from/.style={
        from coordinate=#1
    }
}
\tikzdeclarecoordinatesystem{parallel}{
    \tikzset{/tikz/parallel cs/.cd,#1}
    \tikz@scan@one@point\pgfutil@firstofone%
    (intersection of \tikz@parallelcs@from --$(\tikz@parallelcs@toA)!(\tikz@parallelcs@from)!90:(\tikz@parallelcs@toB)$ and \tikz@parallelcs@onA--\tikz@parallelcs@onB)%
    \relax
}
\makeatother

The \tikz@scan@one@point\pgfutil@firstofone pattern appears in many answers on this site. I don't grok it totally, but it allows a coordinate to be specified in TikZ language, then saves \pgf@x and \pgf@y just as we need. The rest of the code is a pgfkeyed-up version of the toy example.

Then you can use:

\begin{tikzpicture}
  \tikzset{point/.style={draw,circle,inner sep=0pt,outer sep=0pt,minimum width=2pt,fill}}
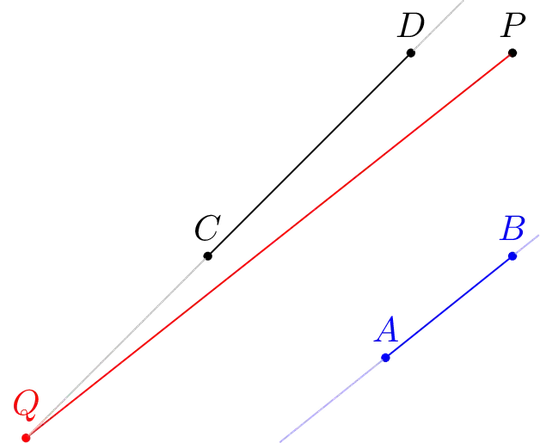
  \node[point,label=$P$] (P) at (3,3) {};
  \draw[blue] (0,0) node[point,label=$A$] (A) {} -- (3,1) node[point,label=$B$] (B) {};
  \draw       (0,1) node[point,label=$C$] (C) {} -- (2,3) node[point,label=$D$] (D) {};
  \draw[red] (P) -- (parallel cs:from=P,to=A--B,on=C--D) node [point,label=$Q$]{};
\end{tikzpicture}

As you can see, it even works when the projected point is not on the line segment:

\begin{tikzpicture}
  \tikzset{point/.style={draw,circle,inner sep=0pt,outer sep=0pt,minimum width=2pt,fill}}
  \node[point,label=$P$] (P) at (3,3) {};
  \draw[blue] (1.75,0) node[point,label=$A$] (A) {} -- (3,1) node[point,label=$B$] (B) {};
  \draw       (0,1) node[point,label=$C$] (C) {} -- (2,3) node[point,label=$D$] (D) {};
  \draw[red] (P) -- (parallel cs:from=P,to=A--B,on=C--D) node [point,label=$Q$] (Q) {};
  \draw[black!30!white] (Q) -- (C) 
      (D) -- (intersection of C--D and current bounding box.north west--current bounding box.north east);
  \draw[blue!30!white] 
      (intersection of A--B and current bounding box.south west--current bounding box.south east) -- (A)
      (B) -- (intersection of A--B and current bounding box.north east--current bounding box.south east);
\end{tikzpicture}

My original implementation used a TikZ let operation to specify the coordinate. It broke down when I tried some more complicated constructions. But Loop Space's answer takes it one level lower and it works.

\begin{tikzpicture}
    \tikzset{point/.style={draw,circle,inner sep=0pt,outer sep=0pt,minimum width=1pt,fill}}
    \node[point,label={90:$\scriptstyle P$}] (P) at (0,4) {};
    \node[point,label={180:$\scriptstyle B_{0}$}] (B-0) at (1,0) {};
    \node[point,label={0:$\scriptstyle A_1$}] (A-1) at (2,0) {};
    \node[point,label={180:$\scriptstyle B_{1}$}] (B-1) at (intersection of P--B-0 and 0,1--1,1) {};
    \draw (P) -- (B-0) (P) -- (A-1) (B-0) -- (A-1) -- (B-1);
    \foreach[remember=\i as \lasti (initially 1)] \i in {2,...,10} {
        \draw (B-\lasti) 
            -- (parallel cs:from=B-\lasti,to=B-0--A-1,on=P--A-1)
               node[point,label={0:$\scriptstyle A_{\i}$}] (A-\i) {}
            -- (parallel cs:from=A-\i,to=A-1--B-1,on=P--B-0)
               node[point,label={180:$\scriptstyle B_{\i}$}] (B-\i) {};
    }
\end{tikzpicture}

Very nice solution? Do you know if this will also work in pgfplots which I often also use as a base canvas (out of laziness) — daleif, Nov 19 '15 at 18:48
@daleif: I just tested it on a pgfplots canvas and it does seem to work, as well as it does without it. — Matthew Leingang, Nov 19 '15 at 19:13
@MatthewLeingang I've had a go at replacing your TikZ code by slightly lower level code which shouldn't clobber any options. If you still have the example around where it did the clobbering, could you test it? — Andrew Stacey, May 23 '17 at 19:12
@LoopSpace As "luck" (or laziness) would have it, I do have it lying around. And your implementation works with it! Here's the code. — Matthew Leingang, May 24 '17 at 19:12
In the fourth line, there is something wrong. Indeed ($(A)!(B)!(C)$) projects B on the segment connecting A and C — CLAUDE, Jul 05 '17 at 15:51

score 6 · Answer 2 · answered Nov 06 '15 at 15:01

6

Like this?

Code

\documentclass{standalone}
\usepackage{tikz}
\usetikzlibrary{calc}
\begin{document}
    \begin{tikzpicture}
       \coordinate (O) at (0,0); % Initial point of the line
       \coordinate (L) at (3,1); % End point of the line
       \draw[<->] (0,3) -- (0,0) -- (3,0);
       \draw (O) -- (L);
       \fill (2,2) coordinate (A) circle (2pt) node[right] {A};
       \draw[dashed] (A) -- ($(A -| 0,0)$);     
       \draw[dashed] let \p1=(O), \p2=(L), \p3=(A) in \pgfextra{\pgfmathsetmacro{\auxy}{\y3 - (\y2-\y1)/(\x2-\x1) * \x3}} (A) -- (0,\auxy pt);
    \end{tikzpicture}
\end{document}

answered Nov 06 '15 at 15:01

osjerick

6,970

Something like that, yes. – daleif Nov 06 '15 at 15:52
But simpler, right? – osjerick Nov 06 '15 at 16:39
In this case yes, not sure if it works in all coordinate system types – daleif Nov 06 '15 at 16:45

score 5 · Answer 3 · answered May 23 '17 at 19:11

5

This is a version of Matthew's code with the TikZ syntax replaced by more low-level code which oughtn't to clobber any options (however, I don't know what the example was that Matthew tested so I can't be sure).

\makeatletter
\tikzset{/tikz/parallel cs/.cd,
    to line initial coordinate/.store in=\tikz@parallelcs@toA,
    to line final coordinate/.store in=\tikz@parallelcs@toB,
    on line initial coordinate/.store in=\tikz@parallelcs@onA,
    on line final coordinate/.store in=\tikz@parallelcs@onB,
    from coordinate/.store in=\tikz@parallelcs@from,
    to/.style args={#1--#2}{
        to line initial coordinate=#1,
        to line final coordinate=#2,
    },
    on/.style args={#1--#2}{
        on line initial coordinate=#1,
        on line final coordinate=#2,
    },
    from/.style={
        from coordinate=#1
    }
  }

  \tikzdeclarecoordinatesystem{parallel}{
    \tikzset{/tikz/parallel cs/.cd,#1}
    \tikz@scan@one@point\pgfutil@firstofone%
    (intersection of \tikz@parallelcs@from --$(\tikz@parallelcs@toA)!(\tikz@parallelcs@from)!90:(\tikz@parallelcs@toB)$ and \tikz@parallelcs@onA--\tikz@parallelcs@onB)%
    \relax
  }
\makeatother

answered May 23 '17 at 19:11

Andrew Stacey

153,724
43
389
751

Now that I know yours works better than mine, I feel like yours should be the accepted one. Nice job. – Matthew Leingang May 24 '17 at 19:13
Alternatively, we could edit this code into your answer as it really belongs with it. I just wanted the rep ... – Andrew Stacey May 24 '17 at 22:00
I've done that. Thanks for improving my answer. I added my attempt at explaining what \tikz@scan@one@point\pgfutil@firstofone does. Do I have it right? – Matthew Leingang May 25 '17 at 15:02
1

@MatthewLeingang Maybe you should ask a question about it so I can get more rep ... I mean, so that others can benefit from understanding what it does. – Andrew Stacey May 25 '17 at 20:09
Gunning for 100K, are you? :-) – Matthew Leingang May 26 '17 at 02:27
@MatthewLeingang Am I near 100k? I really hadn't noticed ... – Andrew Stacey May 26 '17 at 05:34
@LoopSpace, is it possible to adapt this solution to specify either a length or the projection line? Something like (parallel cs: to=A--B, from=P, length=2cm). I have absolutely no clue how to do that... – Guilherme Zanotelli Nov 27 '18 at 17:09

tikz projection parallel to given line

3 Answers3

Code