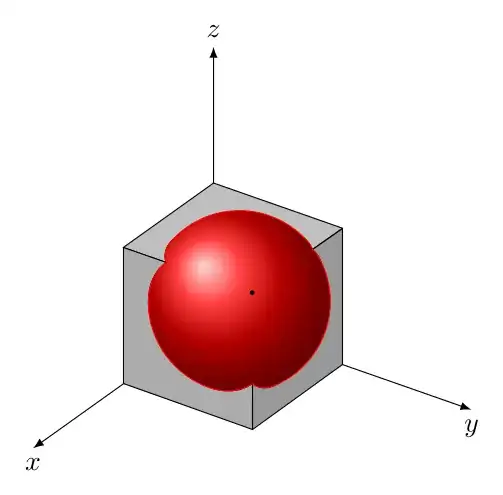
The problem is the same as explained in my previous question: How to fill an area outside circles?. The only difference that now I need to fill the green area in three-dimensional space, i.e., the area outside both spheres but inside the cube.
At the moment I have:
\documentclass[tikz,margin=15pt]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.10}
\usetikzlibrary{pgfplots.fillbetween,backgrounds}
\begin{tikzpicture}
\begin{axis}[
width=8cm, height=8cm,
xmin=-0.2, xmax=1.2, ymin=-0.2, ymax=1.2, zmin=-0.2, zmax=1.2,
every tick label/.append style={font=\tiny},
xlabel = {$ x_1 $}, ylabel = {$ x_2 $}, zlabel = {$ x_3 $},
xtick={0,0.167,0.33,0.5,0.66,0.833,1.0},
xticklabels={$0$,$\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{2}$,$\frac{2}{3}$,$\frac{5}{6}$,$1$},
ytick={0,0.167,0.33,0.5,0.66,0.833,1.0},
yticklabels={$0$,$\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{2}$,$\frac{2}{3}$,$\frac{5}{6}$,$1$},
ztick={0,0.167,0.33,0.5,0.66,0.833,1.0},
zticklabels={$0$,$\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{2}$,$\frac{2}{3}$,$\frac{5}{6}$,$1$},
enlargelimits=0.05,
view={15}{10},
]
% Draw hyper-rectangle (cube)
\addplot3[style=very thick,mark=none,color=blue] coordinates {
(0,0,0) (1,0,0) (1,1,0)
(0,0,1) (1,0,1) (1,1,1) (0,1,1) (0,0,1)
(0,0,0) (0,0,1)
(1,0,0) (1,0,1)
(1,1,0) (1,1,1)
};
% Draw imaginary edges
\addplot3[style=dashed,style=thick,mark=none,color=blue] coordinates {
(1,1,0) (0,1,0) (0,0,0)
(0,1,0) (0,1,1)
};
% Draw sampling points
\addplot3[only marks,mark=*,nodes near coords,point meta=explicit symbolic, color=blue, opacity=0.75,font=\scriptsize] coordinates {
(1/3,1/3,1/3) [(1)]
(2/3,2/3,2/3) [(2)]
};
% Draw the first sphere, based on:
% https://tex.stackexchange.com/questions/124916/draw-sphere-pgfplots-with-axis-at-center
\addplot3[%
opacity = 0.3,
mesh,
red,
z buffer = sort,
samples = 21,
variable = \u,
variable y = \v,
domain = 0:180,
y domain = 0:360,
] ({0.33 + 0.58*cos(u)*sin(v)}, {0.33 + 0.58*sin(u)*sin(v)}, {0.33 + 0.58*cos(v)});
% Draw the second sphere
\addplot3[%
opacity = 0.3,
mesh,
red,
z buffer = sort,
samples = 21,
variable = \u,
variable y = \v,
domain = 0:180,
y domain = 0:360,
] ({0.66 + 0.58*cos(u)*sin(v)}, {0.66 + 0.58*sin(u)*sin(v)}, {0.66 + 0.58*cos(v)});
% Draw diameter
\addplot3[color=black,very thick] coordinates { (1/3,1/3,1/3) (0,0,0) } node[pos=0.5, yshift=8pt, sloped] { $\delta$};
% TODO: Fill the area outside both spheres but inside the cube
\end{axis}
\end{tikzpicture}
\end{document}
I am wondering if there is a similar way to @Alenanno proposed solution for 2-D case.