pgfplots exp(-pow(deg(x),2) on domain 0:2*pi

Question

This code throws me an error, "Dimension too large". I cannot figure out how to fix. I just measured the source of my global error, this short snippet:

\begin{tikzpicture} 
\begin{axis}[axis lines=none,no markers,samples=50,grid=both]
\addplot3[mesh, domain=0:2*pi] {exp(-pow(deg(x),2))}; 
\end{axis}
\end{tikzpicture}

I need to plot this function on that domain. Is there a way to do it so? Mathematical is meant to do like: $$e^{-deg(x)^2}$$ (btw I don't know, whats deg(**) for?)

My whole aim is: Plotting the Klein Bottle with tikz or pgfplots.

2*pi in degrees will give 360, squared gives 129600, and exp(-129600) is a very very small number, so you will run into an underflow. Besides, I doubt that you really want to plot this function since it is zero most of the time (exp(-x) soon drops to values close to zero). — gernot, Jan 28 '17 at 18:48
you're right. I'll use another parametrisation, like https://en.wikipedia.org/wiki/Klein_bottle#Bottle_shape this works fine — Shalec, Jan 28 '17 at 19:09
So is your question answered now? If yes, you could either consider if my answer fits your needs as well and then accept it or we close it, so the question is of the "still unanswered" list. — Stefan Pinnow, Jan 30 '17 at 18:18

Stefan Pinnow · Accepted Answer · 2017-01-28T19:50:05.043

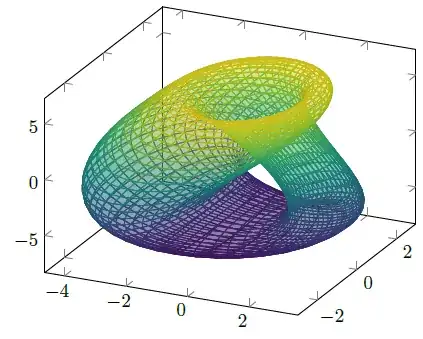
I use the equations and parameters given at the German Wiki entry for the "Klein bottle" which gives the following result. (In addition I used LuaLaTeX and the Lua backend of PGFPlots which calculates the result quite fast.)

% used PGFPlots v1.14
\RequirePackage{luatex85}
\documentclass[border=5pt]{standalone}
\usepackage{pgfplots}
    \pgfplotsset{
        % use this `compat' level or higher to use the Lua backend
        compat=1.12,
        % used equations and parameters from
        % <https://de.wikipedia.org/w/index.php?title=Kleinsche_Flasche&oldid=160519755#Beschreibung_im_3-dimensionalen_Raum>
        /pgf/declare function={
            b = 2;
            h = 6;
            r(\u) = 2 - cos(\u);
%            x(\u,\v) = b * (1 - sin(\u)) * cos(\u);
%                       + r(\u) * cos(\v) * (2 * exp( -(\u/2 - pi)^2 ) - 1);
%            y(\u,\v) = r(\u) * sin(\v);
%            z(\u,\v) = h * sin(\u)
%                       + 0.5 * r(\u) * sin(\u) * cos(\v) * exp( -(\u-3*pi/2)^2 );
        },
    }
\begin{document}
    \begin{tikzpicture}
        \begin{axis}[
%            axis lines=none,
            % use radians as input for the trigonometric functions
            % (this avoids converting the numbers to `deg' format first)
            trig format plots=rad,
            domain=0:2*pi,
            samples=50,
            % change variables from `x' and `y' to `u' and `v'
            variable=u,
            variable y=v,
            colormap/viridis,
        ]
            \addplot3 [
%                mesh,
                % I use suf here, because it just looks better ;)
                surf,
                z buffer=sort,
                fill opacity=0.35,
            ] (
                % unfortunately these give an error ...
%                {x(u,v)},
%                {y(u,v)},
%                {z(u,v)},
                % ... so we write them directly
                {b * (1 - sin(u)) * cos(u) + r(u) * cos(v) * (2 * exp( -(u/2 - pi)^2 ) - 1)},
                {r(u) * sin(v)},
                {h * sin(u) + 0.5 * r(u) * sin(u) * cos(v) * exp( -(u - 3 * pi / 2)^2 )}
            );
        \end{axis}
    \end{tikzpicture}
\end{document}

I did it too. But this was throwing me an error: exp( -(u/2 - pi)^2 ) How did u solved this? Maybe this is the solution about my prob: trig format plots=rad, — Shalec, Jan 31 '17 at 08:40
I am not 100% sure if I understand you right, but I guess that you didn't change the variable to u (variable=u) and thus got an error that the "function" `u' is unknown. Your suggestion shouldn't change anything, because you don't use a trigonometric function in the your provided equation. — Stefan Pinnow, Jan 31 '17 at 09:34
You mean the image with "computation"? Make a screenshot of the result and add it using the "Image" button when you edit your answer. Alternatively you can press CTRL+G to pop up the "Image" dialog. — Stefan Pinnow, Feb 01 '17 at 16:28
Would you mind accepting this (or your) answer if your question is solved so your question gets of the "not accepted" list? Many thanks. — Stefan Pinnow, Feb 12 '17 at 18:40

score 0 · Answer 2 · edited Feb 01 '17 at 16:26

This did it.

\pgfplotsset{%
        colormap = {black}{%
            color(0cm)  = (black);%
            color(1cm) = (black)}%
    }

\begin{tikzpicture}
\def\rotation{0}

    \begin{axis}[axis lines=none, rotate around={\rotation:(current axis.origin)}]
    \addplot3[mesh, z buffer=sort,domain=0:180, domain y=0:360, samples=41, samples y=25,   point meta=x] 
        (
        {-2/15 * cos(x) * (
            3*cos(y) - 30*sin(x) 
          + 90 *cos(x)^4 * sin(x) 
          - 60 *cos(x)^6 * sin(x)  
          + 5 * cos(x)*cos(y) * sin(x))
         },
         {-1/15 * sin(x) * (3*cos(y) 
          - 3*cos(x)^2 * cos(y) 
          - 48 * cos(x)^4*cos(y) 
          + 48*cos(x)^6 *cos(y) 
          - 60 *sin(x) 
          + 5*cos(x)*cos(y)*sin(x) 
          - 5*cos(x)^3 * cos(y) *sin(x) 
          - 80*cos(x)^5 * cos(y)*sin(x) 
          + 80*cos(x)^7 * cos(y) * sin(x))
         },
        {2/15 * (3 + 5*cos(x) *sin(x))*sin(y)}      
        );
    \end{axis}
\end{tikzpicture}

pgfplots exp(-pow(deg(x),2) on domain 0:2*pi

2 Answers2

Linked