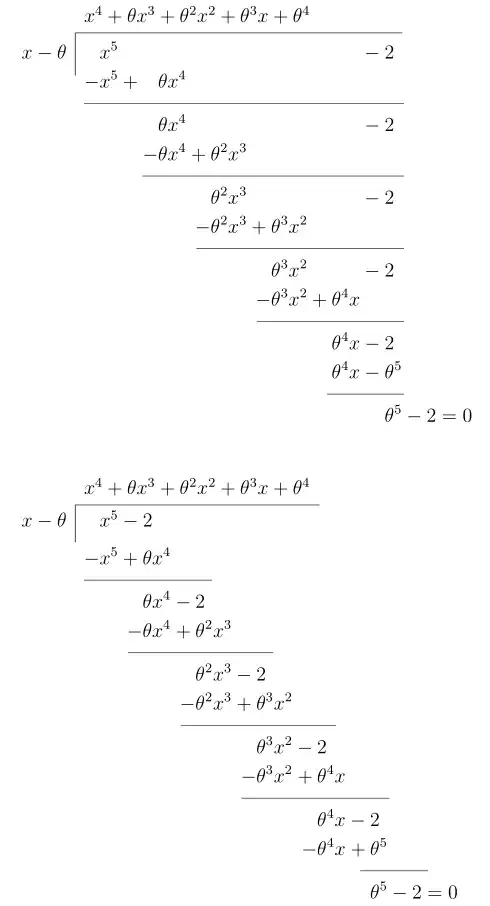Raising the vertical bar - polynomial division

Question

I've tried to create a polynomial long division using several approaches such as the ones outlined in:

How to draw polynom division?

Polynomial Long Division Using Polynom

Better way to display long division?

With limited success. So I tried the naive approach which looks quite good as can be seen in the diagram, however, the vertical bar \big| is spaced too far down. If possible I'd like it to move up and ideally touch the horizontal long division bar.

How can I accomplish this?

\documentclass[12pt,a4paper]{article}

\usepackage[fleqn]{amsmath}
\usepackage[normalem]{ulem}

\begin{document}
\begin{equation*}
\begin{split}
&\uline{x^4  + \theta x^3 + \theta^2x^2 + \theta^3x + \theta^4}\\
x - \theta \ \big| & x^5 -2\\
& \uline{x^5 - \theta x^4} \\
& \theta x^4 - 2\\
& \uline{\theta x^4 - \theta^2x^3}\\
& \theta^2x^3 - 2\\
& \uline{\theta^2x^3 - \theta^3x^2}\\
& \theta^3x^2 - 2\\
&\uline{\theta^3x^2 - \theta^4x}\\
& \theta^4x - 2\\
& \uline{\theta^4x - \theta^5}\\
& \theta^5 - 2  \ \ \ \ \ \ \ \ \ =  \ \ \ 0
\end{split}
\end{equation*}

\end{document}

Which produces:

Answer 1

I propose one of these layouts, based on array, alignedat and booktabs:

\documentclass[12pt,a4paper]{article}
\usepackage{array}
\usepackage[fleqn]{amsmath}
\usepackage{booktabs}

\begin{document}

\begin{equation*}\setlength\extrarowheight{3pt}
  \begin{array}{rl}
    & x⁴ + θx³ + \theta²x² + \theta³x + \theta⁴ \\
    \cmidrule(r{4em}){2-2}\addlinespace[-\dimexpr\belowrulesep + \cmidrulewidth]
    \multicolumn{1}{r!{\rule[-2ex]{0.4pt}{5ex}}}{x - θ} & \begin{alignedat}[t]{8}
      & \phantom{-}x⁵ & & & & & & & & & {} - {} & 2 \\%[1ex]
    &{-} x⁵ + {}& & θx⁴ \\
    \cmidrule(r{3.5em}){1-12}
      & & & θx⁴ & & & & & & & {}-{} & 2 \\
    & &- & θx⁴ & {} + {}&\theta²x³\\
    \cmidrule(r{3.5em}){3-12}
      & & & & & \theta²x³ & & & & & {}-{} & 2 \\
    & & & &- & \theta²x³ & {} + {} & \theta³x²\\
    \cmidrule(l{0.5em}r{3.5em}){5-12}
      & & & & & & & \theta³x² & & & {}-{} & 2 \\
    & & & & & & -&\theta³x² & {} + {} & \theta⁴x\\
    \cmidrule(l{0.5em}r{3.5em}){7-12}
      & & & & & & & & & \theta⁴x & {}-{} & 2 \\
      & & & & & & & & & \theta⁴x & {}-{} & \theta⁵ \\
    \cmidrule(l{1em}r{3.5em}){9-12}
      & & & & & & & & & & & \theta⁵ - 2 = 0
    \end{alignedat}
  \end{array}
\end{equation*}

\begin{equation*}\setlength\extrarowheight{3pt}
  \begin{array}{rl}
    & x⁴ + θx³ + \theta²x² + \theta³x + \theta⁴ \\
    \cmidrule(r{7.5em}){2-2}\addlinespace[-\dimexpr\belowrulesep + \cmidrulewidth]
    \multicolumn{1}{r|}{x - θ} &
    \phantom{-}x⁵ - 2\\[1ex]
    & \begin{alignedat}[t]{8}
    -&x⁵ &{}+{} & θx⁴ \\
    \cmidrule(r{1em}){1-6}
    & & & θx⁴ & {}-{} & 2\\
    & & -& θx⁴ & {} + {}&\theta²x³\\
    \cmidrule(lr{1em}){3-8}
    & & & & & \theta²x³ & {}-{} & 2\\
    & & & &- & \theta²x³ & {} + {} & \theta³x²\\
    \cmidrule(lr{0.5em}){5-10}
    & & & & & & & \theta³x² & {} - {} & 2\\
    & & & & & & - &\theta³x² & {} + {} & \theta⁴x\\
    \cmidrule(lr{3.5em}){7-12}
      & & & & & & & & & \theta⁴x & {}-{} & 2 \\
      & & & & & & & & - & \theta⁴x & {} + {} & \theta⁵ \\
    \cmidrule(l{-0.5em}r{1.5em}){12-12}
      & & & & & & & & & & & \theta⁵ - 2 = 0
    \end{alignedat}
  \end{array}
\end{equation*}

\end{document} 

Answer 2

Polynomial devision is (sometimes at least) clearer if you align the monomial terms, so here I take three cells per monomial r for the coefficient, l for the power of x and c for the binary operator.

Touching the line is achieved with \vline which is the segment latex usually uses for vertical rules in tables as specified by a | in the array or tabular preamble.

\documentclass[12pt,a4paper]{article}
\usepackage{array}
\usepackage[fleqn]{amsmath}


\begin{document}

\begin{equation*}
\setlength\arraycolsep{0pt}
\setlength\extrarowheight{2pt}
\begin{array}{r@{\;}c@{\;}*{10}{rl>{{}}c<{{}}}}
&&&&&&x^4&  +& \theta&x^3& +& \theta^2&x^2& +& \theta^3&x& +& \theta^4\\
\cline{2-18}
x - \theta &\vline& &x^5 &-&&&&&&&&&&&&&2\\
&& &x^5 &-& \theta &x^4 \\
\cline{3-18}
&&&&& \theta &x^4 &-&&&&&&&&&& 2\\
&&&&& \theta &x^4 &-& \theta^2&x^3\\
\cline{6-18}
&&&&&&&& \theta^2&x^3 &-& &&&&&&2\\
&&&&&&&& \theta^2&x^3 &-& \theta^3&x^2\\
\cline{9-18}
&&&&&&&&&&& \theta^3&x^2 &-&&&& 2\\
&&&&&&&&&&&\theta^3&x^2 &-& \theta^4&x\\
\cline{12-18}
&&&&&&&&&&&&&& \theta^4&x &-& 2\\
&&&&&&&&&&&&&& \theta^4&x &-& \theta^5\\
\cline{15-18}
&&&&&&&&&&&&&&&&& \theta^5 -2  &=  0
\end{array}
\end{equation*}

\end{document}

Answer 3

Using \tabluar, \vline and \cline, here is another example for polynomial division x[n]=[1,-1,0,0,0,0,-1,1] / x_1[n]=[1,1,1,1,1,1], where the sequences corresponds to coefficients of the polynomials x[n] and x_1[n]. The columns are sized (p{0.15cm}) so that the \vline can connect properly to the top and bottom lines. \tiny font is used here to enable it fit into one column of a 2-column paper, if a bigger font is used the column sizes should be increased from p{0.15cm}. This method can also be used to write deconvolution or inverse Z-transform using the long division approach. I hope someone finds it useful.

{\tiny
\begin{center}
\begin{tabular}{p{0.15cm}p{0.15cm}p{0.15cm}p{0.15cm}p{0.15cm}p{0.1cm}p{0.1cm}p{0.15cm}p{0.15cm}p{0.15cm}p{0.15cm}p{0.15cm}p{0.15cm}p{0.15cm}p{0.15cm}}
  &   &   &   &   &   & 1 & -2  & 1 &   &   &   &   & \\\cline{7-14}
 1 & 1 & 1 & 1 & 1 & $1 \ \ \ \ \ \ \vline$ & 1 & -1 & 0  & 0  & 0  & 0  & 1  & 1\\\cline{1-6}
    &   &   &   &   &   & 1 & 1 & 1 & 1 & 1 &  1 &   & \\\cline{7-14}
    &   &   &   &   &   &   & -2 & -1 & -1 & -1 & -1 & -1 & \\
    &   &   &   &   &   &   & -2 & -2 & -2 & -2 & -2 & -2 & \\\cline{8-14}
    &   &   &   &   &   &   &   & 1 & 1 & 1 & 1 & 1 & 1\\
    &   &   &   &   &   &   &   & 1 & 1 & 1 & 1 & 1 & 1\\\cline{9-14}
    &   &   &   &   &   &   &   & 0 & 0 & 0 & 0 & 0 & 0\\   
\end{tabular}
\end{center}
}