Here's how you can debug situations like this by yourself. If you add \tracingparagraphs=1 before this paragraph and run xelatex, you see the following output in the log file:
@firstpass
[]\TU/LatinModernRoman(0)/m/n/10 By Taylor’s theorem, for any $[] [] []$, there is a least $[][][][] [] []$ s.t. $[][][] [] [] []
@\penalty via @@0 b=986 p=9500 d=91252016
@@1: line 1.0 t=91252016 -> @@0
[] [] [][][][][][]$.
@\par via @@1 b=0 p=-10000 d=10100
@@2: line 2.2- t=91262116 -> @@1
If you run it with lualatex, the output is a bit different, but the relevant numbers are the same:
@firstpass
[]\TU/LatinModernRoman(0)/m/n/10 By Tay-lor’s the-o-rem, for any $\TU/XITSMath(0)/m/n/10 > 0$\TU/LatinModernRoman(0)/m/n/10 , there is a least $[]\TU/XITSMath(0)/m/n/10 () > 0$ \TU/LatinModernRoman(0)/m/n/10 s.t. $\TU/XITSMath(0)/m/n/10 || < ⟹
@\penalty via @0 b=986 p=9500 d=91252016
@@1: line 1.0 t=91252016 -> @0
[] ≤ []()[]$\TU/LatinModernRoman(0)/m/n/10 .
@\par via @1 b=0 p=-10000 d=10100
@@2: line 2.2- t=91262116 -> @1
A tutorial on how to read this is in The TeXbook, pages 98–99. (“The line-break data looks pretty scary at first, but you can learn to read it with a little practice; this, in fact, is the best way to get a solid understanding of line breaking.”) (See also sections around 846/856 of the TeX program, which you can see with texdoc tex.)
- The lines beginning with
@@ are feasible breakpoints: the only places that can be reached without ever having the badness greater than the \tolerance (or \pretolerance, in the first pass). [In this example, there is only one feasible breakpoint for line 1: after the implies sign.]
- The rest of the information on a such a line pertains to the best way of getting to that breakpoint: after the line number, the suffix
.0 denotes a "very loose" (stretch with badness ≥ 100) line, .1 denotes a "loose" line (stretch with 100 > badness ≥ 13), .2 denotes a "decent" line (badness ≤ 12), and .3 denotes a "tight" line (shrink with badness ≥ 13). [In this example, the .0 denotes that it was very loose.]
- The suffix
- (after one of .0, .1, .2, .3) means that either the line ends with a discretionary break or it is the last line of the paragraph.
- The
t= value is the total demerits accumulated from the beginning of the paragraph to that breakpoint.
- Each line beginning with
@ (a single one, not @@) is a potential way to reach the @@ breakpoint that comes after it (namely: which previous breakpoint you could choose, to end at that breakpoint). So on each such line, after the @ there is one of \par, \penalty, \discretionary, \kern, \math (or nothing), followed by via @@ (seems to be just via @ in LuaTeX above, not sure why they changed it or even whether it's intentional) and then the previous breakpoint.
- On each such line, next there is the actual badness with
b= (corresponding to how much the glue had to stretch/shrink) (note: b=* means that the badness was infinite (>10000): The TeXbook says this happens when “an infeasible breakpoint had to be chosen because there was no feasible way to keep total demerits small”), the penalty with p=, and, computed from them, the demerits with d=.
So you can see in your case from output above that there was only one way to reach the only feasible breakpoint, and that it resulted in a badness of 986. As badness is roughly 100(t/s)^3, this gives t/s ≈ ∛(986/100) ≈ 2.14: the glue on the line had to be stretched by more than twice its specified stretchability.
Normally TeX won't even consider such breakpoints (as the default is \pretolerance=100 (for the first pass, without hyphenation) and \tolerance=200), and will instead simply give up and produce an overfull box (which can be typographically much worse!), but in this case with \pretolerance set so high, TeX simply goes ahead.
Anyway, to answer when TeX prints a warning about underfull boxes: TeX warns about all lines with badness greater than \hbadness. So you can specify \hbadness=985 (or lower; the default is 1000) to get a warning in this case.
Finally, I don't agree with the view that setting \tolerance high is a bad idea. All it does is allow TeX to consider worse lines: a high tolerance can mean the difference between having overfull boxes (the other lines will be beautiful, but the overall output will be worse) and not having them (some lines worse, but fewer awful overfull boxes). The TeXbook also says something similar, on page 30:
…the problem of breaking a paragraph into approximately equal lines. When the lines are relatively wide, TeX will almost always find a good solution. But otherwise you will have to figure out some compromise, and several options are possible. Suppose you want to ensure that no lines have badness exceeding 500. Then you could set \tolerance to some high number, and \hbadness=500; TeX would not produce overfull boxes, but it would warn you about the underfull ones. Or you could set \tolerance=500; then TeX might produce overfull boxes. If you really want to take corrective action, the second alternative is better, because you can look at an overfull box to see how much sticks out; it becomes graphically clear what remedies are possible. On the other hand, if you don’t have time to fix bad spacing—if you just want to know how bad it is—then the first alternative is better, although it may require more computer time.
By the way, as for a rewrite, my preference would go in the opposite direction as in Henri Menke's answer: to move from overly concise notation towards readable prose. Keeping all your parameters and packages exactly as they are, simply changing "s.t." to "such that" gets badness down from 986 to 438, dropping the \implies gets it down to 269, and introducing more words gets badness down to 1 and even 0:
 (^ first-line badness 986, 438, 269, 1, 0 respectively)
(^ first-line badness 986, 438, 269, 1, 0 respectively)



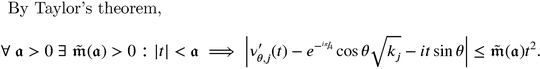
\toleranceto an insane 7000! (default is 200) – Henri Menke Jun 11 '17 at 23:02s.t.looks huge but to me it appears as if there's an inter-sentence space and not an inter-word one. – yo' Jun 11 '17 at 23:43amsmathis included afterunicode-math, as in\documentclass{article} \usepackage{unicode-math} \usepackage{amsmath} \begin{document} $\sin \cos$ \end{document}-- but not if the packages are included in the other order. – ShreevatsaR Jun 13 '17 at 13:57