How to generate a heat diagram?

Question

I was recently reading a paper and I came across this diagram in the paper:

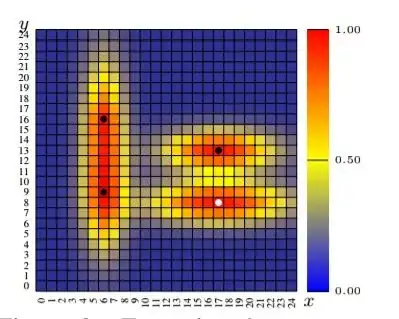
It basically shows the precision of an approximation algorithm as x and y varies. Does anyone know what sort of package this is?

Impossible to say exactly what software was used to make that (ask the authors of the paper if that is important), but you can do similar stuff with pgfplots. For example, https://tex.stackexchange.com/questions/388808 — Torbjørn T., Aug 30 '17 at 21:23
See also https://tex.stackexchange.com/questions/264182/drawing-a-really-large-binary-matrix-as-colored-grid — John Kormylo, Aug 31 '17 at 01:29
I saw both links but they gives answers using files created by programs or values stored in a matrix. I think the request of a heat diagram like the above is to calculate and use the distance of two centers. Something like this is the way physics works too (May be the distance of just one hot point is enough in physics but makes thinks more difficult in practice because of the flow that creates something like ellipses). For these reasons I think my answer will be useful for such kind of diagrams without matrices but just heat centers. — koleygr, Aug 31 '17 at 01:37

score 2 · Answer 1 · answered Aug 31 '17 at 01:26

Here is the idea of it:

You have to create some ellipses (they have two centers) and calculate the addition of the distances of each ellipse center. If any point (in general) has a distance smaller than a given value you color the box corresponding to that point with a color (red for closer point, orange for more distance etc)

The code to do something like this is here:

\documentclass{standalone}
\usepackage{tikz}
\usepackage{xcolor}
\usetikzlibrary{calc}

\xdef\YintSquares{70}
\xdef\XintSquares{70}
\xdef\factor{20}
\xdef\numEclipse{3}
\xdef\numColors{5}
\xdef\DefCol{blue}

\def\AddFCenter#1#2#3{
\xdef\tempFX{#2}
\global\expandafter\let\csname CenterFX#1\endcsname\tempFX
\xdef\tempFY{#3}
\global\expandafter\let\csname CenterFY#1\endcsname\tempFY}

\def\AddSCenter#1#2#3{
\xdef\tempFX{#2}
\global\expandafter\let\csname CenterSX#1\endcsname\tempFX
\xdef\tempFY{#3}
\global\expandafter\let\csname CenterSY#1\endcsname\tempFY}

\AddFCenter{1}{15}{24}
\AddSCenter{1}{16}{41}
\AddFCenter{2}{47}{53}
\AddSCenter{2}{50}{59}
\AddFCenter{3}{50}{30}
\AddSCenter{3}{44}{28}

\def\AddColorDistance#1#2#3{
\xdef\MyDist{#2}
\xdef\MyColor{#3}
\global\expandafter\let\csname UntilDistance#1\endcsname\MyDist
\global\expandafter\let\csname ColorAtDistance#1\endcsname\MyColor
}

\AddColorDistance{1}{17}{red}
\AddColorDistance{2}{19}{red!70!orange}
\AddColorDistance{3}{23}{orange}
\AddColorDistance{4}{27}{orange!70!yellow}
\AddColorDistance{5}{30}{yellow}

\xdef\DrawLW{0.01mm}




\pgfmathsetmacro\circleRarious{1/\factor/sqrt(2)/2}


\begin{document}

\begin{tikzpicture}
   \foreach \x in {0,...,\XintSquares}
   {
      \foreach \y in {0,...,\YintSquares}{
         \foreach \n in {1,...,\numEclipse}{
            \pgfmathsetmacro\distF{int(sqrt((\y-\csname CenterFY\n\endcsname)^2+(\x-\csname CenterFX\n\endcsname)^2))}
            \pgfmathsetmacro\distS{int(sqrt((\y-\csname CenterSY\n\endcsname)^2+(\x-\csname CenterSX\n\endcsname)^2))}
            \pgfmathsetmacro\dist{int(sqrt((\y-\csname CenterFY\n\endcsname)^2+(\x-\csname CenterFX\n\endcsname)^2)
            +sqrt((\y-\csname CenterSY\n\endcsname)^2+(\x-\csname CenterSX\n\endcsname)^2))}
            \ifcsname ValueOf\x And \y\endcsname
               \pgfmathsetmacro\tempbef{\csname ValueOf\x And \y\endcsname}
               \ifnum\tempbef<\dist
               \relax
               \else
               \global\expandafter\let\csname ValueOf\x And \y\endcsname\dist
               \fi
           \else
               \global\expandafter\let\csname ValueOf\x And \y\endcsname\dist
            \fi
            \ifnum\distF=0
            \global\expandafter\let\csname TrueCenterX\x Y\y\endcsname\distF
            \else
               \ifnum\distS=0
               \global\expandafter\let\csname TrueCenterX\x Y\y\endcsname\distS
               \else
               \relax
               \fi
            \fi
         }
         \xdef\curVal{\csname ValueOf\x And \y\endcsname}
         \ifcsname TrueCenterX\x Y\y\endcsname
            \xdef\OnCenter{1}
         \else
            \xdef\OnCenter{0}
         \fi
           \ifnum\OnCenter=1
              \draw[line width=\DrawLW,fill=red] ($(\x/\factor,\y/\factor)$)--($({(\x+1)/\factor},\y/\factor)$)--($({(\x+1)/\factor},{(\y+1)/\factor})$)--($(\x/\factor,{(\y+1)/\factor})$)--cycle;
              \draw[,fill=black] ($({(\x/\factor+(\x+1)/\factor)/2},{(\y/\factor+(\y+1)/\factor)/2})$) circle (\circleRarious);
            \else
              \xdef\BoolFillDefault{1}
              \foreach \col in {1,...,\numColors}{
              \xdef\valforCol{\csname UntilDistance\col\endcsname}
              \ifnum\curVal<\valforCol

                 \xdef\Col{\csname ColorAtDistance\col\endcsname}
                 \draw[line width=\DrawLW,fill=\Col] ($(\x/\factor,\y/\factor)$)--($({(\x+1)/\factor},\y/\factor)$)--($({(\x+1)/\factor},{(\y+1)/\factor})$)--($(\x/\factor,{(\y+1)/\factor})$)--cycle;
                 \xdef\BoolFillDefault{0}
                 \breakforeach              
              \fi
              }
             \ifnum\BoolFillDefault=1
                \draw[line width=\DrawLW,fill=\DefCol] ($(\x/\factor,\y/\factor)$)--($({(\x+1)/\factor},\y/\factor)$)--($({(\x+1)/\factor},{(\y+1)/\factor})$)--($(\x/\factor,{(\y+1)/\factor})$)--cycle;
             \fi
          \fi
      }
   }
\end{tikzpicture}


\end{document}

And the result is:

The distance for the colors that I used is common for all ellipses and this means that you have to draw οverlapping ellipses for distances of centers over your distance.

If someone finds my answer useful and wants... I can fix it to use separate value for each ellipse "temperature" or give him instructions to do it — koleygr, Aug 31 '17 at 01:48

How to generate a heat diagram?

1 Answers1