What am I doing wrong?
\documentclass{amsart}
\usepackage{amssymb,amsmath,latexsym,times,color}
\newtheorem*{theorem*}{Theorem}
\newtheorem{theorem}{Theorem}
\newtheorem{lemma}[theorem]{Lemma}
\begin{document}
Question Number 3
\begin{theorem*}
Since a and b are positive numbers, then $$\frac{a}{b}$$ and $$\frac{a+2b}{a}$$ are positive integers.
\end{theorem*}
\begin{proof}
Case 1: If $$\frac{a}{b}\leq 2$$ then $$min{$$\frac{a}{b}$$,$$\frac{a+2b}{a}$$}\leq\frac{a}{b}\leq 2$$
Thus $$min{\frac{a}{b}$$,$$\frac{a+2b}{a}$$}\leq 2$$
Case 1: If $$\frac{a}{b}\leq 2$$ then $$min{$$\frac{a}{b}$$,$$\frac{a+2b}{a}$$}\leq\frac{a}{b}\leq 2$$
Thus min{$$\frac{a}{b}$$,$$\frac{a+2b}{a}$$}\leq 2
Case 2: If $$\frac{a}{b}>2$$ then $$\frac{b}{a}<(1/2)$$
Since $$\frac{a+2b}{a}= \frac{a}{a} + \frac{2b}{a}$$ which also means it is < 1+2*(1/2)
Thus $$\frac{a+2b}{a}<2$$
so $$min{$$\frac{a}{b}$$,$$\frac{a+2b}{a}$$}\leq\frac{a+2b}{a}<2$$
Hence from both sides we have min{$$\frac{a}{b}$$,$$\frac{a+2b}{a}$$}\leq 2
If you do this again with opposite inequalities you will get:
Case 1: If $$\frac{a}{b}\leq2$$ then \frac{b}{a}\geq (1/2)
Since $$\frac{a+2b}{a}= 1+\frac{2b}{a}\geq 1+2*(1/2)= 2$$ so \frac{a+2b}{a}\geq 2
thus $$max{\frac{a}{b},\frac{a+2b}{a}}\geq \frac{a+2b}{a}\geq 2$$ which simplifies to:
$$max{\frac{a}{b},\frac{a+2b}{a}}\geq 2$$
Case 2: If $$\frac{a}{b}>2$$ then $$max{\frac{a}{b},\frac{a+2b}{a}}\geq \frac{a}{b}>2$$
This means:
$$max{\frac{a}{b},\frac{a+2b}{a}}>2$$
From both cases we get: $$max{\frac{a}{b},\frac{a+2b}{a}}\geq 2$$
Since both sets of inequalities are true, we obtain:
$$min{\frac{a}{b},\frac{a+2b}{a}}\leq 2\leq max{\frac{a}{b},\frac{a+2b}{a}}$$
\end{proof}
\end{document}


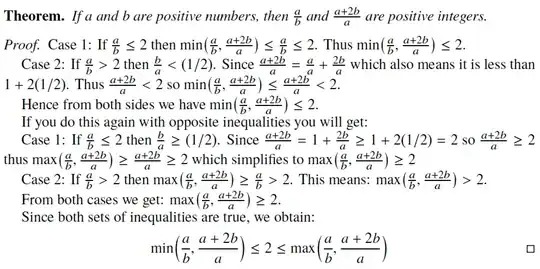
\begin{document}and\end{document}. – TeXnician Sep 11 '17 at 05:02latexsympackage shouldn't be loaded for documents more recent than 1995, especially as you're loading the much more up-to-dateamssymbpackage. – Mico Sep 11 '17 at 06:00\documentclasswill be undefined. – David Carlisle Sep 11 '17 at 06:34