Only changing the limits for \sum:
You could use the internal conditional \if@display from amsmath to test whether or not \limits should be inserted.
Below, I'm redefining \sum by adding \if@display\limits\fi to its definition.
\documentclass{article}
\usepackage{amsmath}
\makeatletter %% <- make @ usable in command names
\renewcommand*\sum{\DOTSB\sum@\if@display\limits\fi}
\makeatother %% <- revert @
\begin{document}
Lorem $e^{\sum_{n=1}^\infty \frac1n}$ ipsum
\[
e^{\sum_{n=1}^\infty \frac1n}
\]
\begin{align}
e^{\sum_{n=1}^\infty \frac1n}&
\\
&e^{\sum_{n=1}^\infty \frac1n}
\end{align}
Lorem $e^{\sum_{n=1}^\infty \frac1n}$ ipsum
\end{document}

This can be adapted to work for other operators like \prod, \coprod, \bigcup, \bigotimes, etc. by changing \sum@ in the obvious way.
If you have an operator, say \myoperator, for which \myoperator@ does not exist, you can create it with
\makeatletter %% <- remove if you paste the next line between \makeatletter/-other
\let\myoperator@\myoperator
\makeatother %% <- remove this one too, then
and proceed as above.
Alternative:
I originally had another solution that I was quite happy with that uses \everydisplay.
The contents of this register is inserted at the start of every display math environment and I used it to redefine \sum by including \limits.
It works without amsmath (which everyone should use), but apart from that I think it's superceded by the solution above.
Anyway, here it is.
The following would replace the \makeatletter-\makeatother block above.
\makeatletter %% <- make @ usable in command names
\let\sum@beforelimitmodification\sum
\everydisplay\expandafter{\the\everydisplay %% <- old \everydisplay
\renewcommand*\sum{\sum@beforelimitmodification\limits}% %% <- new addition
}
\makeatother %% <- revert @
Changing the limits for all operators:
I just thought of another completely different method that affects all big operators (compatible with \amsmath) at once.
With amsmath loaded, all big operators (apart from integrals) include \slimits@ in their definition, which simply expands to \displaylimits (which acts as \limits in \displaystyle and does nothing in other math styles).
By redefining it, you can give all operators used in display environments limits.
\documentclass{article}
\usepackage{amsmath}
\makeatletter %% <- make @ usable in command names
\renewcommand*\slimits@{\if@display\limits\else\displaylimits\fi}
\makeatother %% <- revert @
\begin{document}
Lorem $e^{\sum_{n=1}^\infty \frac1n}$ ipsum
\[
e^{\sum_{n=1}^\infty \frac1n}
\]
\begin{align}
e^{\sum_{n=1}^\infty \frac1n}&
\\
&e^{\sum_{n=1}^\infty \frac1n}
\end{align}
Lorem $e^{\sum_{n=1}^\infty \frac1n}$ ipsum
\end{document}
↑↑ Output looks identical, so see the image above ↑↑
If this doesn't work for some custom defined operator, say \myoperator, you should add \slimits@ to its definition, like this:
\makeatletter %% <- make @ usable in command names
\let\myoperator@beforelimitchange
\renewcommand*\myoperator{\DOTSB\myoperator@beforelimitchange\slimits@}
\makeatother %% <- revert @
 uses less horizontal space than this:
uses less horizontal space than this:
 But is in my opinion just as readable. The second case however will force me to put additional line-breaks or define further abbreviations.
But is in my opinion just as readable. The second case however will force me to put additional line-breaks or define further abbreviations.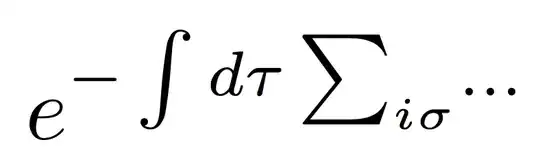


e^{...}us mathematically the same as\exp(...), so use the other form. – daleif Jan 27 '18 at 15:58\newcommand{\suml}{\sum\limits}, but the result is not at all pretty. It is not already without\limits. – egreg Jan 27 '18 at 16:13e^{.} \equiv \exp(.)however it is convention to usee^{.}. Mostly likely because it is denser and you need wait to many splits using\exp.\newcommand{\suml}{\sum\limits}was also what I thought of, but I thought there simply must be a more elegant and consistent way to do this in Latex. – DerWeh Jan 27 '18 at 18:06e^{...}cannot, a big minus in my book. The only time we've usede^exclusively was in some material for biologists as they are often not aware of the exp, they could also not understand the nolimit version of sum. I'd like to know the field you are working in. Where I work, it took me several years to get some "traditions" changed for things more readable to the end user. – daleif Jan 27 '18 at 22:16\hat{...}to mean something specific (like a conjugate in linear algebra). That was fine on an A, but almost invisible when applied to an actual 3x3 matrix (no use if widehat). I now thus this example when I explain to students (often from physics), that having these very short syntaxes are fine in some contexts, but utter rubbish in others, better to have two syntaxes for it. – daleif Jan 27 '18 at 22:22Mand then simply writee^M. This is just unreadable and unbalanced math line. It looks like something went wrong at the publisher at around the center of the line. Upright serifs with calligraphical letters with regular slanted variables. It's just a mismash. – percusse Jan 28 '18 at 16:45the missing possibility to manually break the exponent? – DerWeh Jan 28 '18 at 17:22expanddare required to be upright. – DerWeh Jan 28 '18 at 17:27