I have quadrilateral ABCD inscribed in a circle. I am to locate a point P on the line through C and D so that D is between it and C and
|DP| = (|AD|*|BC|)/|AB|.
The length of DP is drawn too long. What is wrong with the code that I have for locating P?
\documentclass{amsart}
\usepackage{tikz}
\usetikzlibrary{calc,intersections}
\begin{document}
\begin{tikzpicture}
\coordinate (O) at (0,0);
\draw[dashed] (195:2.5) arc (195:160:2.5);
\draw (160:2.5) arc (160:5:2.5);
\draw[dashed] (-15:2.5) arc (-15:5:2.5);
%Chord $\overline{AB}$ is drawn.
\path (100:2.5) coordinate (A) (160:2.5) coordinate (B) (5:2.5) coordinate (C) (40:2.5) coordinate (D);
\draw (A) -- (B) -- (C) -- (D) -- cycle;
\draw (A) -- (C);
\draw (B) -- (D);
%Labels for the endpoints of the chord AB are typeset.
\draw let \p1=($(A)-(B)$), \n1={atan(\y1/\x1)}, \p2=($(A)-(D)$), \n2={atan(\y2/\x2)} in node[anchor={0.5*(\n1+(\n2+180))+180}, inner sep=0] at ($(A) +({0.5*(\n1+(\n2+180))}:0.15)$){\textit{A}};
\draw let \p1=($(B)-(C)$), \n1={atan(\y1/\x1)} in node[anchor=\n1, inner sep=0] at ($(B) +({\n1+180}:0.15)$){\textit{B}};
\draw let \p1=($(B)-(C)$), \n1={atan(\y1/\x1)} in node[anchor={\n1+180}, inner sep=0] at ($(C) +(\n1:0.15)$){\textit{C}};
\draw let \p1=($(A)-(D)$), \n1={atan(\y1/\x1)}, \p2=($(C)-(D)$), \n2={atan(\y2/\x2)} in node[anchor={0.5*(\n1+(\n2+180))+180}, inner sep=0] at ($(D) +({0.5*(\n1+(\n2+180))}:0.15)$){\textit{D}};
%P is a point on the line through C and D so that D is between it and C, and |PD| = (|AD|*|BC|)/|AB|.
\path let \p1=($(A)-(B)$), \n1={veclen(\x1,\y1)}, \p2=($(A)-(D)$), \n2={veclen(\x2,\y2)}, \p3=($(B)-(C)$), \n3={veclen(\x3,\y3)} in coordinate (P) at
($(D)!{(-1*\n2*\n3/\n1)*1cm}!(C)$);
\draw[fill] (P) circle (1.5pt);
\draw[dashed] (P) -- (D);
\end{tikzpicture}
\end{document}
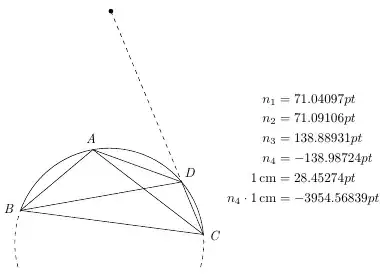


(D)you multiply with 1cm which is blowing up. The computations are in pt so you need 1pt. – percusse Mar 10 '18 at 21:13P. – user74973 Mar 10 '18 at 21:21cmwithpt? – user74973 Mar 10 '18 at 21:21($(D)!{-1*\n2*\n3/\n1}!(C)$). Edit: All the\nXare lengths inpt. – Torbjørn T. Mar 10 '18 at 22:492.5in the command\draw (160:2.5) arc (160:5:2.5)a measurement in points? – user74973 Mar 11 '18 at 17:21Plocated on the line throughCandDthat is at a distance fromDequal to(\n2*\n3)/\n1times the distance betweenCandD? – user74973 Mar 11 '18 at 17:22pt(1pt is about 0.3mm). In that case it'll be cm. For the second, you need to convert from pt to cm, so divide by 28.45 (https://tex.stackexchange.com/q/8260). – Torbjørn T. Mar 11 '18 at 17:40