How can make scope for rotating one disc around an axis?

Question

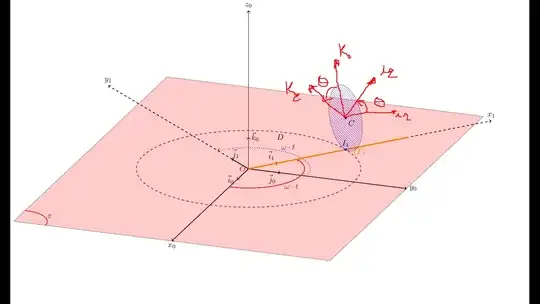
I have a rigid body formed by one disc (D) and one rod (T):

• I want to draw the rotation of the disc around the j_1 axis.

• I want the to make a scope for moving the disc on the stem and rotate it around the j_1 axis

If anyone can help me, here is my MWE:

\documentclass[border=0.5, tikz]{standalone}
\usepackage{tikz,tikz-3dplot}
\usepackage{ifthen}
\usetikzlibrary{patterns}% 
\begin{document}
\foreach \var in {0,10,...,180}{
\pgfmathsetmacro{\iAngle}{90}% change this value in degrees to show how 
the rod rotates around the z component
\tdplotsetmaincoords{70}{110}
\begin{tikzpicture}[scale=5,tdplot_main_coords]%A0
\useasboundingbox[tdplot_screen_coords] (-2.05,-1.2) rectangle 
(2.5,1.5);
\coordinate (O) at (0,0,0);
\coordinate (x0) at (2,0,0);
\coordinate (y0) at (0,1.5,0);
\node[red, left] at (O) {$O$};
\draw[thick,->] (O) -- (x0) node[anchor=north]{$x_0$};
\draw[thick,->] (O) -- (y0) node[anchor=west]{$y_0$};
\draw[thick,->] (O) -- (0,0,1.5) node[anchor=south]{$z_0$};
\draw[thick,->] (O) -- (0.3,0,0) node[anchor=north, left]{$\vec i_0$};
\draw[thick,->] (O) -- (0,0.3,0) node[near end, below]{$\vec j_0$};
\draw[thick,->] (O) -- (0,0,0.3) node[anchor=south, right]{$\vec 
k_0$};
\draw[thick, opacity=0.3] (-2,-1.5,0) -- (2,-1.5,0) -- (2,1.5,0) -- 
(-2,1.5,0) -- cycle;
\fill[red,opacity=0.2] (-2,-1.5,0) -- (2,-1.5,0) -- (2,1.5,0) -- 
(-2,1.5,0) -- cycle;
\tdplotdrawarc[thick, color=red]{(2,-1.5,0)}{-0.3}{-90}{0}{anchor=180}
{plan $P$}%
\tdplotdrawarc[thick, color=red, ->]{(O)}{0.5}{0}{\iAngle}{anchor=180, 
below}{$\omega\cdot t$}%
\tdplotdrawarc[thick,dotted, color=violet, ->]{(O)}{0.55}{90}
{90+\iAngle}{anchor=180,above}{$\omega\cdot t$}
\tdplotdrawarc[thick, color=purple, dashed]{(O)}{1}{0}{360}
{anchor=180}{}

\tdplotsetrotatedcoords{\iAngle}{0}{0}
\begin{scope}[tdplot_rotated_coords]%A1
\coordinate (x1) at (2,0,0);
\coordinate (y1) at (0,1.5,0);
\draw[thick, dashed, opacity=1, ->] (O) -- (x1)node[above] {$x_1$};
\draw[thick, dashed, opacity=1, ->] (O) -- (y1)node[above] {$y_1$};
\draw[thick,->] (O) -- (0.3,0,0) node[anchor=north, above left]{$\vec 
i_1$};
\draw[thick,->] (O) -- (0,0.3,0) node[near end, above]{$\vec j_1$};
\draw[ultra thick, color=orange, opacity=1] (O) -- (1,0,0)node[near end, below left] {$(T)$};
\coordinate[label=below right:$A1$] (A1) at (1,0,0.3);
\fill[blue,thick] (A1) circle (0.3pt);
\coordinate[label=above:$I_1$] (I1) at (1,0,0);
\fill[blue,thick] (I1) circle (0.3pt);
\end{scope}
\tdplotsetrotatedcoords{\var}{90}{0}
\begin{scope}[tdplot_rotated_coords]%A3
\node[above=1.52cm, left] at (A1){$(D)$};

 \ifthenelse{\var=180 \OR \var=0}{\draw[pattern=north west lines, 
pattern color=blue, opacity=0.5 ] (A1) circle (0.3);}
{\draw[pattern=bricks, pattern color=green, opacity=0.5 ] (A1) circle 
(0.3);}
\ifthenelse{\var=180 \OR \var=0}{\node[above=5.2cm, left=0.5cm] at 
(A1){\textbf{\textcolor{green}{in this disposition we can look the 
disk $(D)$ roll on the rod}}};}{\node[above=5.2cm, left=0.5cm] at (A1)
{\textbf{\textcolor{black}{I search the disposition of the disk $(D)$ 
where I can visualize its rotation on the rod around the $j_1$ 
component}}};}
\end{scope}

%%%%% I want to add this scope to show how the disk rolling on the rod 
(T), can you complete this part%%%

\tdplotsetrotatedcoords{\var}{90}{0}
\begin{scope}[tdplot_rotated_coords]%A3
\draw[-latex,blue] (A1) -- ++(-0.7,0,0)node[right]{$\vec k_1\equiv 
 \vec k_0$}; %<-
\draw[-latex,blue] (A1) -- ++(0,0,0.7)node[below]{$\vec i_1$};  %<-
\end{scope}

\tdplotsetrotatedcoords{\var}{45}{0} %90-45 angle
\begin{scope}[tdplot_rotated_coords]
\draw[-latex,blue] (A1) -- ++(-0.7,0,0)node[right]{$\vec k_2$}; %<-
\draw[-latex,blue] (A1) -- ++(0,0,0.7)node[below]{$\vec i_2$};  %<-

% Also, I want to show how the disk rotates around the $\vec j_1$ axis by $\theta$ angle in the plan formed by the $z_0Ox_1$.
\end{scope}
\end{tikzpicture}}
\end{document}

Update: This is an animated version of this code:

I want to add ($\vec i_1, \vec j_1, \vec k_1\equiv\vec k_0$) the coordinate system related to the disk, and the ($\vec i_2, \vec j_1, k_2$) the coordinate system related to its motion. If we compile this code we can look at page 12 of the .pdf and BOTH the coordinates systems are not in the plane of the disk. So, I want to add scope for those coordinates to show in the animated version of how the disk rolls on the rod illustrated in the figure with orange.

In order to complete this animation:

1. I want to add an iteration to show the backward motion of the disk on the rod

2. I don't have any idea how can I add the following commands: %\tdplotdrawarc[thick, color=blue,->]{(A1)}{0.5}{45}{90}{anchor=105, above, left}{$\theta$} % %\tdplotdrawarc[thick, color=red, ->]{(A1)}{0.5}{\iBngle}{180}{anchor=180, above}{$\theta$}%

3. As the rod coincides with the x1 axis, the reference systems attached to the disk $(\vec i_1, \vec k_0)$ should figure out the \vec k_0 parallel to the \overrightarrow{Oz_0} axis, and the \vec i_1 is parallel to the \overrightarrow{Ox_1} axis. The coordinate systems $(\vec i_2, \vec j_1, \vec k_2)$ showing how the disk moves backward and forward along the rod and it should coincide with the fixed axes Ox_1k_0 before the movement.

Here's my modification:

%%%%%%%%%%%  update  %%%%%%%%%%%%%%
\documentclass[border=5pt, tikz]{standalone}
\usepackage{tikz,tikz-3dplot}
\usepackage{animate}
\usepackage{ifthen}
\usetikzlibrary{patterns}% 
\def\relRad{0.3}
\def\RodLength{1.65}
\begin{document}
\tdplotsetmaincoords{70}{110}
%\begin{animateinline}[loop, poster = first, controls=false]{24}
\foreach \iBngle in {0,2,...,100}{
%\multiframe{100}{iBngle=0+2}{
\pgfmathsetmacro{\iAngle}{140}%35
\tdplotsetmaincoords{70}{110}
\begin{tikzpicture}[scale=5,tdplot_main_coords]
\useasboundingbox[tdplot_screen_coords] (-2.05,-1.2) rectangle 
(2.5,1.5);
\coordinate (O) at (0,0,0);
\node[red, left] at (O) {$O$};
\draw[thick,->] (O) -- (2,0,0) node[anchor=north]{$x_0$};
\draw[thick,->] (O) -- (0,1.5,0) node[anchor=west]{$y_0$};
\draw[thick,->] (O) -- (0,0,1.5) node[anchor=south]{$z_0$};
\draw[thick,->] (O) -- (0.3,0,0) node[anchor=north, left]{$\vec i_0$};
\draw[thick,->] (O) -- (0,0.3,0) node[near end, below]{$\vec j_0$};
\draw[thick,->] (O) -- (0,0,0.3) node[anchor=south, right]{$\vec 
k_0$};
\draw[thick, opacity=0.3] (-2,-1.5,0) -- (2,-1.5,0) -- (2,1.5,0) --(-2,1.5,0) -- cycle;
\fill[red,opacity=0.2](-2,-1.5,0) -- (2,-1.5,0) -- (2,1.5,0) --(-2,1.5,0) -- cycle;
\tdplotdrawarc[thick, color=red]{(2,-1.5,0)}{-0.3}{-90}{0}{anchor=180}
{$\pi/2$}% <-
\tdplotdrawarc[thick, color=red, ->]{(O)}{0.5}{0}{\iAngle+\iBngle}
{anchor=180, below}{$\omega\cdot t$}%
\tdplotdrawarc[thick,dotted, color=violet, ->]{(O)}{0.55}{90}
{90+\iAngle+\iBngle}{anchor=180,above}{$\omega\cdot t$}
\tdplotdrawarc[thick, color=purple, dashed]{(O)}
{\RodLength*\iBngle/180}{0}{360}{anchor=180}{} %%changed
\tdplotsetrotatedcoords{\iAngle+\iBngle}{00}{0}%%changed
\begin{scope}[tdplot_rotated_coords]
\draw[thick, dashed, opacity=1, ->] (0,0,0) -- (2.5,0,0)node[above]
{$x_1$};
\draw[thick, dashed, opacity=1, ->] (0,0,0) -- (0,2.5,0)node[above] 
{$y_1$};
\draw[thick,->] (O) -- (0.3,0,0) node[anchor=north, above left]{$\vec 
i_1$};
\draw[thick,->] (O) -- (0,0.3,0) node[near end, above]{$\vec j_1$};
\end{scope}
\tdplotsetrotatedcoords{{\iAngle+\iBngle}}{00}{0} %<- changed that in 
order to rotate the rod
\begin{scope}[tdplot_rotated_coords]
\draw[ultra thick, color=orange, opacity=1] (0,0,0) -- 
(\RodLength,0,0)node[near end, below left] {$(T)$};
\coordinate[label=below right:$C$] (A1) at 
({\RodLength*\iBngle/180},0,0.3); 
\fill[blue,thick] (A1) circle (0.3pt);
\coordinate[label=above:$I_1$] (I1) at 
({\RodLength*\iBngle/180},0,0);%changed
\fill[blue,thick] (I1) circle (0.3pt);
\end{scope}
\tdplotsetrotatedcoords{{\iAngle+130}}{90}{0} %<-
\begin{scope}[tdplot_rotated_coords]
\draw[pattern=north west lines, pattern color=blue, opacity=0.5 ] (A1) 
 circle (\relRad);
\node[] at (45:0.4cm){$D$};
\draw[-latex,blue] (A1) -- ++(0,0,0.7)node[below]{$k_1$};  %<-
\draw[-latex,blue] (A1) -- ++(0,0,0.7)node[below]{$i_1$};  %<-
\draw[-latex,blue] (A1) -- ++({-0.7*cos(\iBngle/\relRad+\iAngle)},0,{0.7*sin(\iBngle/\relRad+\iAngle)})node[right]{$i_2$}; %<-
\draw[-latex,blue] (A1) -- ++({-0.7*sin(\iBngle/\relRad)},0,{-0.7*cos(\iBngle/\relRad)})node[below]{$k_2$};  %<-
\end{scope}
\tdplotsetrotatedcoords{\iAngle}{90}{45}
\begin{scope}[tdplot_rotated_coords]
% \draw[-latex, violet] (A1) -- ++(-0.7,0,0)node[right]{$\vec k_2$};    

%\draw[-latex, violet] (A1) -- ++(0,0.7,0)node[right]{$\vec j_2$};
%\pgfmathtruncatemacro{\iBngle}{135} 
%\tdplotdrawarc[thick, color=blue,->]{(A1)}{0.5}{45}{90}{anchor=105, above, left}{$\theta$} %
%\tdplotdrawarc[thick, color=red, ->]{(A1)}{0.5}{\iBngle}{180}{anchor=180, above}{$\theta$}%
\end{scope}
\end{tikzpicture}
}
%\end{animateinline}
\end{document}

Answer 1

UPDATE: I am pretty sure that this is not yet what you want, but there seems to be a language barrier so we probably have to go in small steps. In this revision, the blue disk moves along the (orange) rod as it rotates.

\documentclass[border=5pt]{standalone}
\usepackage{tikz,tikz-3dplot}
\usepackage{animate}
\usepackage{ifthen}
\usetikzlibrary{patterns}% 
\def\relRad{0.3}
\def\RodLength{1.65}
\begin{document}
\tdplotsetmaincoords{70}{110}
\begin{animateinline}[loop, poster = first, controls=false]{24}
\multiframe{30}{iBngle=0+6}{
\pgfmathsetmacro{\iAngle}{140}%35
\tdplotsetmaincoords{70}{110}
\begin{tikzpicture}[scale=5,tdplot_main_coords]
\useasboundingbox[tdplot_screen_coords] (-2.05,-1.2) rectangle (2.5,1.5);
\coordinate (O) at (0,0,0);
\node[red, left] at (O) {$O$};
\draw[thick,->] (O) -- (2,0,0) node[anchor=north]{$x_0$};
\draw[thick,->] (O) -- (0,1.5,0) node[anchor=west]{$y_0$};
\draw[thick,->] (O) -- (0,0,1.5) node[anchor=south]{$z_0$};
\draw[thick,->] (O) -- (0.3,0,0) node[anchor=north, left]{$\vec i_0$};
\draw[thick,->] (O) -- (0,0.3,0) node[near end, below]{$\vec j_0$};
\draw[thick,->] (O) -- (0,0,0.3) node[anchor=south, right]{$\vec k_0$};
\draw[thick, opacity=0.3] (-2,-1.5,0) -- (2,-1.5,0) -- (2,1.5,0) -- (-2,1.5,0) -- cycle;
\fill[red,opacity=0.2]
(-2,-1.5,0) -- (2,-1.5,0) -- (2,1.5,0) -- (-2,1.5,0) -- cycle;
\tdplotdrawarc[thick, color=red]{(2,-1.5,0)}{-0.3}{-90}{0}{anchor=180}
{$\pi/2$}% <-
\tdplotdrawarc[thick, color=red, ->]{(O)}{0.5}{0}{\iAngle}{anchor=180, 
 below}{$\omega\cdot t$}%
\tdplotdrawarc[thick,dotted, color=violet, ->]{(O)}{0.55}{90}{90+\iAngle}{anchor=180,above}{$\omega\cdot t$}
\tdplotdrawarc[thick, color=purple, dashed]{(O)}{\iBngle/180}{0}{360}{anchor=180}{} 
\tdplotsetrotatedcoords{\iAngle}{00}{0}
\begin{scope}[tdplot_rotated_coords]
\draw[thick, dashed, opacity=1, ->] (0,0,0) -- (2.5,0,0)node[above] {$x_1$};
\draw[thick, dashed, opacity=1, ->] (0,0,0) -- (0,2.5,0)node[above] {$y_1$};
\draw[thick,->] (O) -- (0.3,0,0) node[anchor=north, above left]{$\vec i_1$};
\draw[thick,->] (O) -- (0,0.3,0) node[near end, above]{$\vec j_1$};
\end{scope}
\tdplotsetrotatedcoords{{\iAngle+\iBngle}}{00}{0} %<- changed that in order to rotate the rod
\begin{scope}[tdplot_rotated_coords]
\draw[ultra thick, color=orange, opacity=1] (0,0,0) -- (\RodLength,0,0)node[near end, below left] {$(T)$};
\coordinate[label=below right:$C$] (A1) at ({\RodLength*\iBngle/180},0,0.3); 
\fill[blue,thick] (A1) circle (0.3pt);
\coordinate[label=above:$I_1$] (I1) at (1,0,0);
\fill[blue,thick] (I1) circle (0.3pt);
\end{scope}
\tdplotsetrotatedcoords{{\iAngle+130}}{90}{0} %<-
\begin{scope}[tdplot_rotated_coords]
\draw[pattern=north west lines, pattern color=blue, opacity=0.5 ] (A1) circle
(\relRad);
\node[] at (45:0.4cm){$D$};
\draw[-latex,blue] (A1) -- ++({-0.7*cos(\iBngle/\relRad)},{0.7*sin(\iBngle/\relRad)},0)node[right]{$k_0$}; %<-
\draw[-latex,blue] (A1) -- ++(0,0,0.7)node[below]{$k_1$};  %<-
\draw[-latex,blue] (A1) -- ++({-0.7*sin(\iBngle/\relRad)},{-0.7*cos(\iBngle/\relRad)},0)node[below]{$k_2$};  %<-
\end{scope}
\tdplotsetrotatedcoords{\iAngle}{90}{45}
\begin{scope}[tdplot_rotated_coords]
% \draw[-latex, violet] (A1) -- ++(-0.7,0,0)node[right]{$\vec k_2$};    
%\draw[-latex, violet] (A1) -- ++(0,0.7,0)node[right]{$\vec j_2$};
%\pgfmathtruncatemacro{\iBngle}{135} 
%\tdplotdrawarc[thick, color=blue,->]{(A1)}{0.5}{45}{90}{anchor=105, above, left}{$\theta$} %
%\tdplotdrawarc[thick, color=red, ->]{(A1)}{0.5}{\iBngle}{180}{anchor=180, above}{$\theta$}%
\end{scope}
\end{tikzpicture}
}
\end{animateinline}

OLD(ER) ANSWER: This code looks somehow familiar... (It might be appropriate to give links to all sources.) To give you a start:

\documentclass[border=5pt]{standalone}
\usepackage{tikz,tikz-3dplot}
\usepackage{animate}
\usepackage{ifthen}
\usetikzlibrary{patterns}% 
% \newcounter{MyCounter}
% \def\StartValue{5}
% \def\MaxValue{10}
\def\relRad{0.3}
\begin{document}
\tdplotsetmaincoords{70}{110}
\begin{animateinline}[loop, poster = first, controls]{24}
  \multiframe{30}{iBngle=0+3}{
\pgfmathsetmacro{\iAngle}{140}%35
\tdplotsetmaincoords{70}{110}
\begin{tikzpicture}[scale=5,tdplot_main_coords]
\useasboundingbox[tdplot_screen_coords] (-2.05,-1.2) rectangle (2.5,1.5);
\coordinate (O) at (0,0,0);
\node[red, left] at (O) {$O$};
\draw[thick,->] (O) -- (2,0,0) node[anchor=north]{$x_0$};
\draw[thick,->] (O) -- (0,1.5,0) node[anchor=west]{$y_0$};
\draw[thick,->] (O) -- (0,0,1.5) node[anchor=south]{$z_0$};
\draw[thick,->] (O) -- (0.3,0,0) node[anchor=north, left]{$\vec i_0$};
\draw[thick,->] (O) -- (0,0.3,0) node[near end, below]{$\vec j_0$};
\draw[thick,->] (O) -- (0,0,0.3) node[anchor=south, right]{$\vec k_0$};
\draw[thick, opacity=0.3] (-2,-1.5,0) -- (2,-1.5,0) -- (2,1.5,0) -- (-2,1.5,0) -- cycle;
\fill[red,opacity=0.2]
(-2,-1.5,0) -- (2,-1.5,0) -- (2,1.5,0) -- (-2,1.5,0) -- cycle;
\tdplotdrawarc[thick, color=red]{(2,-1.5,0)}{-0.3}{-90}{0}{anchor=180}
{$\pi/2$}% <-
\tdplotdrawarc[thick, color=red, ->]{(O)}{0.5}{0}{\iAngle}{anchor=180, 
 below}{$\omega\cdot t$}%
\tdplotdrawarc[thick,dotted, color=violet, ->]{(O)}{0.55}{90}{90+\iAngle}{anchor=180,above}{$\omega\cdot t$}
\tdplotdrawarc[thick, color=purple, dashed]{(O)}{1}{0}{360}{anchor=180}{} 
\tdplotsetrotatedcoords{\iAngle}{00}{0}
\begin{scope}[tdplot_rotated_coords]
\draw[thick, dashed, opacity=1, ->] (0,0,0) -- (2.5,0,0)node[above] {$x_1$};
\draw[thick, dashed, opacity=1, ->] (0,0,0) -- (0,2.5,0)node[above] {$y_1$};
\draw[thick,->] (O) -- (0.3,0,0) node[anchor=north, above left]{$\vec i_1$};
\draw[thick,->] (O) -- (0,0.3,0) node[near end, above]{$\vec j_1$};
\end{scope}
\tdplotsetrotatedcoords{{\iAngle+\iBngle}}{00}{0} %<- changed that in order to rotate the rod
\begin{scope}[tdplot_rotated_coords]
\draw[ultra thick, color=orange, opacity=1] (0,0,0) -- (1.65,0,0)node[near end, below left] {$(T)$};
\coordinate[label=below right:$C$] (A1) at (1,0,0.3); 
\fill[blue,thick] (A1) circle (0.3pt);
\coordinate[label=above:$I_1$] (I1) at (1,0,0);
\fill[blue,thick] (I1) circle (0.3pt);
\end{scope}
\tdplotsetrotatedcoords{{\iAngle+\iBngle}}{90}{0} %<-
\begin{scope}[tdplot_rotated_coords]
\draw[pattern=north west lines, pattern color=blue, opacity=0.5 ] (A1) circle
(\relRad);
\node[] at (45:0.4cm){$D$};
\draw[-latex,blue] (A1) -- ++({-0.7*cos(\iBngle/\relRad)},{0.7*sin(\iBngle/\relRad)},0)node[right]{$k_0$}; %<-
\draw[-latex,blue] (A1) -- ++(0,0,0.7)node[below]{$k_1$};  %<-
\draw[-latex,blue] (A1) -- ++({-0.7*sin(\iBngle/\relRad)},{-0.7*cos(\iBngle/\relRad)},0)node[below]{$k_2$};  %<-
\end{scope}
\tdplotsetrotatedcoords{\iAngle}{90}{45}
\begin{scope}[tdplot_rotated_coords]
% \draw[-latex, violet] (A1) -- ++(-0.7,0,0)node[right]{$\vec k_2$};    
%\draw[-latex, violet] (A1) -- ++(0,0.7,0)node[right]{$\vec j_2$};
%\pgfmathtruncatemacro{\iBngle}{135} 
%\tdplotdrawarc[thick, color=blue,->]{(A1)}{0.5}{45}{90}{anchor=105, above, left}{$\theta$} %
%\tdplotdrawarc[thick, color=red, ->]{(A1)}{0.5}{\iBngle}{180}{anchor=180, above}{$\theta$}%
\end{scope}
\end{tikzpicture}
}
\end{animateinline}
\end{document}

I hope that's closer to what you want. BTW, the angle labeled \pi in the front left corner is just \pi/2.

NOTICE: The code produces an inline animation. It can be converted to an animated gif by using this cool post. (Note also that this post which works for beamer animations.)