Division of curved edges in tikz

Question

I need to divide an edge into a number of equal parts. I have the following way to do this for straight edges:

    \begin{tikzpicture}
       [very thick, transform shape, scale=.2,
       rect/.style={rectangle,  }
       ]

       \node[rect, fill = red,minimum width =.005cm, minimum height = 1cm] (1) at (20,0) {};
       \node[rect, fill = red,minimum width =.005cm, minimum height = 1cm] (2) at (0,0) {};
       \node[rect,  fill = red, minimum width =.005cm, minimum height = 1cm ](3) at (5,0) {};
       \node[rect, fill = red, minimum width =.005cm, minimum height = 1cm ](4) at (10,0) {};
       \node[rect,  fill = red, minimum width =.005cm, minimum height = 1cm ](5) at (15,0) {};
       \path[-]

       (1) edge[bend left = 0, red] node {} (2)
       ;

    \end{tikzpicture}

Which results in this:

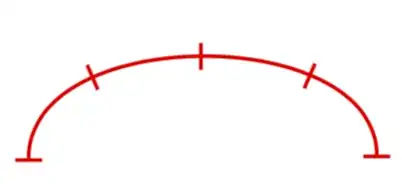
I want to do a similar thing for an edge that is curved. My issue is that I can't think of an easy way to find the coordinates of equal line segments of a curved edge, and then rotate each node so that it is perpendicular to the edge.

I was hoping to find a way where it is not necessary to define the coordinates of the edge dividers, or the rotation of the dividers, is this possible?

If not does anyone know where I can find information on the Bezier curves used in tikz as I can try to code a program to calculate the locations and slope of the curve at those points.

This is how I usually define curved edges fyi:

    \begin{tikzpicture}
       [very thick, transform shape, scale=.2,
       rect/.style={rectangle,  }
       ]
       \node[rect, rotate=90,fill = red,minimum width =.005cm, minimum height = 1cm] (1) at (20,0) {};
       \node[rect, rotate=90, fill = red,minimum width =.005cm, minimum height = 1cm] (2) at (0,0) {};
       \node[rect,  fill = red, minimum width =.005cm, minimum height = 1cm ](3) at (5,0) {};
       \node[rect, fill = red, minimum width =.005cm, minimum height = 1cm ](4) at (10,0) {};
       \node[rect,  fill = red, minimum width =.005cm, minimum height = 1cm ](5) at (15,0) {};
       \path[-]

       (1) edge[bend left = -90, red] node {} (2)
       ;

\end{tikzpicture}

Which gives:

Answer 1

You can use a decoration. The main problem is the mark at the end of path (see Tikz: decoration at path end disappears at high bend angles).

\documentclass[tikz,border=2mm]{standalone} 
\usetikzlibrary{positioning, decorations.markings}

\begin{document}
   \begin{tikzpicture}
       [very thick, 
       decoration={markings,
        mark=between positions 0 and 1 step .25 with {\node[inner xsep=1pt, fill=black, transform shape]{};}}
       ]
       \draw[postaction={decorate}] (0,0) to[out=90, in=90] (4,0) node[inner xsep=1pt, fill=black, rotate=90]{};
\end{tikzpicture}
\end{document}

Answer 2

Very similar to @Ignasi's answer, the main difference being that I use bar arrows to draw the bars. This allows one to avoid having to rotate the disappearing mark by hand.

\documentclass[tikz,border=3.14mm]{standalone} 
\usetikzlibrary{decorations.markings}

\begin{document}
\begin{tikzpicture}
       \draw[red,very thick,-Bar,postaction={decorate},
       decoration={markings,
        mark=between positions 0 and 1 step .25 with {
        \arrow{Bar};}}] (0,0) to[out=90, in=90] (4,0);
\end{tikzpicture}
\end{document}