3

I am wondering if one can install 3D spherical coordinates in pgfplots (not TikZ). Questions of this sort have been already asked, but as far as I can see, the answers here, here, here and here all write the conversion in the arguments, so they do something along the lines of 

\addplot3[...] ({cos(x)*cos(y)},{cos(x)*sin(y)},{1 + 0.2*sin(x)*sin(y)});

In this question, I am asking for something different. In plain TikZ one may switch to spherical coordinates, as illustrated in the MWE

\documentclass{article}
\pagestyle{empty}
\usepackage{tikz}
\usetikzlibrary{3d}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}

\makeatletter
\newcommand{\SwitchToPolar}{% based on https://tex.stackexchange.com/a/365418/121799
\def\tikz@parse@splitxyz##1##2##3,##4,{%
    \def\@next{\tikz@scan@one@point##1(xyz spherical cs:angle=##2,radius=##3,latitude=##4 r)}%
}}
\newcommand{\SwitchToNormal}{%
\def\tikz@parse@splitxyz##1##2##3,##4,{%
  \def\@next{##1{\pgfpointxyz{##2}{##3}{##4}}}%
}}  
\makeatother
\begin{document}

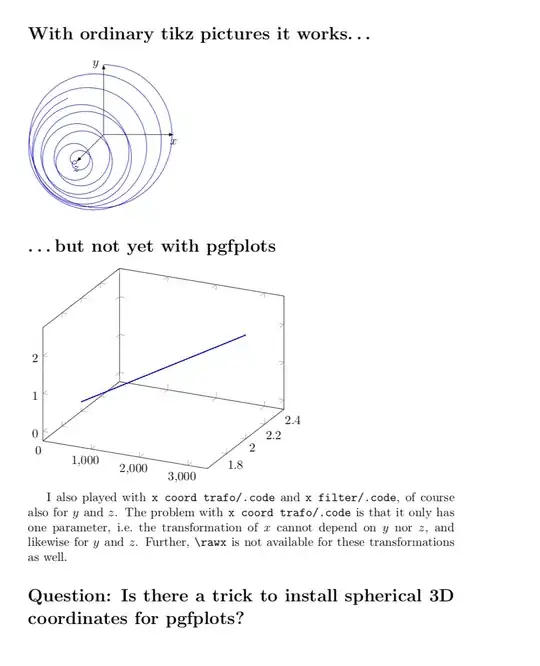
\section*{With ordinary tikz pictures it works\dots}

\begin{tikzpicture}
 \draw[-latex] (0,0,0) -- (2,0,0) node[below]{$x$};
 \draw[-latex] (0,0,0) -- (0,2,0) node[left]{$y$};
 \draw[-latex] (0,0,0) -- (0,0,2) node[below]{$z$};
 \SwitchToPolar
 \draw[blue] plot[variable=\x,domain=0:200,samples=200,smooth] 
 ({17*\x},2,{\x/80});
 \SwitchToNormal
\end{tikzpicture}

\section*{\dots but not yet with pgfplots}

\begin{tikzpicture}
%\SwitchToPolar
\begin{axis}
\SwitchToPolar
\addplot3[blue,domain=0:200,samples=20,
%execute at begin plot={\SwitchToPolar}
] ({17*x},2,{x/80});
\end{axis}
\end{tikzpicture}

I also played with \texttt{x coord trafo/.code} and 
\texttt{x filter/.code}, of course also for $y$ and $z$. The problem with 
\texttt{x coord trafo/.code} is that it only has one parameter, i.e.\ the
transformation of $x$ cannot depend on $y$ nor $z$, and likewise for $y$ and
$z$. Further, \verb|\rawx| is not available for these transformations as well.

\section*{Question: Is there a trick to install spherical 3D coordinates for pgfplots?}

\end{document}

enter image description here

As you can see, the coordinate change has been ignored. Is there any way to make it work? (In the MWE I list things that I have tried but that do not work.)

What would that be potentially good for? I guess it would just make some things simpler. After all, pgfplots does have 2D polar coordinates.

  • I should also have mentioned that something like (xyz spherical cs:...) doesn't seem to work either. –  Jul 03 '18 at 00:28
  • I think you would need to set up a suitable coordinate system for pgfplots and not try to switch to a non-pgfplots system in the pgfplots context i.e. you're proceeding as if pgfplots uses TikZ coordinate systems, but that's not true, is it? – cfr Jul 03 '18 at 00:55
  • @cfr That is most likely true but I do not know how to set up the coordinate system for pgfplots. I just thought I could trick pgfplots, but obviously that did not work. (My main motivation is to avoid reinventing the plot handler that pgfplot has, but things are much more tricky than I thought. Somehow pgfplots manages to add some meta information which allows one to change the color along the path, which is actually nontrivial to do in TikZ. But perhaps I need to go along another path ;-) Anyway, the question is just to check if anyone did that already. –  Jul 03 '18 at 01:01

0 Answers0