Why tikz fail at computation?

Question

I'am using tikz for helping me at work. I want to produce a results sheet for an exam in which each students have different numerical results (there is a free parameter that is the alphabetical position of each student). Usually it work, but sometimes tikz fail to evaluate some of the results. Usually when there are big numbers. I have the following message

! Dimension too large. \pgfmath@x l.97 } I can't work with sizes bigger than about 19 feet. Continue and I'll use the largest value I can.

This came from the following code

\documentclass{article}
\usepackage{tikz}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{1pt}%
\begin{document}
\begin{tikzpicture}
\pgfmathsetseed{5511}
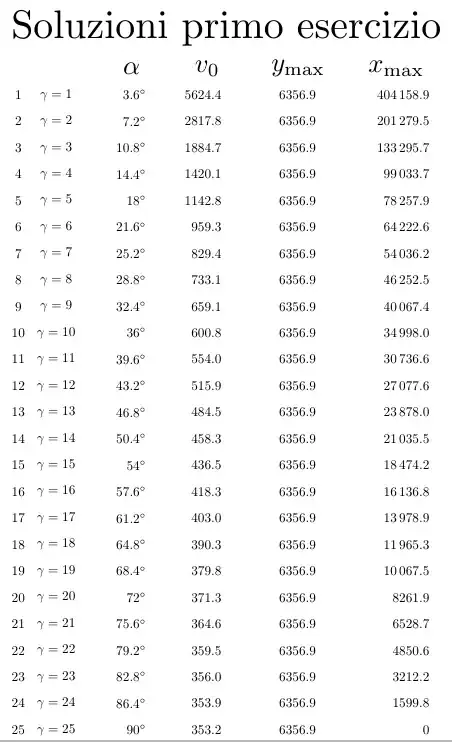
\node[scale=3]at(6,26){Soluzioni primo esercizio};
\node[scale=2]at(6,25){$\alpha$};
\node[scale=2]at(8,25){$v_0$};
\node[scale=2]at(10,25){$y_{max}$};
\node[scale=2]at(12,25){$x_{max}$};
\foreach \k/\nome in {1...25}
{
\pgfmathsetmacro{\y}{(25-\k)}
\node[]at(0,\y){\nome};
\node[]at(2,\y){$\gamma=\k$};
\pgfmathsetmacro{\g}{9.81}
\pgfmathsetmacro{\tvolo}{72}
\pgfmathsetmacro{\angolo}{18*\k/5}
\pgfmathsetmacro{\vzero}{\tvolo*\g/(2*sin(\angolo))}
\pgfmathsetmacro{\seno}{sin(\angolo)}
\pgfmathsetmacro{\ymax}{\vzero*\vzero*sin(\angolo)*sin(\angolo)/(2*\g)}
\pgfmathsetmacro{\xmax}{\vzero*\vzero*sin(2*\angolo)/\g}
\node[]at(6,\y){$\angolo^\circ$};
\node[]at(8,\y){$\vzero$};
\node[]at(10,\y){$\ymax$};
\node[]at(12,\y){$\xmax$};
}
\end{tikzpicture}
\end{document}

Tikz fail to calculate y_max (max altitude) and x_max (horizontal displacement), in particular when k=1 one must find

• angle = 3.5999°
• initial velocity = 5624.58 m/s
• y_max = 6356 m
• x_max = 404209 m

instead tikz cannot reproduce the correct results. Why?

Answer 1

The numerical capabilities of pgf are limited, you probably exceeded the limit. The xfp package, and its \fpeval, can however handle larger numbers. A quite simple implementation is found below. I also used siunitx to print the values, and changed the coordinates of the nodes a bit.

\documentclass{standalone}
\usepackage{tikz}
\usepackage{xfp} % for fpeval
\usepackage{siunitx} % for \num, number printing

\begin{document}
\begin{tikzpicture}[y=0.7cm]
\sisetup{
  round-mode=places,
  round-precision=1
}
\pgfmathsetseed{5511}
\node[scale=3]at(5.5,26.5){Soluzioni primo esercizio};
\node[scale=2]at(3,25){$\alpha$};
\node[scale=2]at(5,25){$v_0$};
\node[scale=2]at(7.4,25){$y_{\max}$};
\node[scale=2]at(10,25){$x_{\max}$};
\foreach \k/\nome in {1,...,25}
{
  \pgfmathsetmacro{\y}{(25-\k)}
  \node at (0,\y){\nome};
  \node at (1,\y){$\gamma=\k$};
  \pgfmathsetmacro{\g}{9.81}
  \pgfmathsetmacro{\tvolo}{72}
  \edef\angolo{\fpeval{18*\k/5}}
  \edef\vzero{\fpeval{\tvolo*\g/(2*sind(\angolo))}}
  \edef\seno{\fpeval{sind(\angolo)}}
  \edef\ymax{\fpeval{\vzero*\vzero*sind(\angolo)*sind(\angolo)/(2*\g)}}
  \edef\xmax{\fpeval{\vzero*\vzero*sind(2*\angolo)/\g}}
  \node [left] at (3.5,\y) {$\SI{\angolo}{\degree}$};
  \node [left] at (5.5,\y) {$\num{\vzero}$};
  \node [left] at (8,\y)   {$\num{\ymax}$};
  \node [left] at (11,\y)  {$\num{\xmax}$};
}
\end{tikzpicture}
\end{document}