Producing a triangle diagram with sections

Question

Hi, I am fairly new to LaTeX. I am trying to create the equilateral triangle shown in this sketch, I have provided the code for what I have so far but am stuck at this stage, is there a simpler way? Is this the best package to use? If so what is the next step?

\documentclass[a4paper,12pt]{article}
\usepackage{tikz}
\begin{document}

\begin{tikzpicture}
\draw (0,0) node[anchor=north]{$A$}
  -- (4,0) node[anchor=north]{$B$}
  -- (2,4) node[anchor=south]{$C$}
   -- cycle;
\end{tikzpicture}
\end{document}

Answer 1

You can use \foreach loops and polar coordinates for this.

The first \foreach is

\foreach \angle/\label in {90/C,210/A,330/B}{
    \coordinate[label={\angle:\label}] (\label) at (\angle:2){};
}

Which is equivalent to

\coordinate[label={210:A}] (A) at ({2*cos(210)},{2*sin(210)});
\coordinate[label={330:B}] (B) at ({2*cos(330)},{2*sin(330)});
\coordinate[label={ 90:C}] (C) at ({2*cos( 90)},{2*sin( 90)});

Notice that the polar coordinates are equal to expressing the x as radius*cos(angle) and the y as radius*sin(angle). I often find this notation easier.

The second \foreach is

\foreach [count=\i] \angle in {240,180,...,-60}{
    \node at (\angle:0.75){\i};
}

Which is already saving us quite some work, because it is equivalent to

\node at ({0.75*cos(240)},{0.75*sin(240)}){1};
\node at ({0.75*cos(180)},{0.75*sin(180)}){2};
\node at ({0.75*cos(120)},{0.75*sin(120)}){3};
\node at ({0.75*cos( 60)},{0.75*sin( 60)}){4};
\node at ({0.75*cos(  0)},{0.75*sin(  0)}){5};
\node at ({0.75*cos(-60)},{0.75*sin(-60)}){6};

Which is just cumbersome to type in manually.

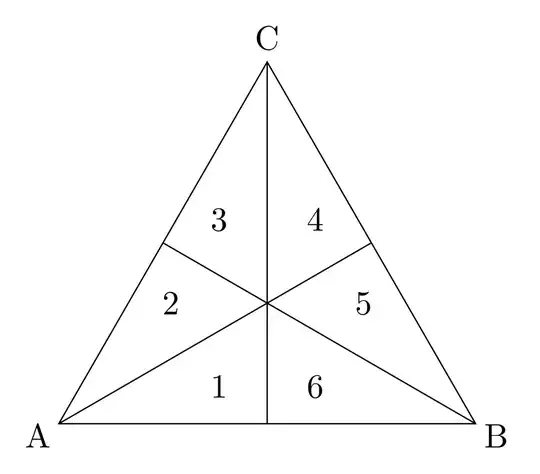
The command \draw (A) -- coordinate (AB) (B) -- coordinate (BC) (C) -- coordinate (CA) cycle; is used to draw the edges of the triangle, and at the same time defines the coordinates (AB), (BC) and (CA) that lie between the corners.

The last thing remaining is to draw the lines from the middle of the edges to the opposite corners, which is done with

\draw (A) -- (BC);
\draw (B) -- (CA);
\draw (C) -- (AB);

Because we already defined the coordinates while drawing the edges.

If you want to use mathematical expressions inside the coordinate definitions (e.g. sin(90)), you have to enclose the expression in braces, because Tikz will get confused at the parentheses inside the expression.

The complete code is:

\documentclass[tikz]{standalone}

\begin{document}
    \begin{tikzpicture}
        \foreach \angle/\label in {90/C,210/A,330/B}{
            \node[coordinate,label={\angle:\label}] (\label) at (\angle:2){};
        }
        \draw (A) -- coordinate (AB) (B) -- coordinate (BC) (C) -- coordinate (CA) cycle;

        \draw (A) -- (BC);
        \draw (B) -- (CA);
        \draw (C) -- (AB);

        \foreach [count=\i] \angle in {240,180,...,-60}{
            \node at (\angle:0.75){\i};
        }
    \end{tikzpicture}
\end{document}

The fact that the triangle is a equilateral directly follows from using polar coordinates with the same radius and the same angle difference.

Answer 2

Really just for fun. EDIT: Simplified the evaluation of \Z and removed the overshooting of the segment lines, very big thanks to @MaxSnippe, and moved the alphabetic labels a bit closer to the corners.

\documentclass[tikz,border=3.14mm]{standalone}
\usetikzlibrary{shapes.geometric,calc}
\newcounter{cheat}
\begin{document}
\begin{tikzpicture}
\node[minimum size=5cm,regular polygon,draw,regular polygon sides=3,outer
sep=0pt] (a) {};
\foreach \X [evaluate=\X as \Y using {int(1+mod(\X,3))},
evaluate=\X as \Z using {int(1+mod(1+\X,3))}] in {1,2,3}
{\draw ($(a.corner \X)!0.5!(a.corner \Y)$) -- (a.corner \Z);
\setcounter{cheat}{\Z}
\node at ($1.1*(a.corner \X)$) {\Alph{cheat}};
}
\foreach \X[count=\Y] in {240,180,...,-60}
{\node at (\X:1) {\Y};}
\end{tikzpicture}
\end{document}

Answer 3

Here's a version in Metapost + luamplib. Compile with lualatex.

\documentclass[border=5mm]{standalone}
\usepackage{luatex85}
\usepackage{luamplib}
\begin{document}
\mplibtextextlabel{enable}
\begin{mplibcode}
beginfig(1);
path T;
T = for t=7 step 4 until 15: 72 dir 30t -- endfor cycle;
for i=0 upto 2:
  draw point i of T -- point 3/2 + i of T withcolor 1/2 white;
  label("$" & char (65+i) & "$", 9/8 point i of T);
endfor
for i=1 upto 6: 
  label("$" & decimal i & "$", 2/3 point 1/3 (2 - 2i + ceiling 1/2i) of T);
endfor
draw T;
endfig;
\end{mplibcode}
\end{document}