In this question we use a lot of possibilities to define a cube. One idea is to name the vertices. I would like to find something to create these names automatically. In my last example in the question, I used nodes named 000,010,...,111. Now I would like to transform these names (or references, I don't know what is the exact term in english) in the conventional names A,B,...,H. To make this I use three loops to get 8 numbers in binary representation.
I convert these numbers to base 10. Logically the formula is 1+\x+2*\y+4*\z but I wanted to
invert two names because I would get A,B,C,D and not A,B,D,C so I use a little trick :
1+\x+2*\y+4*\z+\y*(\y-2*\x).
With a counter cnt and the macro \Alph no problem but now (it's my quesion) I would like to avoid the use of a counter and to replace \Alph by \@Alph but something goes wrong.
This little code works
\makeatletter
\def\tmp{10}
\def\macro{\@Alph{\tmp}}
\macro
\begin{tikzpicture}
\node(\macro){\macro};
\draw (J)--++(5,1);
\end{tikzpicture}
My main code works also
\documentclass{scrartcl}
\usepackage{tikz}
\begin{document}
\newcounter{cnt}
\begin{tikzpicture}[ x={(-0.5cm,-0.5cm)}, y={(1cm,0cm)}, z={(0cm,1cm)},
every node/.style={shape=circle,draw}]
\foreach \z in {0,1}
\foreach \y in {0,1}
\foreach \x in {0,1}
{\pgfmathtruncatemacro{\nb}{1+\x+2*\y+4*\z+\y*(\y-2*\x)}
\setcounter{cnt} {\nb}
\node (\Alph{cnt}) at (4*\x,4*\y,4*\z) {\Alph{cnt}};
}%
\end{tikzpicture}
\end{document}
I would like to write something like that
Wrong code
\documentclass{scrartcl}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}[x={(-0.5cm,-0.5cm)}, y={(1cm,0cm)}, z={(0cm,1cm)},
every node/.style={shape=circle,draw}]
\foreach \z in {0,1}
\foreach \y in {0,1}
\foreach \x in {0,1}
{\pgfmathtruncatemacro{\nb}{1+\x+2*\y+4*\z+\y*(\y-2*\x)}
\makeatletter
\def\name{\@Alph{\nb}}
\node (\name) at (4*\x,4*\y,4*\z) {\name};
} %
\end{tikzpicture}
\end{document}
But I get a lot of insults and particularly:
Missing \endcsname inserted.
<to be read again>
\spacefactor
Where is my mistake ?
The result is a future cube :
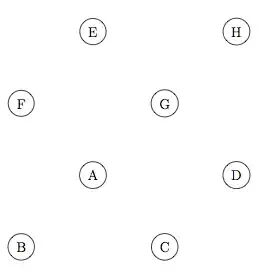
\nbdefined? – egreg Feb 21 '12 at 20:31\nbis first a number between 0 and 7 with\x+2*\y+4*\z, the normal representation base 10. I get 000, 100, 010, 110, 001, 101, 011, 111, to get 000, 100, 110, 010, 001, 101, 111, 011 I added \y(\y-2\x) and finally to get a number between 1 and 8 I added 1. Voilà ! – Alain Matthes Feb 21 '12 at 22:11