I'm afraid your problem can't be solved (at least in legacy TeX implementations, maybe LuaTeX can do something about it).
A relation symbol (defined with \mathchardef and given class 3), a simple character (given class 3 through its \mathcode), a symbol in a different class but preceded by \mathrel or finally a subformula in the reach of \mathrel (that is, \mathrel{<subformula>}), are marked as relation nodes in the math list that's being built.
When the formula ends, the math list is traversed from left to right and TeX builds boxes from nodes, also inserting spaces and penalties when needed.
For instance it will insert no space and no penalty between consecutive relation nodes, but a thick space between a different class node and a relation node according to the table

(see https://tex.stackexchange.com/a/81777/4427 for details).
Thus, if you do x\in\pref(A), there will be no space between \in and \pref and no space between \pref and (. But, as there's no “looking back”. There is just one “impossible” case in the 3 row and in the 3 column, that is, Rel-Bin or Bin-Rel, in which case the Bin node is made into an Ord one. The Rel nodes never change their class.
The “impossible cases” in the table are what makes binary operation nodes (class 2) become Ord nodes (so unary operators) in certain cases.
One would be tempted to use Bin nodes and change the size of \medmuskip to match \thickmuskip with something like
\newmuskip\savemedmuskip
\newcommand{\pref}{%
\savemedmuskip=\medmuskip
\medmuskip=\thickmuskip
\mathbin R
\medmuskip=\savemedmuskip
}
which was the (amended) proposal by Steven B. Segletes will not work, because TeX uses a single value for \medmuskip, precisely the one holding when the formula ends.
Steven's trick seems to work in an example, but just because his macro happens to do \medmuskip=\medmuskip instead of restoring a saved value.
Let's try
\documentclass{article}
\usepackage{amsmath}
\newmuskip\savemedmuskip
\newcommand{\pref}{%
\savemedmuskip=\medmuskip
\medmuskip=\thickmuskip
\mathbin R
\medmuskip=\savemedmuskip
}
\begin{document}
$a \mathrel R b$
$a \mathbin R b$
$a \pref b$
\end{document}
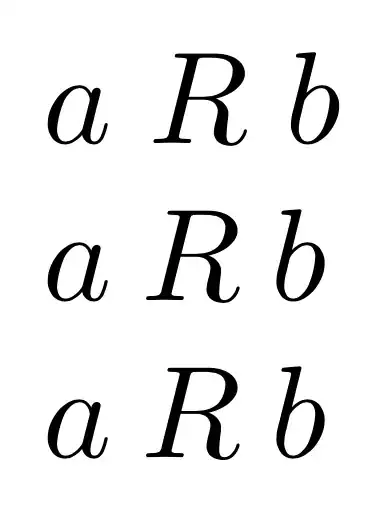
As you see, the second and third formulas are exactly the same.
If you want to change a Rel object into an Ord one, the only way is to brace it.
You could avoid braces by defining a *-variant:
\makeatletter
\newcommand{\pref}{\@ifstar{R}{\mathrel R}}
\makeatother
Example:
\documentclass{article}
\usepackage{amsmath}
\makeatletter
\newcommand{\pref}{\@ifstar{R}{\mathrel R}}
\makeatother
\begin{document}
$a \pref b$
$a \in \pref*(A)$
\end{document}


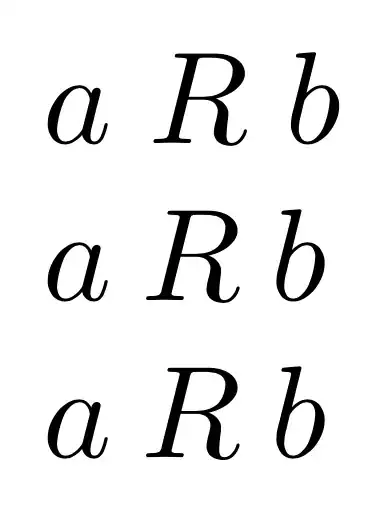

{\pref}would do – egreg Oct 24 '18 at 16:10{\pref}or how it adjusts according to context? (I like to know how I am supposed to use the commands rather than find it out by trial and error, which becomes impractical when many combinations are possible, and I couldn’t find this explained in ams doc or Lamport’s book.) – Olivier Cailloux Oct 24 '18 at 18:36{<math material>}makes a subformula that's in its entirety treated as an ordinary symbol. – egreg Oct 24 '18 at 20:00{<math>}? – Olivier Cailloux Oct 25 '18 at 09:23