Here is a proposal of 2 macros that draw the right angles.
They have 3 mandatory arguments: the point of intersection and the names of the two paths. The optional argument is used to transmit tikz options. I would have liked to group them into a single macro, but I didn't succeed.
They use the intersections and calc libraries of tikz.
% require \usetikzlibrary{intersections,calc}
\newcommand{\rightangleA}[4][]{
\begin{scope}
\path[name path=#2#3#4](#2) circle(6pt);
\path[name intersections={of=#2#3#4 and #3,name=i1}];
\path[name intersections={of=#2#3#4 and #4,name=i2}];
\draw[#1] (i1-1)to($(i1-1)+(i2-1)-(#2)$)to(i2-1)to(#2);
\end{scope}
}
\newcommand{\rightangleB}[4][]{
\begin{scope}
\path[name path=#2#3#4](#2) circle(6pt);
\path[name intersections={of=#2#3#4 and #3,name=i1}];
\path[name intersections={of=#2#3#4 and #4,name=i2}];
\draw[#1] (i1-2)to($(i1-2)+(i2-1)-(#2)$)to(i2-1)to(#2);
\end{scope}
}

\documentclass{article}
\usepackage[utf8]{inputenc}
\usepackage{tikz,pgfplots}
\usetikzlibrary{intersections,calc}
\pgfplotsset{compat=1.8}
\pgfplotsset{soldot/.style={color=black,only marks,mark=*}}
\pgfplotsset{holdot/.style={color=red,fill=white,very thick,only marks,mark=*}}
\newcommand{\rightangleA}[4][]{
\begin{scope}
\path[name path=#2#3#4](#2) circle(6pt);
\path[name intersections={of=#2#3#4 and #3,name=i1}];
\path[name intersections={of=#2#3#4 and #4,name=i2}];
\draw[#1] (i1-1)to($(i1-1)+(i2-1)-(#2)$)to(i2-1)to(#2);
\end{scope}
}
\newcommand{\rightangleB}[4][]{
\begin{scope}
\path[name path=#2#3#4](#2) circle(6pt);
\path[name intersections={of=#2#3#4 and #3,name=i1}];
\path[name intersections={of=#2#3#4 and #4,name=i2}];
\draw[#1] (i1-2)to($(i1-2)+(i2-1)-(#2)$)to(i2-1)to(#2);
\end{scope}
}
\begin{document}
\begin{center}
\begin{tikzpicture}
\begin{axis}[
legend pos=outer north east,
axis lines = center,
axis equal,
xticklabel style = {font=\tiny},
yticklabel style = {font=\tiny},
xlabel = $x$,
ylabel = $y$,
clip=false,
legend style={cells={align=left}},
legend cell align={left}
]
\addplot[thick,samples=80,name path=A] {-x/abs(x)^(2/3)}; % From https://tex.stackexchange.com/a/144463/152550
\addplot[thick,samples=80,name path=B] ({sqrt(16/3)*cos((x) r)}, {sqrt(16)*sin((x) r)});
\path[name intersections={of=A and B,by={c,d}}];% intersections of paths
\rightangleA{c}{A}{B}
\rightangleB[blue]{c}{A}{B}
\rightangleA[fill=red,thick]{d}{A}{B}
%\rightangleB{d}{A}{B}
\end{axis}
\end{tikzpicture}
\end{center}
\end{document}


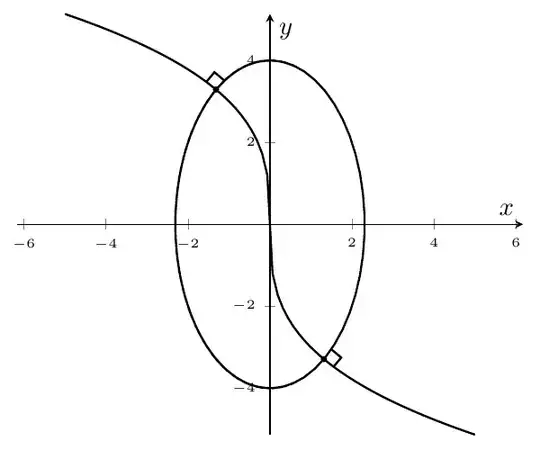



y^3 = x… – Ruixi Zhang Oct 27 '18 at 02:58y=-3*x/|x|^{2/3}, ory^3=x? – Oct 27 '18 at 03:18y-axis. Althought it should bey^3=x, as you said. – manooooh Oct 27 '18 at 04:11