How to draw a 3d horseshoe in TikZ

Question

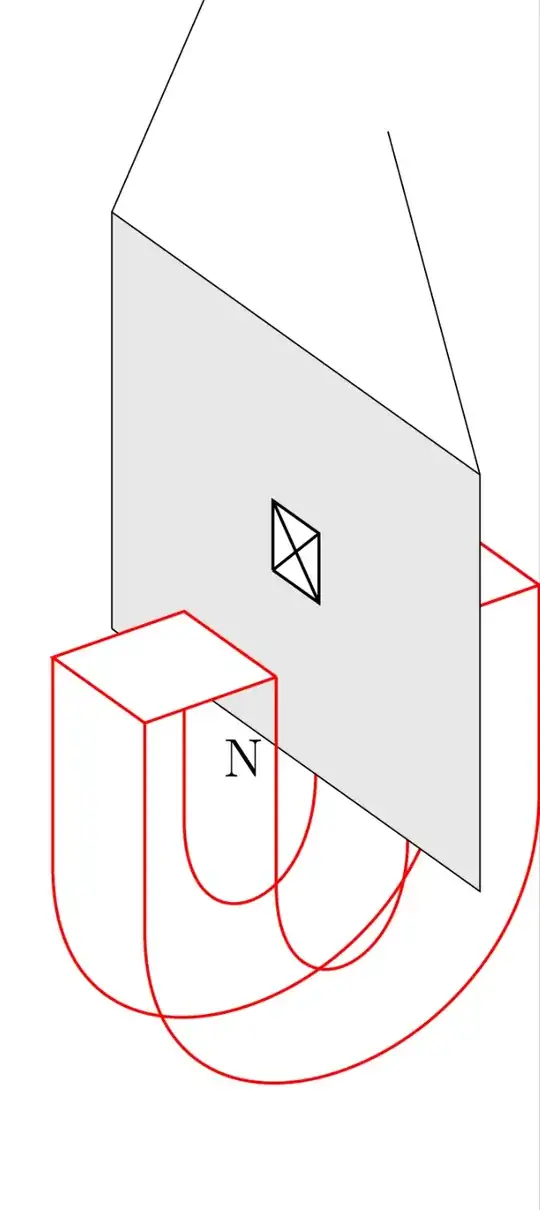
I am trying to draw an experimental setup involving a horseshoe magnet. I am having difficulty of hiding lines that should not appear, and I am unsure how to use shading to indicate the different surfaces. I would like the following TikZ picture to have the horseshoe (draw with thick and red options) to not be a net and be like a solid. Here is my code:

\documentclass{standalone}
\usepackage[svgnames]{xcolor}
\usepackage{tikz}
\usetikzlibrary{arrows.meta}
\usepackage{tikz-3dplot}

\begin{document}
\Large
\tdplotsetmaincoords{60}{55}
\begin{tikzpicture}[scale=15,tdplot_main_coords]
\tdplotsetrotatedcoords{0}{90}{90}
\begin{scope}[tdplot_rotated_coords]

\draw[thick,red] (-0.05,0.1,0.15) -- (-0.05,-0.05,0.15) .. controls +(0,-0.1,0) and +(0,-0.1,0) .. (0.05,-0.05,0.15) -- (0.05,0.1,0.15);

\draw[thick,red] (-0.15,0.1,0.15) -- (-0.15,-0.05,0.15) .. controls +(0,-0.2,0) and +(0,-0.2,0) .. (0.15,-0.05,0.15) -- (0.15,0.1,0.15);

\draw[thick,red] (-0.05,0.1,.25) -- (-0.05,-0.05,0.25) .. controls +(0,-0.1,0) and +(0,-0.1,0) .. (0.05,-0.05,0.25) -- (0.05,0.1,0.25) -- (0.15,0.1,0.25) -- (0.15,0.1,0.15);

\draw[thick,red] (-0.15,0.1,0.25) -- (-0.15,-0.05,0.25) .. controls +(0,-0.2,0) and +(0,-0.2,0) .. (0.15,-0.05,0.25) -- (0.15,0.1,0.25);

\draw[thick,red,fill=white] (0.05,0.1,0.25) -- (0.15,0.1,0.25) -- (0.15,0.1,0.15) -- (0.05,0.1,0.15) -- (0.05,0.1,0.25);

\draw[fill=black!10] (0,0,0) -- (0,0,.4) -- (0,.3,.4) -- (0,.3,0) -- (0,0,0);

\draw[thick,red] (-0.05,0.1,0.25) -- (-0.05,-0.05,0.25);

\draw[thick,red,fill=white] (-0.05,0.1,0.25) -- (-0.05,0.1,0.15) -- (-0.15,0.1,0.15) -- (-0.15,0.1,0.25) -- (-0.05,0.1,0.25);

\draw (0,.3,0) -- +(0,.2,.1);
\draw (0,.3,.4) -- +(0,.2,-0.1);
\node at (-0.075,.05,.25) {N};
\draw[thick,fill=white] (0,0.125,0.175) -- (0,0.175,0.175) -- (0,0.175,0.225) -- (0,0.125,0.225) -- (0,0.125,0.175);
\draw[thick] (0,0.125,0.175) -- (0,0.175,0.225);
\draw[thick] (0,0.175,0.175) -- (0,00.125,0.225);
\end{scope}
\end{tikzpicture}

\end{document}

Which produces

Also is it possible to make the curved inner and outer surfaces a particular shade of grey, and the other flat surfaces another shade of grey?

EDIT: Here is the final picture which would not have been possible without Marmot's answer (see below). It includes two more diagrams from the front and side. I think it is a good showcase of the abilities of TiKz-3d

\documentclass{standalone}
\usepackage[svgnames]{xcolor}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{3d}
% fix wrong implementation of xy canvas https://tex.stackexchange.com/a/48776/121799
\makeatletter
\tikzoption{canvas is xy plane at z}[]{%
  \def\tikz@plane@origin{\pgfpointxyz{0}{0}{#1}}%
  \def\tikz@plane@x{\pgfpointxyz{1}{0}{#1}}%
  \def\tikz@plane@y{\pgfpointxyz{0}{1}{#1}}%
  \tikz@canvas@is@plane
}
\tikzoption{canvas is yz plane at x}[]{%
  \def\tikz@plane@origin{\pgfpointxyz{#1}{0}{0}}%
  \def\tikz@plane@x{\pgfpointxyz{#1}{0}{0}}%
  \def\tikz@plane@y{\pgfpointxyz{#1}{1}{0}}%
  \tikz@canvas@is@plane}
\makeatother
\begin{document}
\tdplotsetmaincoords{60}{55}
\begin{tikzpicture}[scale=15]
\tdplotsetrotatedcoords{0}{90}{90}
\path[use as bounding box] (-0.1,-0.3) rectangle (0.6,0.4);
\begin{scope}[tdplot_rotated_coords]
% inner u  right half
\draw (0.05,0.1,0.15) -- (0.05,-0.05,0.15) --
plot[variable=\x,domain=360:180,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.15)
-- (-0.05,-0.05,0.15)  -- (-0.05,-0.05,0.25)  -- 
plot[variable=\x,domain=180:360,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.25)
-- (0.05,-0.05,0.25) -- (0.05,0.1,0.25) -- cycle;
\shade[top color=gray!20,bottom color=gray!80,middle color=gray!20] 
(0.05,0.1,0.15) -- (0.05,-0.05,0.15) --
plot[variable=\x,domain=360:180,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.15)
-- (-0.05,-0.05,0.15)  -- (-0.05,-0.05,0.25)  -- 
plot[variable=\x,domain=180:360,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.25)
-- (0.05,-0.05,0.25) -- (0.05,0.1,0.25) -- cycle;
% filled u in the front
\draw[fill=gray!30,canvas is xy plane at z=0.25]
(-0.15,0.1) -- (-0.15,-0.05) arc(180:360:0.15) -- (0.15,-0.05) -- (0.15,0.1) -- 
(0.05,0.1) -- (0.05,-0.05) arc(360:180:0.05) -- (-0.05,-0.05) -- (-0.05,0.1) -- cycle;
% top square on the right
\draw[fill=gray!10] (0.05,0.1,0.25) -- (0.15,0.1,0.25) -- (0.15,0.1,0.15) -- (0.05,0.1,0.15) -- (0.05,0.1,0.25);
% plane
\draw[fill=black!10] (0,0,0) -- (0,0,.4) -- (0,.3,.4) -- (0,.3,0) -- (0,0,0);
% left front triangle
\draw[fill=gray!30] (-0.15,0.1,0.25) -- (-0.05,0.1,0.25) -- (-0.05,-0.05,0.25);
% top square on the left
\draw[fill=gray!10] (-0.05,0.1,0.25) -- (-0.05,0.1,0.15) -- (-0.15,0.1,0.15) -- (-0.15,0.1,0.25) -- (-0.05,0.1,0.25);
% face on the left
\draw (-0.15,0.1,0.15) -- (-0.15,-0.05,0.15) --
plot[variable=\x,domain=180:225,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.15)
--
plot[variable=\x,domain=225:180,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.25)
--(-0.15,-0.05,0.25) -- (-0.15,0.1,0.25) -- cycle;
\shade[top color=gray!20,bottom color=gray!80,middle color=gray!20] 
(-0.15,0.1,0.15) -- (-0.15,-0.05,0.15) --
plot[variable=\x,domain=180:225,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.15)
--
plot[variable=\x,domain=225:180,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.25)
--(-0.15,-0.05,0.25) -- (-0.15,0.1,0.25) -- cycle;
% further elements 
\draw (0,.3,0) -- +(0,.2,.1);
\draw (0,.3,.4) -- +(0,.2,-0.1);
\node[canvas is xy plane at z=0.25,transform shape,scale=0.2] 
at (-0.1,0.05) {N};
\draw[thick,fill=white] (0,0.125,0.175) -- (0,0.175,0.175) -- (0,0.175,0.225) -- (0,0.125,0.225) -- (0,0.125,0.175);
\draw[thick] (0,0.125,0.175) -- (0,0.175,0.225);
\draw[thick] (0,0.175,0.175) -- (0,00.125,0.225);
\draw[thick,red,-latex] (0,0.125,0.175) -- +(-0.05,0,0) node[above] {$z$};
\draw[thick,blue,-latex] (0,0.125,0.175) -- +(0,.1,0) node[left] {$y$};
\draw[thick,-latex] (0,0.125,0.175) -- +(0,0,.1) node[below] {$x$};
\end{scope}

\tdplotsetmaincoords{90}{90}
\tdplotsetrotatedcoords{0}{90}{90}
\begin{scope}[xshift=0.4cm,yshift=0.2cm,tdplot_rotated_coords,scale=0.5]
\draw (0.05,0.1,0.15) -- (0.05,-0.05,0.15) --
plot[variable=\x,domain=360:180,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.15)
-- (-0.05,-0.05,0.15)  -- (-0.05,-0.05,0.25)  -- 
plot[variable=\x,domain=180:360,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.25)
-- (0.05,-0.05,0.25) -- (0.05,0.1,0.25) -- cycle;
\shade[top color=gray!20,bottom color=gray!80,middle color=gray!20] 
(0.05,0.1,0.15) -- (0.05,-0.05,0.15) --
plot[variable=\x,domain=360:180,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.15)
-- (-0.05,-0.05,0.15)  -- (-0.05,-0.05,0.25)  -- 
plot[variable=\x,domain=180:360,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.25)
-- (0.05,-0.05,0.25) -- (0.05,0.1,0.25) -- cycle;
% filled u in the front
\draw[fill=gray!30,canvas is xy plane at z=0.25]
(-0.15,0.1) -- (-0.15,-0.05) arc(180:360:0.15) -- (0.15,-0.05) -- (0.15,0.1) -- 
(0.05,0.1) -- (0.05,-0.05) arc(360:180:0.05) -- (-0.05,-0.05) -- (-0.05,0.1) -- cycle;
% top square on the right
\draw[fill=gray!10] (0.05,0.1,0.25) -- (0.15,0.1,0.25) -- (0.15,0.1,0.15) -- (0.05,0.1,0.15) -- (0.05,0.1,0.25);
% plane
\draw[fill=black!10] (0,0,0) -- (0,0,.4) -- (0,.3,.4) -- (0,.3,0) -- (0,0,0);
% left front triangle
\draw[fill=gray!30] (-0.15,0.1,0.25) -- (-0.05,0.1,0.25) -- (-0.05,-0.05,0.25);
% top square on the left
\draw[fill=gray!10] (-0.05,0.1,0.25) -- (-0.05,0.1,0.15) -- (-0.15,0.1,0.15) -- (-0.15,0.1,0.25) -- (-0.05,0.1,0.25);
% face on the left
\draw (-0.15,0.1,0.15) -- (-0.15,-0.05,0.15) --
plot[variable=\x,domain=180:225,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.15)
--
plot[variable=\x,domain=225:180,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.25)
--(-0.15,-0.05,0.25) -- (-0.15,0.1,0.25) -- cycle;
\shade[top color=gray!20,bottom color=gray!80,middle color=gray!20] 
(-0.15,0.1,0.15) -- (-0.15,-0.05,0.15) --
plot[variable=\x,domain=180:225,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.15)
--
plot[variable=\x,domain=225:180,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.25)
--(-0.15,-0.05,0.25) -- (-0.15,0.1,0.25) -- cycle;
% further elements 
\node[canvas is xy plane at z=0.25,transform shape,scale=0.2] 
at (-0.1,0.05) {N};
\draw[thick,red,-latex] (0,0.125,0.175) -- +(-0.1,0,0) node[above] {$z$};
\draw[thick,blue,-latex] (0,0.125,0.175) -- +(0,.1,0) node[left] {$y$};
\end{scope}

\tdplotsetmaincoords{90}{0}
\tdplotsetrotatedcoords{0}{90}{90}
\begin{scope}[xshift=0.3cm,yshift=-0.2cm,tdplot_rotated_coords,scale=0.5]
\draw (0.05,0.1,0.15) -- (0.05,-0.05,0.15) --
plot[variable=\x,domain=360:180,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.15)
-- (-0.05,-0.05,0.15)  -- (-0.05,-0.05,0.25)  -- 
plot[variable=\x,domain=180:360,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.25)
-- (0.05,-0.05,0.25) -- (0.05,0.1,0.25) -- cycle;
\shade[top color=gray!20,bottom color=gray!80,middle color=gray!20] 
(0.05,0.1,0.15) -- (0.05,-0.05,0.15) --
plot[variable=\x,domain=360:180,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.15)
-- (-0.05,-0.05,0.15)  -- (-0.05,-0.05,0.25)  -- 
plot[variable=\x,domain=180:360,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.25)
-- (0.05,-0.05,0.25) -- (0.05,0.1,0.25) -- cycle;
% filled u in the front
\fill[gray!30,canvas is xy plane at z=0.25]
(-0.15,0.1) -- (-0.15,-0.05) arc(180:360:0.15) -- (0.15,-0.05) -- (0.15,0.1) -- 
(0.05,0.1) -- (0.05,-0.05) arc(360:180:0.05) -- (-0.05,-0.05) -- (-0.05,0.1) -- cycle;
% top square on the right
\draw[fill=gray!10] (0.05,0.1,0.25) -- (0.15,0.1,0.25) -- (0.15,0.1,0.15) -- (0.05,0.1,0.15) -- (0.05,0.1,0.25);
% plane
\draw[fill=black!10] (0,0,0) -- (0,0,.4) -- (0,.3,.4) -- (0,.3,0) -- (0,0,0);
% left front triangle
\draw[fill=gray!30] (-0.15,0.1,0.25) -- (-0.05,0.1,0.25) -- (-0.05,-0.05,0.25);
% top square on the left
\draw[fill=gray!10] (-0.05,0.1,0.25) -- (-0.05,0.1,0.15) -- (-0.15,0.1,0.15) -- (-0.15,0.1,0.25) -- (-0.05,0.1,0.25);
% face on the left
\draw (-0.15,0.1,0.15) -- (-0.15,-0.05,0.15) --
plot[variable=\x,domain=180:225,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.15)
--
plot[variable=\x,domain=225:180,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.25)
--(-0.15,-0.05,0.25) -- (-0.15,0.1,0.25) -- cycle;
\shade[top color=gray!20,bottom color=gray!80,middle color=gray!20] 
(-0.15,0.1,0.15) -- (-0.15,-0.05,0.15) --
plot[variable=\x,domain=180:225,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.15)
--
plot[variable=\x,domain=225:180,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.25)
--(-0.15,-0.05,0.25) -- (-0.15,0.1,0.25) -- cycle;
% further elements 
\draw[thick,fill=white] (0,0.125,0.175) -- (0,0.175,0.175) -- (0,0.175,0.225) -- (0,0.125,0.225) -- (0,0.125,0.175);
\draw[thick] (0,0.125,0.175) -- (0,0.175,0.225);
\draw[thick] (0,0.175,0.175) -- (0,00.125,0.225);
\draw[thick,blue,-latex] (0,0.125,0.175) -- +(0,.1,0) node[left] {$y$};
\draw[thick,-latex] (0,0.125,0.175) -- +(0,0,.1) node[below] {$x$};
\node[anchor=center,scale=1.5] at (-0.25,0.05,0.2) {N};
\end{scope}
\end{tikzpicture}
\end{document}

Note that the labelled axis are not in the correct order, the x and z axis have been swapped because that is how I referenced them in my formulae for my report.

Answer 1

Does that come close to what you had in mind?

\documentclass[border=3.14mm]{standalone}
\usepackage[svgnames]{xcolor}
\usepackage{tikz}
\usepackage{tikz-3dplot}

\begin{document}
\tdplotsetmaincoords{60}{55}
\begin{tikzpicture}[scale=15,tdplot_main_coords]
\tdplotsetrotatedcoords{0}{90}{90}
\begin{scope}[tdplot_rotated_coords]
% filled u in the back
\draw[thick,red,fill=gray!30] (-0.15,0.1,0.15) -- (-0.15,-0.05,0.15) .. controls +(0,-0.2,0)
and +(0,-0.2,0) .. (0.15,-0.05,0.15) -- (0.15,0.1,0.15) -- 
(0.05,0.1,0.15) -- (0.05,-0.05,0.15) .. controls +(0,-0.1,0) and +(0,-0.1,0) .. 
(-0.05,-0.05,0.15) -- (-0.05,0.1,0.15) -- cycle;
% inner u  right half
\draw[thick,red,top color=gray!20,bottom color=gray!80,middle color=gray!20] (0.05,0.1,0.15) -- (0.05,-0.05,0.15) .. controls +(0,-0.1,0)
and +(0,-0.1,0) .. (-0.05,-0.05,0.15) -- (-0.05,-0.05,0.25)
.. controls +(0,-0.2,0) and +(0,-0.2,0) .. (0.05,-0.05,0.25)
-- (0.05,0.1,0.25) -- cycle;
% filled u in the front
\draw[thick,red,fill=gray!30] (-0.15,0.1,0.25) -- (-0.15,-0.05,0.25) .. controls +(0,-0.2,0)
and +(0,-0.2,0) .. (0.15,-0.05,0.25) -- (0.15,0.1,0.25) -- 
(0.05,0.1,0.25) -- (0.05,-0.05,0.25) .. controls +(0,-0.1,0) and +(0,-0.1,0) .. 
(-0.05,-0.05,0.25) -- (-0.05,0.1,0.25) -- cycle;
% top square on the right
\draw[thick,red,fill=gray!10] (0.05,0.1,0.25) -- (0.15,0.1,0.25) -- (0.15,0.1,0.15) -- (0.05,0.1,0.15) -- (0.05,0.1,0.25);
% plane
\draw[fill=black!10] (0,0,0) -- (0,0,.4) -- (0,.3,.4) -- (0,.3,0) -- (0,0,0);
% left front triangle
\draw[thick,red,fill=gray!30] (-0.15,0.1,0.25) -- (-0.05,0.1,0.25) -- (-0.05,-0.05,0.25);
% top square on the left
\draw[thick,red,fill=gray!10] (-0.05,0.1,0.25) -- (-0.05,0.1,0.15) -- (-0.15,0.1,0.15) -- (-0.15,0.1,0.25) -- (-0.05,0.1,0.25);
% face on the left
\draw[thick,red,top color=gray!20,bottom color=gray!80,middle color=gray!20] 
(-0.15,0.1,0.15) -- (-0.15,-0.05,0.15)
to[out=-90,in=150] (-0.1,-0.165,0.15)-- (-0.1,-0.165,0.25) 
to[out=150,in=-90] (-0.15,-0.05,0.25) -- (-0.15,0.1,0.25) -- cycle;
% further elements 
\draw (0,.3,0) -- +(0,.2,.1);
\draw (0,.3,.4) -- +(0,.2,-0.1);
\node[font=\Large] at (-0.075,.05,.25) {N};
\draw[thick,fill=white] (0,0.125,0.175) -- (0,0.175,0.175) -- (0,0.175,0.225) -- (0,0.125,0.225) -- (0,0.125,0.175);
\draw[thick] (0,0.125,0.175) -- (0,0.175,0.225);
\draw[thick] (0,0.175,0.175) -- (0,00.125,0.225);
\end{scope}
\end{tikzpicture}
\end{document}

Remarks:

• I guess the U-shapes could be slightly improved by either drawing arcs with the tikz-3dplot methods (which work fine, however, I find the syntax not optimal but this is just my taste) or the 3d library by switching to appropriate planes and drawing half-circle arcs.
• It generally helps in cases in which the graph is slightly more complex to add comments in the TeX file that indicate which line draws what. This will prevent poor marmots from drawing single stretches in blue and thus inferring what they do. ;-)

In what follows, I present a slightly different approach in which among other things the 3d library is employed. The main purpose of this is to produce an animation that shows step by step how the graphics is produced, and where I cheat. (EDIT: Kicked out the unnecessary U in the back, big thanks to Henri Menke!)

\documentclass{beamer}
\beamertemplatenavigationsymbolsempty
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{3d}
% fix wrong implementation of xy canvas https://tex.stackexchange.com/a/48776/121799
\makeatletter
\tikzoption{canvas is xy plane at z}[]{%
  \def\tikz@plane@origin{\pgfpointxyz{0}{0}{#1}}%
  \def\tikz@plane@x{\pgfpointxyz{1}{0}{#1}}%
  \def\tikz@plane@y{\pgfpointxyz{0}{1}{#1}}%
  \tikz@canvas@is@plane
}
\makeatother
\begin{document}
\begin{frame}[t]
\frametitle{\only<1>{Draw U in the back}%
\only<2>{Draw inner face}%
\only<3>{Draw U in the front}%
\only<4>{Draw top square on the right}%
\only<5>{Draw plane}%
\only<6>{Restore U in the front by filling an appropriate triangle}%
\only<7>{Draw top square on the left}%
\only<8>{Shade face on the left}%
\only<9>{Add the remaining elements}%
}
\tdplotsetmaincoords{60}{55}
\begin{tikzpicture}[scale=10]
\tdplotsetrotatedcoords{0}{90}{90}
\path[use as bounding box] (-0.1,-0.3) rectangle (0.3,0.45);
\begin{scope}[tdplot_rotated_coords]
% filled u in the back
\fill[gray!30,canvas is xy plane at z=0.15]
(-0.15,0.1) -- (-0.15,-0.05) arc(180:360:0.15) -- (0.15,-0.05) -- (0.15,0.1) -- 
(0.05,0.1) -- (0.05,-0.05) arc(360:180:0.05) -- (-0.05,-0.05) -- (-0.05,0.1) -- cycle;
\pause
% inner u  right half
\shade[top color=gray!20,bottom color=gray!80,middle color=gray!20] 
(0.05,0.1,0.15) -- (0.05,-0.05,0.15) --
plot[variable=\x,domain=360:180,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.15)
-- (-0.05,-0.05,0.15)  -- (-0.05,-0.05,0.25)  -- 
plot[variable=\x,domain=180:360,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.25)
-- (0.05,-0.05,0.25) -- (0.05,0.1,0.25) -- cycle;
\pause
% filled u in the front
\fill[gray!30,canvas is xy plane at z=0.25]
(-0.15,0.1) -- (-0.15,-0.05) arc(180:360:0.15) -- (0.15,-0.05) -- (0.15,0.1) -- 
(0.05,0.1) -- (0.05,-0.05) arc(360:180:0.05) -- (-0.05,-0.05) -- (-0.05,0.1) -- cycle;
\pause
% top square on the right
\fill[gray!10] (0.05,0.1,0.25) -- (0.15,0.1,0.25) -- (0.15,0.1,0.15) -- (0.05,0.1,0.15) -- (0.05,0.1,0.25);
\pause
% plane
\draw[fill=black!10] (0,0,0) -- (0,0,.4) -- (0,.3,.4) -- (0,.3,0) -- (0,0,0);
\pause
% left front triangle
\fill[gray!30] (-0.15,0.1,0.25) -- (-0.05,0.1,0.25) -- (-0.05,-0.05,0.25);
\pause
% top square on the left
\fill[gray!10] (-0.05,0.1,0.25) -- (-0.05,0.1,0.15) -- (-0.15,0.1,0.15) -- (-0.15,0.1,0.25) -- (-0.05,0.1,0.25);
\pause
% face on the left
\shade[top color=gray!20,bottom color=gray!80,middle color=gray!20] 
(-0.15,0.1,0.15) -- (-0.15,-0.05,0.15) --
plot[variable=\x,domain=180:225,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.15)
--
plot[variable=\x,domain=225:180,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.25)
--(-0.15,-0.05,0.25) -- (-0.15,0.1,0.25) -- cycle;
\pause
% further elements 
\draw (0,.3,0) -- +(0,.2,.1);
\draw (0,.3,.4) -- +(0,.2,-0.1);
\node[canvas is xy plane at z=0.25,transform shape,scale=0.2] 
at (-0.1,0.05) {N};
\draw[thick,fill=white] (0,0.125,0.175) -- (0,0.175,0.175) -- (0,0.175,0.225) -- (0,0.125,0.225) -- (0,0.125,0.175);
\draw[thick] (0,0.125,0.175) -- (0,0.175,0.225);
\draw[thick] (0,0.175,0.175) -- (0,00.125,0.225);
\end{scope}
\end{tikzpicture}
\end{frame}
\end{document}

And if you remove the beamer commands from this, you'll get

\documentclass{standalone}
\usepackage[svgnames]{xcolor}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{3d}
% fix wrong implementation of xy canvas https://tex.stackexchange.com/a/48776/121799
\makeatletter
\tikzoption{canvas is xy plane at z}[]{%
  \def\tikz@plane@origin{\pgfpointxyz{0}{0}{#1}}%
  \def\tikz@plane@x{\pgfpointxyz{1}{0}{#1}}%
  \def\tikz@plane@y{\pgfpointxyz{0}{1}{#1}}%
  \tikz@canvas@is@plane
}
\makeatother
\begin{document}
\tdplotsetmaincoords{60}{55}
\begin{tikzpicture}[scale=15]
\tdplotsetrotatedcoords{0}{90}{90}
\path[use as bounding box] (-0.1,-0.3) rectangle (0.3,0.45);
\begin{scope}[tdplot_rotated_coords]
% inner u  right half
\shade[top color=gray!20,bottom color=gray!80,middle color=gray!20] 
(0.05,0.1,0.15) -- (0.05,-0.05,0.15) --
plot[variable=\x,domain=360:180,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.15)
-- (-0.05,-0.05,0.15)  -- (-0.05,-0.05,0.25)  -- 
plot[variable=\x,domain=180:360,smooth] ({0.05*cos(\x)},{-0.05+0.05*sin(\x)},0.25)
-- (0.05,-0.05,0.25) -- (0.05,0.1,0.25) -- cycle;
% filled u in the front
\fill[gray!30,canvas is xy plane at z=0.25]
(-0.15,0.1) -- (-0.15,-0.05) arc(180:360:0.15) -- (0.15,-0.05) -- (0.15,0.1) -- 
(0.05,0.1) -- (0.05,-0.05) arc(360:180:0.05) -- (-0.05,-0.05) -- (-0.05,0.1) -- cycle;
% top square on the right
\fill[gray!10] (0.05,0.1,0.25) -- (0.15,0.1,0.25) -- (0.15,0.1,0.15) -- (0.05,0.1,0.15) -- (0.05,0.1,0.25);
% plane
\draw[fill=black!10] (0,0,0) -- (0,0,.4) -- (0,.3,.4) -- (0,.3,0) -- (0,0,0);
% left front triangle
\fill[gray!30] (-0.15,0.1,0.25) -- (-0.05,0.1,0.25) -- (-0.05,-0.05,0.25);
% top square on the left
\fill[gray!10] (-0.05,0.1,0.25) -- (-0.05,0.1,0.15) -- (-0.15,0.1,0.15) -- (-0.15,0.1,0.25) -- (-0.05,0.1,0.25);
% face on the left
\shade[top color=gray!20,bottom color=gray!80,middle color=gray!20] 
(-0.15,0.1,0.15) -- (-0.15,-0.05,0.15) --
plot[variable=\x,domain=180:225,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.15)
--
plot[variable=\x,domain=225:180,smooth] ({0.15*cos(\x)},{-0.05+0.15*sin(\x)},0.25)
--(-0.15,-0.05,0.25) -- (-0.15,0.1,0.25) -- cycle;
% further elements 
\draw (0,.3,0) -- +(0,.2,.1);
\draw (0,.3,.4) -- +(0,.2,-0.1);
\node[canvas is xy plane at z=0.25,transform shape,scale=0.2] 
at (-0.1,0.05) {N};
\draw[thick,fill=white] (0,0.125,0.175) -- (0,0.175,0.175) -- (0,0.175,0.225) -- (0,0.125,0.225) -- (0,0.125,0.175);
\draw[thick] (0,0.125,0.175) -- (0,0.175,0.225);
\draw[thick] (0,0.175,0.175) -- (0,00.125,0.225);
\end{scope}
\end{tikzpicture}
\end{document}