Tikz and Secant Line diagram

Question

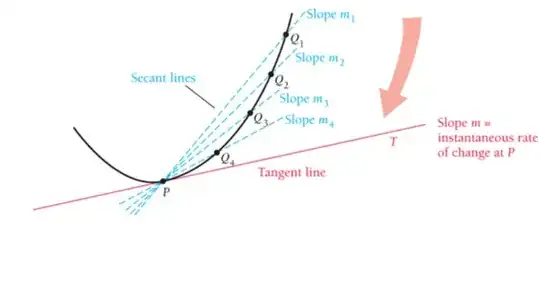
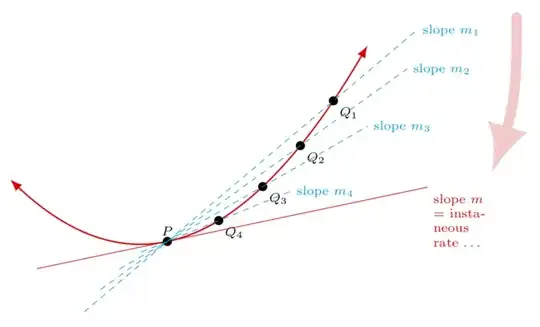
Hi I am looking for feedback to improve an existing program PLUS advice for a desired diagram in the same direction.

Here is my minimal example:

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{decorations.pathreplacing}

\begin{document}
\begin{center}
\begin{tikzpicture}[scale=1.75,cap=round]
\tikzset{axes/.style={}}
%\draw[style=help lines,step=1cm, dotted] (-5.25,-5.25) grid (5.25,5.25);
% The graphic
\begin{scope}[style=axes]
\draw[->] (-.5,0) -- (4.5,0) node[below] {$x$};
\draw[->] (0,-.5)-- (0,3) node[left] {$y$};
\foreach \x/\xtext in {1.5/x_{1}, 3/x_{2}}
 \draw[xshift=\x cm] (0pt,2pt) -- (0pt,-2pt) 
node[below,fill=white,font=\normalsize]
  {$\xtext$};    
\foreach \y/\ytext in {1/y_{1}=f(x_{1}), 2.125/y_{1}=f(x_{2})}
  \draw[yshift=\y cm] (2pt,0pt) -- (-2pt,0pt) 
  node[left,fill=white,font=\normalsize]
  {$\ytext$};
  %%%
 \draw[domain=.5:3.25,smooth,variable=\x,red,<->,thick] plot ({\x},{.5*(\x-1.5)*(\x-1.5)+1});
  %%%
\filldraw[black] (1.5,1) circle (1pt) node[above] {\scriptsize $P$};
\filldraw[black] (3,2.125) circle (1pt) node[left] {\scriptsize $Q$};
\draw[thick,blue!50,shorten >=-.5cm,shorten <=-.5cm] (1.5,1)--(3,2.125) 
node[midway,left] {\scriptsize Secant Line};
 %%%
 \draw[blue!50,thick,dashed] (1.5,1)--(3,1)--(3,2.125);
 \draw[blue!50] (3,1.1)--(2.9,1.1)--(2.9,1);
 \draw[decoration={brace,mirror,raise=5pt},decorate,blue!50]
    (1.5,-.250) -- node[below=6pt] {$x_{2}-x_{1}$} (3,-.250);
 \draw[decoration={brace,mirror, raise=5pt},decorate,blue!50]
    (3,1) -- node[right=6pt] {$f(x_{2})-f(x_{1})$} (3,2.215);
 %%%
\filldraw[black] (1.5,1) circle (1pt) node[above] {\scriptsize $P$};
\filldraw[black] (3,2.125) circle (1pt) node[left] {\scriptsize $Q$};
\end{scope}
\end{tikzpicture}
\end{center}
\end{document}

This will Output

I am trying to go here with the picture:

This is a bit beyond my programming skills I think ? PLease all suggestions welcome

Answer 1

I refactored the yesterday answer and added some new features.

\documentclass[pstricks,border=12pt,12pt]{standalone}
\usepackage{pstricks-add,pst-eucl}


\def\f(#1){((#1+3)/3+sin(#1+3))}
\def\fp(#1){Derive(1,\f(#1))}
\psset{unit=2}

\begin{document}
\multido{\r=2.0+-.1}{19}{%
\begin{pspicture}[algebraic](-1.6,-.6)(4.4,3.4)
    \psaxes[ticks=none,labels=none]{->}(0,0)(-1.6,-.6)(4.1,3.1)[$x$,0][$y$,90]
    \psplot[linecolor=red,linewidth=2pt]{-1}{3.9}{\f(x)}
    %
    \psplotTangent[linecolor=blue]{1.6}{1}{\f(x)}
    \psplotTangent[linecolor=cyan,Derive={-1/\fp(x)}]{1.6}{.5}{\f(x)}
    %
    \pstGeonode[PosAngle={135,90}]
        (*1.6 {\f(x)}){A}
        (*{1.6 \r\space add} {\f(x)}){B}
    \pstGeonode[PosAngle={-120,-60},PointName={x_1,x_2},PointNameSep=8pt]
        (A|0,0){x1}
        (B|0,0){x2}
    \pstGeonode[PosAngle={210,150},PointName={f(x_1),f(x_2)},PointNameSep=20pt]
        (0,0|A){fx1}
        (0,0|B){fx2}
    \pcline[nodesep=-.5,linecolor=green](A)(B)
    %
    \psset{linestyle=dashed}
    \psCoordinates(A)
    \psCoordinates(B)
    %
    \psset{linecolor=gray,linestyle=dashed,labelsep=4pt,arrows=|*-|*,offset=-16pt}
    \pcline(x1)(x2)
    \nbput{$x_2-x_1$}
    \pcline(fx2)(fx1)
    \nbput{$f(x_2)-f(x_1)$}
\end{pspicture}}
\end{document}

Secant, tangent, and normal lines are given free of charge!

Answer 2

With decorations.markings you can mark coordinates along the path, which then allow you to draw tangents. Note that drawing tangents has already been discussed at length in this nice answer, and I am implicitly using the same approach. However, my code is an attempt to have a unified treatment of both of your requests, i.e. tangent and secants, so at first sight it looks quite different.

\documentclass[tikz,border=3.14mm]{standalone}
\usetikzlibrary{decorations.pathreplacing,decorations.markings,calc,arrows.meta,bending}

\begin{document}
\begin{tikzpicture}[scale=2.5,cap=round,mark pos/.style args={#1/#2}{%
postaction={decorate,decoration={markings,%
mark=at position #1 with {
\coordinate (#2);}}}}]
\tikzset{axes/.style={}}
%\draw[style=help lines,step=1cm, dotted] (-5.25,-5.25) grid (5.25,5.25);
% The graphic
\begin{scope}[style=axes]
  %%%
  \pgfmathsetmacro{\posP}{0.38}
 \draw[red,{Latex[bend]}-{Latex[bend]},thick,mark
 pos/.list={\posP-0.005/p-0,\posP/P,\posP+0.005/p-2,0.5/q-4,0.62/q-3,0.74/q-2,0.86/q-1}] plot[domain=.5:3.25,samples=101,variable=\x] ({\x},{.5*(\x-1.5)*(\x-1.5)+1});
 \draw[red] let \p1=($(p-2)-(p-0)$),\n1={(\y1/\x1)*(1cm/1pt)}
 in ($(P)-1*(1,\n1)$) -- ($(P)+2*(1,\n1)$) node[right,anchor=north
 west,font=\scriptsize,text width=1cm]{slope $m$ $=$ instaneous rate \dots};
 \fill (P) circle (1pt) node[above,font=\scriptsize] {$P$};
 \foreach \X in {1,...,4}
 {\fill (q-\X) circle (1pt) node[below right,font=\scriptsize] {$Q_\X$};
 \path (P) -- (q-\X) coordinate[pos=-0.5] (L-\X) coordinate[pos={1.2+\X*0.3}] (R-\X);
 \draw[cyan,dashed] (L-\X) -- (R-\X) node[right,font=\scriptsize] (m\X) {slope $m_\X$}; }
 \draw[line width=2mm,-{Latex[bend]},red!20] ($(m1)+(0.5,0.1)$)
 to[out=-90,in=65] ++ (-0.2,-1.2);
  %%%
 %%%
\end{scope}
\end{tikzpicture}
\end{document}

Answer 3

I see that @marmot has already given you the solution. This is just another way of doing it. Just an attempt to do it without using any extra libraries.

\documentclass[border=1cm]{standalone}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}[declare function={func(\y) = 0.1*(\y-5)*(\y-5)+1;}]
\draw[domain=2:15,smooth,variable=\x,thick] plot ({\x},{func(\x)});
\draw[fill] (6.4,{func(6.4)})node[below]{p}circle (2pt)coordinate(p);
\foreach[count=\i] \x in {8.0,9.6,...,14.4}{
    \draw[fill] (\x,{0.1*(\x-5)*(\x-5)+1})node[below]{Q$_\i$} circle (2pt)coordinate(Q\i);
    \draw[thick,blue!80,dashed,shorten >=-2cm,shorten <=-2cm] (p) -- (Q\i)node[right=0.7cm](m\i){slope m$_\i$};
    }
\draw[thick,red!70,shorten >=-9cm,shorten <=-4cm] (p) -- (6.401,{func(6.401)});
\draw[-latex,line width=4mm,red!20] (m4.south east) to[out=-100, in=25] (m2.south east)node[below,anchor=north west,red]{slope $m=\ldots$};
\end{tikzpicture}
\end{document}