The picture shows a normal linear regression.
Although it is easy to compute on paper, I have no idea how to code a linear regression in order to get an output shown as in the picture.
I would be very pleased if anyone could help me.
I have already tried {tikzpicture} etc. but it does not work out that good as pleased.
Motivated by AndréC's comments... ;-)
\documentclass{article}
\usepackage{tikzlings}
\usepackage{pgfplots, pgfplotstable}
\pgfplotsset{compat=1.16}
\pgfplotstableread{
X Y
1 2
2 2.5
3 6
3 6.5
4 10
5 8
}\datatable
\begin{document}
\pgfplotsset{every axis legend/.append style={
cells={anchor=west}}}
\begin{tikzpicture}
\begin{axis}[legend pos=north west,xmin=0,xmax=7,
ymin=0,ymax=15,enlargelimits=0.1]
\addplot[only marks, mark=*] table[x=X,y=Y] {\datatable};
\addlegendentry{$y_i$}
\addplot[draw=none,color=red] table [
x=X,
y={create col/linear regression={y=Y}},
] {\datatable};
\xdef\slope{\pgfplotstableregressiona}
\xdef\offset{\pgfplotstableregressionb}
\addplot[no marks,color=red,domain=-2:9] {\slope*x+\offset};
\addlegendentry{$f(x_i)=\beta_0+\beta_1x_i$}
\coordinate (aux1) at (2,{\slope*2+\offset});
\coordinate (aux2) at (2,2.5);
\end{axis}
\draw[latex-latex,red] (aux1) -- (aux2)
node[midway,right,text=black,font=\sffamily]{St\"orterm:
$\varepsilon_i=y_i-f(x_i)$};
\marmot[xshift=8cm,whiskers,teeth,crystal ball]
\end{tikzpicture}
\end{document}
And this is motivated by Sebastiano's comment.
\documentclass{article}
\usepackage{tikzlings}
\usepackage{pgfplots, pgfplotstable}
\pgfplotsset{compat=1.16}
\pgfplotstableread{
X Y
1 2
2 2.5
3 6
3 6.5
4 10
5 8
}\datatable
% pgfmanual p. 1087
\pgfdeclareradialshading{ballshading}{\pgfpoint{-10bp}{10bp}}
{color(0bp)=(cyan!15!white); color(9bp)=(cyan!75!white);
color(18bp)=(cyan!70!black); color(25bp)=(cyan!50!black); color(50bp)=(black)}
\pgfdeclareplotmark{crystal ball}{\pgfpathcircle{\pgfpoint{0ex}{0ex}}{1ex}
\pgfshadepath{ballshading}{0}
\pgfusepath{}}
\begin{document}
\pgfplotsset{every axis legend/.append style={
cells={anchor=west}}}
\begin{tikzpicture}
\begin{axis}[legend pos=north west,xmin=0,xmax=7,
ymin=0,ymax=15,enlargelimits=0.1]
\addplot[only marks, mark=crystal ball,opacity=0.7] table[x=X,y=Y] {\datatable};
\addlegendentry{$y_i$}
\addplot[draw=none,color=red] table [
x=X,
y={create col/linear regression={y=Y}},
] {\datatable};
\xdef\slope{\pgfplotstableregressiona}
\xdef\offset{\pgfplotstableregressionb}
\addplot[no marks,color=red,domain=-2:9] {\slope*x+\offset};
\addlegendentry{$f(x_i)=\beta_0+\beta_1x_i$}
\coordinate (aux1) at (2,{\slope*2+\offset});
\coordinate (aux2) at (2,2.5);
\end{axis}
\draw[latex-latex,red] (aux1) -- (aux2)
node[midway,right,text=black,font=\sffamily]{St\"orterm:
$\varepsilon_i=y_i-f(x_i)$};
\marmot[xshift=8cm,whiskers,teeth,crystal ball]
\end{tikzpicture}
\end{document}
tikzpicture? In particular, how did roughly you make that ball with varying translucency?
– Code Doggo
Dec 01 '18 at 18:31
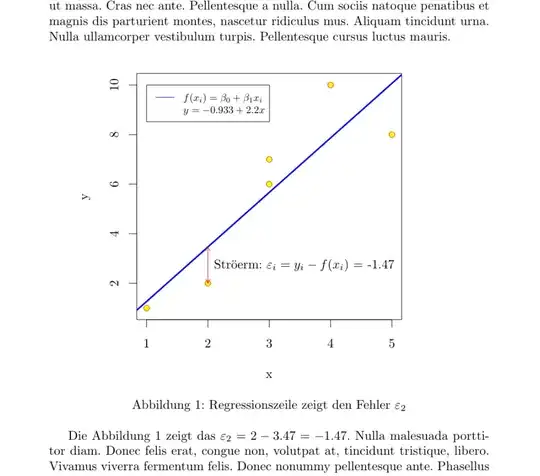
With R and knitr this plot is relatively simple. However, the MWE is a bit complex to show automatically the actual coefficients (intercept, slope and error) as well as to place legend, arrow and label automatically, so one can change the values at some range (for instance, the second y from 2 to -3) and still have a correct output in all aspects, even in the text out of the figure.
\documentclass{article}
\usepackage{lipsum}
\usepackage[german]{babel}
\usepackage[utf8]{inputenc}
<<Daten,echo=F>>=
df <- data.frame(x=c(1,2,3,3,4,5),y=c(1,2,6,7,10,8))
@
\begin{document}
\lipsum[2]
<<Streudiagramm,echo=F,dev="tikz", fig.cap="Regressionszeile zeigt den Fehler $\\varepsilon_2$", fig.width=4.2, fig.height=3.5,fig.align='center',fig.pos="h">>=
par(mar=c(4,4,1,4)) # optional, just to crop
mod <- lm(df$y~df$x)
with(df,plot(x,y, pch=21, col="red",bg="yellow",ylim=c(min(df$y-.1),max(df$y+.1))))
abline(mod,col="blue",lwd=3)
legend(1, max(df$y), legend=c("$f(x_i)=\\beta_0+\\beta_1x_i$",
paste("$y=",
signif(mod$coefficients[1],3),"+",
signif(mod$coefficients[2],3),"x$")),
col=c("blue","white"), lty=1:2, cex=0.8)
arrows(df$x[2],df$y[2],df$x[2],predict(mod)[2], length=0.05, col =2, code=3)
text(df$x[2]+.1,mean(c(df$y[2],predict(mod)[2])),paste('Str\\"{o}erm: $\\varepsilon_i=y_i-f(x_i)$ =',signif(df$y[2]-predict(mod)[2],3)),adj=0)
@
Die Abbildung \ref{fig:Streudiagramm} zeigt das $\varepsilon_2 =
\Sexpr{signif(df$y[2],3)} -
\Sexpr{signif(predict(mod)[2],3)} =
\Sexpr{signif(df$y[2]-(mod$coefficients[1]+(mod$coefficients[2]*df$x[2])),3)} $.
\lipsum[3]
\end{document}
pgfplotsallows you to do this, see p 396Fitting Lines - Regression: https://ctan.org/pkg/pgfplots – AndréC Dec 01 '18 at 13:15pstricks(more preciselypst-plot) defines aplotstyle=LSMfor data files. – Bernard Dec 01 '18 at 13:34how she can create this graph. If she knew, she wouldn't have asked that question. – AndréC Dec 01 '18 at 13:39TikZor one of its descendants. She wants to know which packages allow her to do what she wants because she taggedgraphics(and notTikZ). I told herpgfplots, Bernard told herpstrics. – AndréC Dec 01 '18 at 15:15building a normal linear regression. Please modify this title to make the question easier to search with a search engine by clicking on theeditbutton. – AndréC Dec 02 '18 at 05:44