Solvent-accessible and -excluded surface

Question

I would like to reproduce this graph in TikZ:

I'm not new to TikZ and I can imagine how to draw the lines in green and black, but I cannot imagine how to draw the line in red (which is draw by th borders of the probe sphere rolling on the green atoms).

Perhaps you could then add a sample of the black and green lines, then people will have time to focus on getting you the red lines. — Phelype Oleinik, Dec 04 '18 at 21:21
@PhelypeOleinik: I wanted to get the whole concept before starting to draw (and start over). I would draw the green and black line with superpostion of filled circles of different radii. — Kyle_the_hacker, Dec 04 '18 at 21:35
I guess that the red line requires sort of a "theory" that determines the point at which the red line departs from the circle. It might be related to the position where certain tangents hit the circle. Do you have such a "theory" or prescription? Looking at the pic again, what determines the radius of the probe sphere? — , Dec 04 '18 at 21:39
@marmot: the radius of the probe sphere is fixed, the sphere rolls on the green atoms; the sphere moves in such a way that its center stays on the black line. — Kyle_the_hacker, Dec 04 '18 at 21:49

score 7 · Accepted Answer · 2018-12-08T07:29:34.043

Here is a proposal (essentially repeating the tricks from here). Each of the arcs is computed from the probe sphere touching two neighboring atoms. The corresponding path is computed with merge circles. The paths along the boundaries of the atoms are done with path along circle. And this answer comes also with the styles get circle intersections and midcircle that allows one to conveniently wipe out the overlaps.

\documentclass[tikz,border=3.14mm]{standalone}
\usetikzlibrary{calc}
\tikzset{merge circles/.style n args={4}{insert path={
let \p1=(#1),\p2=(#2),\n1={veclen(\x1-\x2,\y1-\y2)*1pt/1cm},
\n2={atan2(\y2-\y1,\x2-\x1)},
\n3={mangle((#4+\ProbeSphereRadius),\n1,(#3+\ProbeSphereRadius))},
\n4={mangle(\n1,(#4+\ProbeSphereRadius),(#3+\ProbeSphereRadius))}
in %\pgfextra{\typeout{\n1,\n2,\n3,\n4}}
($(#1)+(+\n2+\n3:#3)$) arc(180+\n2+\n3:180+\n2+\n3+\n4:\ProbeSphereRadius)
}},
path along circle/.style args={with center #1 from #2 to #3}{insert path={
let \p1=($(#2)-(#1)$), \p2=($(#3)-(#1)$),
\n1={atan2(\y1,\x1)}, \n2={atan2(\y2,\x2)}, \n3={veclen(\x1,\y1)},
\n5={ifthenelse(\n2<\n1,\n2,\n2-360)}
in %\pgfextra{\typeout{\n1,\n2,\n5}}
 (#2) arc(\n1:\n5:\n3)}},
get circle intersections/.style n args={6}{insert path={
let \p1=(#1),\p2=(#2),\n1={veclen(\x1-\x2,\y1-\y2)*1pt/1cm},
\n2={atan2(\y2-\y1,\x2-\x1)},
\n3={mangle(#4,\n1,#3)},
\n4={mangle(\n1,#4,#3)}
in ($(#1)+(+\n2+\n3:#3)$) coordinate (#5) 
($(#1)+(+\n2-\n3:#3)$) coordinate (#6)}},
midcircle/.style args={of #1 and #2}{insert path={
let \p1=($(#2)-(#1)$),\n1={veclen(\x1,\y1)/2} in ($(#1)!0.5!(#2)$) circle (\n1)}} 
}
\begin{document}

\begin{tikzpicture}[font=\sffamily,declare function={%
mangle(\a,\b,\c)=acos((\b/\c+\c/\b-(\a/\b)*(\a/\c))/2);}]
\pgfkeys{probe sphere radius/.store in=\ProbeSphereRadius,
probe sphere radius=1}
% define radii and center coordinates of the atoms
\edef\lstR{{0,1.7,1,1.8,1.8,1,1.7,1}}
\edef\lstCoords{(-4,1.5),(-1.2,2),(1.3,0.4),(4.5,0.1),(2.4,-2.3),(-2.3,-0.9),(-5.1,-1.4)}
% draw halo
\foreach \Coord [count=\Z] in \lstCoords
{\pgfmathsetmacro{\myR}{\lstR[\Z]+0.8}
\draw[dashed,thick] \Coord coordinate (c\Z) circle (\myR);}
\foreach \X/\Y in {1/2,1/6,1/7,2/6,2/3,3/4,3/5,3/6,4/5,6/7}
{\pgfmathsetmacro{\myRone}{\lstR[\X]+0.8}
\pgfmathsetmacro{\myRtwo}{\lstR[\Y]+0.8}
\fill[white,get circle intersections={c\X}{c\Y}{\myRone}{\myRtwo}{aux1}{aux2}]
 [midcircle=of aux1 and aux2];}
% draw atoms
\foreach \Coord [count=\Z] in \lstCoords
{\pgfmathsetmacro{\myR}{\lstR[\Z]}
\draw[green!40!black,thick] \Coord coordinate (c\Z) 
node{atom \Z} circle (\myR);}
% merge atoms
\foreach \X/\Y in {1/6,3/4}
{\pgfmathsetmacro{\myRone}{\lstR[\X]}
\pgfmathsetmacro{\myRtwo}{\lstR[\Y]}
\fill[white,get circle intersections={c\X}{c\Y}{\myRone}{\myRtwo}{aux1}{aux2}]
 [midcircle=of aux1 and aux2];}
\draw[red,thick]
  [merge circles={c1}{c2}{\lstR[1]}{\lstR[2]}] coordinate[pos=0](p0) coordinate[pos=1](p1)
  [merge circles={c2}{c3}{\lstR[2]}{\lstR[3]}] coordinate[pos=0](p2) coordinate[pos=1](p3)
  coordinate[pos=0.5](x1)
  [merge circles={c3}{c4}{\lstR[3]}{\lstR[4]}] coordinate[pos=0](p4) coordinate[pos=1](p5)
  [merge circles={c4}{c5}{\lstR[4]}{\lstR[5]}] coordinate[pos=0](p6) coordinate[pos=1](p7)
  [merge circles={c5}{c3}{\lstR[5]}{\lstR[3]}] coordinate[pos=0](p8) coordinate[pos=1](p9)
  [merge circles={c3}{c6}{\lstR[3]}{\lstR[6]}] coordinate[pos=0](p10) coordinate[pos=1](p11)
  [merge circles={c6}{c7}{\lstR[6]}{\lstR[7]}] coordinate[pos=0](p12) coordinate[pos=1](p13)
  [merge circles={c7}{c1}{\lstR[7]}{\lstR[1]}] coordinate[pos=0](p14) coordinate[pos=1](p15)
  ;
\draw[red,thick]
  [path along circle=with center c2 from p1 to p2,
 path along circle=with center c3 from p3 to p4,
 path along circle=with center c4 from p5 to p6,
 path along circle=with center c5 from p7 to p8,
 path along circle=with center c3 from p9 to p10,
 path along circle=with center c6 from p11 to p12,
 path along circle=with center c7 from p13 to p14,
 path along circle=with center c1 from p15 to p0];
\draw[thick,purple] let \p1=(intersection of c3--p4 and c4--p5)
                    in (\p1) coordinate (probe) circle (\ProbeSphereRadius);
\draw[latex-,thick,purple] ($(probe)+(60:\ProbeSphereRadius)$) 
-- ++ (1,0.3) node[right]{probe sphere};
\draw[latex-,dashed,thick] ($(c6)+(-60:\lstR[6]+0.8)$) -- ++(1,-1) 
node[below]{Solvent Accessible Surface};
\draw[latex-,thick,red] (x1) 
-- ++ (0,1.6) node[above]{Solvent Excluded Surface};
\draw[latex-,thick,green!40!black] ($(c5)+(45:\lstR[5])$) 
-- ++ (2.3,-0.9) node[below,align=center]{Van der Waals\\ surface};
\end{tikzpicture}
\end{document}

And if you replace the beginning by

\foreach \RR in {0.3,0.4,...,1.2,1.1,1.0,...,0.4}
{\begin{tikzpicture}[font=\sffamily,declare function={%
mangle(\a,\b,\c)=acos((\b/\c+\c/\b-(\a/\b)*(\a/\c))/2);}]
\pgfkeys{probe sphere radius/.store in=\ProbeSphereRadius,
probe sphere radius=\RR}
\path[use as bounding box] (-8,-5) rectangle (8,5);

and of course add } after \end{tikzpicture}, you see the impact of the probe sphere radius.

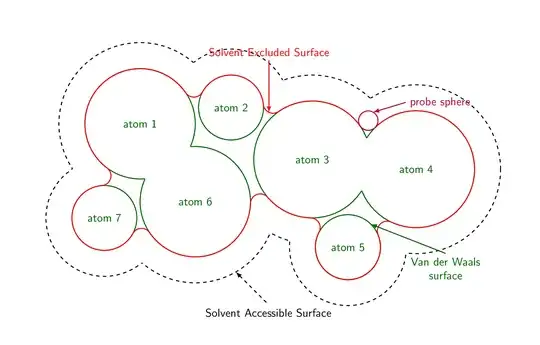
The following animation explains how that works.

\documentclass{beamer}
\beamertemplatenavigationsymbolsempty
\usepackage{tikz}
\usetikzlibrary{calc}
\tikzset{merge circles/.style n args={4}{insert path={
let \p1=(#1),\p2=(#2),\n1={veclen(\x1-\x2,\y1-\y2)*1pt/1cm},
\n2={atan2(\y2-\y1,\x2-\x1)},
\n3={mangle((#4+\ProbeSphereRadius),\n1,(#3+\ProbeSphereRadius))},
\n4={mangle(\n1,(#4+\ProbeSphereRadius),(#3+\ProbeSphereRadius))}
in %\pgfextra{\typeout{\n1,\n2,\n3,\n4}}
($(#1)+(+\n2+\n3:#3)$) arc(180+\n2+\n3:180+\n2+\n3+\n4:\ProbeSphereRadius)
}},
path along circle/.style args={with center #1 from #2 to #3}{insert path={
let \p1=($(#2)-(#1)$), \p2=($(#3)-(#1)$),
\n1={atan2(\y1,\x1)}, \n2={atan2(\y2,\x2)}, \n3={veclen(\x1,\y1)},
\n5={ifthenelse(\n2<\n1,\n2,\n2-360)}
in %\pgfextra{\typeout{\n1,\n2,\n5}}
 (#2) arc(\n1:\n5:\n3)}},
get circle intersections/.style n args={6}{insert path={
let \p1=(#1),\p2=(#2),\n1={veclen(\x1-\x2,\y1-\y2)*1pt/1cm},
\n2={atan2(\y2-\y1,\x2-\x1)},
\n3={mangle(#4,\n1,#3)},
\n4={mangle(\n1,#4,#3)}
in ($(#1)+(+\n2+\n3:#3)$) coordinate (#5) 
($(#1)+(+\n2-\n3:#3)$) coordinate (#6)}},
midcircle/.style args={of #1 and #2}{insert path={
let \p1=($(#2)-(#1)$),\n1={veclen(\x1,\y1)/2} in ($(#1)!0.5!(#2)$) circle (\n1)}} 
}
\begin{document}
\begin{frame}[t]
\frametitle{}
\centerline{\begin{tikzpicture}[scale=0.9,declare function={%
mangle(\a,\b,\c)=acos((\b/\c+\c/\b-(\a/\b)*(\a/\c))/2);}]
\pgfkeys{probe sphere radius/.store in=\ProbeSphereRadius,
probe sphere radius=1}
\draw (0,0) coordinate (c1) circle (3);
\draw (4,1) coordinate (c2) circle (2);
\draw (3,-2) coordinate (c3) circle (2);
\only<2->{\fill[white,get circle intersections={c1}{c2}{3}{2}{x1}{x2}]
[midcircle=of x1 and x2];
\fill[white,get circle intersections={c2}{c3}{2}{2}{x3}{x4}]
[midcircle=of x3 and x4];
\fill[white,get circle intersections={c3}{c1}{2}{3}{x5}{x6}]
[midcircle=of x5 and x6];
}
\only<3->{
\draw[red]
 [merge circles={c1}{c2}{3}{2}] coordinate[pos=0](p0) coordinate[pos=1](p1)
 [merge circles={c2}{c3}{2}{2}] coordinate[pos=0](p2) coordinate[pos=1](p3)
 [merge circles={c3}{c1}{2}{3}] coordinate[pos=0](p4) coordinate[pos=1](p5)
 [path along circle=with center c2 from p1 to p2,
path along circle=with center c3 from p3 to p4,
path along circle=with center c1 from p5 to p0];}
\end{tikzpicture}}
\begin{enumerate}
\item Draw the circles.
\item<2-> Wipe out the overlaps. \only<2>{First determine the coordinates at
which the circles intersect with \texttt{get circle intersections}
and then fill the midcircles with \texttt{midcircle}.}
\item<3-> Draw the arcs between the circles with \texttt{merge circles}
as well as the arcs along the circles with \texttt{path along circle}. 
\end{enumerate}
\end{frame}
\end{document}

ADDENDUM: Is that the area that should get shaded?

\documentclass[tikz,border=3.14mm]{standalone}
\usetikzlibrary{calc}
\tikzset{merge circles/.style n args={4}{insert path={
let \p1=(#1),\p2=(#2),\n1={veclen(\x1-\x2,\y1-\y2)*1pt/1cm},
\n2={atan2(\y2-\y1,\x2-\x1)},
\n3={mangle((#4+\ProbeSphereRadius),\n1,(#3+\ProbeSphereRadius))},
\n4={mangle(\n1,(#4+\ProbeSphereRadius),(#3+\ProbeSphereRadius))}
in %\pgfextra{\typeout{\n1,\n2,\n3,\n4}}
($(#1)+(+\n2+\n3:#3)$) arc(180+\n2+\n3:180+\n2+\n3+\n4:\ProbeSphereRadius)
}},
path along circle/.style args={with center #1 from #2 to #3}{insert path={
let \p1=($(#2)-(#1)$), \p2=($(#3)-(#1)$),
\n1={atan2(\y1,\x1)}, \n2={atan2(\y2,\x2)}, \n3={veclen(\x1,\y1)},
\n5={ifthenelse(\n2<\n1,\n2,\n2-360)}
in %\pgfextra{\typeout{\n1,\n2,\n5}}
 (#2) arc(\n1:\n5:\n3)}},
get circle intersections/.style n args={6}{insert path={
let \p1=(#1),\p2=(#2),\n1={veclen(\x1-\x2,\y1-\y2)*1pt/1cm},
\n2={atan2(\y2-\y1,\x2-\x1)},
\n3={mangle(#4,\n1,#3)},
\n4={mangle(\n1,#4,#3)}
in ($(#1)+(+\n2+\n3:#3)$) coordinate (#5) 
($(#1)+(+\n2-\n3:#3)$) coordinate (#6)}},
midcircle/.style args={of #1 and #2}{insert path={
let \p1=($(#2)-(#1)$),\n1={veclen(\x1,\y1)/2} in ($(#1)!0.5!(#2)$) circle (\n1)}} 
}
\begin{document}

\begin{tikzpicture}[font=\sffamily,declare function={%
mangle(\a,\b,\c)=acos((\b/\c+\c/\b-(\a/\b)*(\a/\c))/2);}]
\pgfkeys{probe sphere radius/.store in=\ProbeSphereRadius,
probe sphere radius=1}
% define radii and center coordinates of the atoms
\edef\lstR{{0,1.7,1,1.8,1.8,1,1.7,1}}
\edef\lstCoords{(-4,1.5),(-1.2,2),(1.3,0.4),(4.5,0.1),(2.4,-2.3),(-2.3,-0.9),(-5.1,-1.4)}
% draw halo
\foreach \Coord [count=\Z] in \lstCoords
{\pgfmathsetmacro{\myR}{\lstR[\Z]+0.8}
\draw[dashed,thick] \Coord coordinate (c\Z) circle (\myR);}
\foreach \X/\Y in {1/2,1/6,1/7,2/6,2/3,3/4,3/5,3/6,4/5,6/7}
{\pgfmathsetmacro{\myRone}{\lstR[\X]+0.8}
\pgfmathsetmacro{\myRtwo}{\lstR[\Y]+0.8}
\fill[white,get circle intersections={c\X}{c\Y}{\myRone}{\myRtwo}{aux1}{aux2}]
 [midcircle=of aux1 and aux2];}
\foreach \Coord [count=\Z] in \lstCoords
{\pgfmathsetmacro{\myR}{\lstR[\Z]+0.8}
\fill[cyan!20] \Coord coordinate (c\Z) circle (\myR);}
% draw atoms
\foreach \Coord [count=\Z] in \lstCoords
{\pgfmathsetmacro{\myR}{\lstR[\Z]}
\draw[green!40!black,thick,fill=white] \Coord coordinate (c\Z) 
node{atom \Z} circle (\myR);}
% merge atoms
\foreach \X/\Y in {1/6,3/4}
{\pgfmathsetmacro{\myRone}{\lstR[\X]}
\pgfmathsetmacro{\myRtwo}{\lstR[\Y]}
\fill[white,get circle intersections={c\X}{c\Y}{\myRone}{\myRtwo}{aux1}{aux2}]
 [midcircle=of aux1 and aux2];}
\draw[red,thick]
  [merge circles={c1}{c2}{\lstR[1]}{\lstR[2]}] coordinate[pos=0](p0) coordinate[pos=1](p1)
  [merge circles={c2}{c3}{\lstR[2]}{\lstR[3]}] coordinate[pos=0](p2) coordinate[pos=1](p3)
  coordinate[pos=0.5](x1)
  [merge circles={c3}{c4}{\lstR[3]}{\lstR[4]}] coordinate[pos=0](p4) coordinate[pos=1](p5)
  [merge circles={c4}{c5}{\lstR[4]}{\lstR[5]}] coordinate[pos=0](p6) coordinate[pos=1](p7)
  [merge circles={c5}{c3}{\lstR[5]}{\lstR[3]}] coordinate[pos=0](p8) coordinate[pos=1](p9)
  [merge circles={c3}{c6}{\lstR[3]}{\lstR[6]}] coordinate[pos=0](p10) coordinate[pos=1](p11)
  [merge circles={c6}{c7}{\lstR[6]}{\lstR[7]}] coordinate[pos=0](p12) coordinate[pos=1](p13)
  [merge circles={c7}{c1}{\lstR[7]}{\lstR[1]}] coordinate[pos=0](p14) coordinate[pos=1](p15)
  ;
\draw[red,thick]
  [path along circle=with center c2 from p1 to p2,
 path along circle=with center c3 from p3 to p4,
 path along circle=with center c4 from p5 to p6,
 path along circle=with center c5 from p7 to p8,
 path along circle=with center c3 from p9 to p10,
 path along circle=with center c6 from p11 to p12,
 path along circle=with center c7 from p13 to p14,
 path along circle=with center c1 from p15 to p0];
\draw[thick,purple] let \p1=(intersection of c3--p4 and c4--p5)
                    in (\p1) coordinate (probe) circle (\ProbeSphereRadius);
\draw[latex-,thick,purple] ($(probe)+(60:\ProbeSphereRadius)$) 
-- ++ (1,0.3) node[right]{probe sphere};
\draw[latex-,dashed,thick] ($(c6)+(-60:\lstR[6]+0.8)$) -- ++(1,-1) 
node[below]{Solvent Accessible Surface};
\draw[latex-,thick,red] (x1) 
-- ++ (0,1.6) node[above]{Solvent Excluded Surface};
\draw[latex-,thick,green!40!black] ($(c5)+(45:\lstR[5])$) 
-- ++ (2.3,-0.9) node[below,align=center]{Van der Waals\\ surface};
\end{tikzpicture}
\end{document}

On the first of your pictures, the center of the probe circle isn't on the dashed black line. This seems false. — quark67, Dec 07 '18 at 08:08
it is possible to fill the space between both surfaces with a color? — Kyle_the_hacker, Dec 07 '18 at 16:53
@quark67 Could we please swap roles? You write a complex answer, and I just state without reading it that it is wrong? (Don't get me wrong, it is certainly possible that I messed something up. But your comment is not too constructive, and, to be honest I do not know what to make of it. Either you make more effort in writing it, or please consider just getting rid of it.) — , Dec 08 '18 at 07:32
@marmot: I meant just the area between the solvent-excluded and the solvent-accessible surface — Kyle_the_hacker, Dec 08 '18 at 13:41
@marmot I'm sorry if my comment was considered too rude to you. English is not my natural language, I don't known too many words for precisely express my thoughts. I would just write about a possible omission in your code. I always admire your ability with Tikz, and your very hard effort to help others with generosity. Sorry if this comment is off topic. — quark67, Dec 09 '18 at 05:40

Solvent-accessible and -excluded surface

1 Answers1