TikZ-Roulette: Make animation more realistic

Question

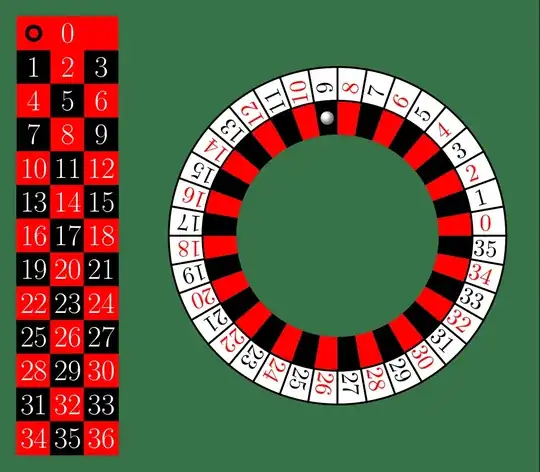
Consider the following MWE:

\documentclass[tikz]{standalone}
\usetikzlibrary{backgrounds}
\definecolor{filz}{RGB}{56,114,73}
%\pagecolor{filz}
\newcommand{\roulette}[1]{
%   \pgfmathsetseed{3}
    \pgfmathsetmacro\random{10*random(0,36)}
    \foreach \n in {0,10,...,\random}
%   \foreach \n in {\random,...,\random}
    {
        \begin{tikzpicture}
            \useasboundingbox (-.5,-.75) rectangle (3.5,2.75);

                \begin{scope}[scale=.25,shift={(-2,10)}]
                    \foreach \x in {1,...,3}
                    \foreach \y in {1,...,12}
                    {
                        \pgfmathsetmacro\number{int(\x+3*(\y-1))} 
                        \pgfmathsetmacro\testnumber{int(mod(\number,2))}

                        \ifnum\testnumber=0
                            \node[scale=.25,text=white,fill=red,minimum height=1.01cm,minimum width=1.01cm] at (\x,-\y) {\Huge\number};
                        \else
                            \node[scale=.25,text=white,fill,minimum height=1.01cm,minimum width=1.01cm] at (\x,-\y) {\Huge\number};
                        \fi
                    }

                    \node[scale=.25,text=white,fill=red,minimum height=1.01cm,minimum width=3.01cm] at (2,0) {\Huge 0};

                    \pgfmathsetmacro\testing{#1}
                    \pgfmathsetmacro\secure{int(mod(int(\testing),3))}

                    \ifnum\secure=0
                        \pgfmathsetmacro\xpos{mod(\testing,3)+3}
                        \pgfmathsetmacro\ypos{-int(\testing/3)}
                    \else
                        \pgfmathsetmacro\xpos{mod(\testing,3)}
                        \pgfmathsetmacro\ypos{-int(\testing/3)-1}
                    \fi

                    \ifnum#1>0
                    \pgfmathsetmacro\anothertest{int(mod(#1,2))}
                    \ifnum\anothertest=0
                        \draw[black,thick,fill=red] (\xpos,\ypos) circle(.2);
                    \else
                        \draw[red,thick,fill=black] (\xpos,\ypos) circle(.2);
                    \fi
                    \else
                        \draw[black,thick,fill=red] (1,0) circle(.2);
                    \fi
                \end{scope}

                \begin{scope}[shift={(2,1)}]
                    \foreach[count=\xx] \x in {0,20,...,340}
                    {
                        \fill[red] (\x:1) arc(\x:\x+10:1) -- (\x+10:.75) arc(\x+10:\x:.75) -- cycle;
                        \fill[rotate=10] (\x:1) arc(\x:\x+10:1) -- (\x+10:.75) arc(\x+10:\x:.75) -- cycle;
                            \draw[fill=white] (\x:1) arc(\x:\x+10:1) -- (\x+10:1.25) arc(\x+10:\x:1.25) -- cycle;
                            \draw[fill=white,rotate=10] (\x:1) arc(\x:\x+10:1) -- (\x+10:1.25) arc(\x+10:\x:1.25) -- cycle;
                    \pgfmathsetmacro\nn{int(2*(\xx-1))}
                        \pgfmathsetmacro\nnn{int(2*\xx-1)}
                            \node[red,rotate=\x,scale=.5] at (\x+5:1.1) {\nn};
                            \node[scale=.5,rotate=\x+15] at (\x+15:1.1) {\nnn};
                    }
                    \fill[ball color=white] (\n+5:{1-.05-(((1-2*.05)-.75)/2)}) circle(.05);
                \end{scope}

                \begin{pgfonlayer}{background}
                    \fill[filz] (current bounding box.south west) rectangle (current bounding box.north east);
                \end{pgfonlayer}
        \end{tikzpicture}
    }
}

\begin{document}
    \roulette{0}
\end{document}

Here is the output:

I know, that the numbers are not in the right order and that there is one number missing, but it's not important. My question is:

How can I achieve, that the roulette slice is rotating clockwise, while the ball is rotating counter-clockwise to the slice and that the both stop rotating, when the ball falls into a cell. The rotating should be just like in real life, i.e. the rotation is at the beginning faster than at the end.

I guess that this is more a question on the conversion (unless you are looking for an inline animation). Here you can read how one can compile to mp4. Whether or not it is possible to automatically change the speed of an mp4, I do not know, but you could afford many slides such that the effect can be achieved, which is probably hard with gifs which become really huge. — , Dec 26 '18 at 16:00

score 10 · Accepted Answer · answered Dec 26 '18 at 18:22

I followed a slightly different approach from @samcarter's and just assumed that the angular velocity decreases linearly from some maximal value vmax to zero. Then I integrated the angular velocity to get an angle. Sorry, I had to shorten your code a bit to produce a gif that can be uploaded. Unfortunately, I do not know how to upload mp4 files, which can be produced as described in this other answer by @samcarter.

\documentclass[tikz,border=3.14mm]{standalone}
\begin{document}
\pgfmathsetmacro{\Frame}{0}
\tikzset{declare function={tmax=100;
vmax=40;
rot(\t)=(\t/2)*(2-\t/tmax)*vmax;}}
\foreach \Frame in {0,...,100}
{\begin{tikzpicture}
\foreach \Y [evaluate=\Y as \X using {10*\Y+rot(\Frame)}] in {0,...,35}
{
\ifodd\Y
\fill (\X-5:2.5) -- (\X-5:2) arc(\X-5:\X+5:2) -- (\X+5:2.5) arc(\X+5:\X-5:2.5);
\node[rotate=\X] at (\X:2.75){\Y};
\else
\fill[red] (\X-5:2.5) -- (\X-5:2) arc(\X-5:\X+5:2) -- (\X+5:2.5) arc(\X+5:\X-5:2.5);
\node[rotate=\X,red] at (\X:2.75){\Y};
\fi
\draw (\X-5:2.5) -- (\X-5:3) arc(\X-5:\X+5:3) 
-- (\X+5:2.5) arc(\X+5:\X-5:2.5);
}
\shade[ball color=gray] ({-rot(\Frame)}:2.25) circle (1mm);
\end{tikzpicture}}
\end{document}

samcarter_is_at_topanswers.xyz · Answer 2 · 2018-12-26T18:08:48.347

For the part of your question about the slowing down:

A simple solution would be to write a wrapper document that displays each page of your animation an increasing number of times.

For example if your animation creates 16 pages, the following document will show the first page one time, the second page two times etc. You could also use other functions, this linear function is just an example:

\documentclass{beamer}

\setbeamertemplate{navigation symbols}{}
\usepackage{tikz}

\definecolor{filz}{RGB}{56,114,73}
\setbeamercolor{background canvas}{bg=filz}

\begin{document}

\foreach \n in {1,...,16}{

\begin{frame}[plain]
\foreach \x in {1,...,\insertframenumber}{
\includegraphics<+>[height=\paperheight,page=\insertframenumber]{document}}
\end{frame}

}

\end{document}

(sorry for the tiny image, the .gif would otherwise be too big to upload)

TikZ-Roulette: Make animation more realistic

2 Answers2