Yes, one can draw such things without caring about whether or nor some element is hidden. Personally like those things produced by these macros, these tricks and many other posts here much better. (If are saying that these should be parts of some packages by now, I would immediately agree, though.) UPDATE: Hide the hidden part of the longitude arc.
\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{tikz-3dplot}
\begin{document}
\tdplotsetmaincoords{105}{0}
\begin{tikzpicture}[tdplot_main_coords,font=\sffamily,line join=bevel]
\pgfmathsetmacro{\R}{3} % radius
\draw[thick,gray,dashed] (0,0,-\R-1) -- (0,0,\R+1);
\begin{scope}
\clip plot[variable=\x,domain=0:180] ({\R*cos(\x)},{\R*sin(\x)},0)
-- plot[variable=\x,domain=180:0,tdplot_screen_coords] ({\R*cos(\x)},{-\R*sin(\x)});
\shade[ball color=gray,opacity=0.2] [tdplot_screen_coords] (0,0) circle (\R);
\end{scope}
\draw[tdplot_screen_coords] (0,0) circle (\R);
% equator
\draw[fill=gray,opacity=0.15] plot[variable=\x,domain=0:360,smooth] ({\R*cos(\x)},{\R*sin(\x)},0);
% upper latitude circle
\pgfmathsetmacro{\Lat}{48}
\draw[fill=gray,opacity=0.15] plot[variable=\x,domain=0:360,smooth]
({\R*cos(\x)*sin(\Lat)},{\R*sin(\x)*sin(\Lat)},{\R*cos(\Lat)});
% longitude halfcircle with extensions
\pgfmathsetmacro{\Lon}{50}
\pgfmathsetmacro{\thetacrit}{atan(cos(\tdplotmaintheta)/(sin(\tdplotmaintheta)*sin(\Lon)))}
\draw[thick,gray] (0,0,-\R-1) -- (0,0,-\R)
plot[variable=\x,domain={180+\thetacrit}:0,smooth]
({\R*cos(\Lon)*sin(\x)},{\R*sin(\Lon)*sin(\x)},{\R*cos(\x)})
-- (0,0,\R+1) node[black,above left] {axis of rotation};
\draw[thick] ({\R*cos(\Lon)*sin(90)},{\R*sin(\Lon)*sin(90)},{\R*cos(90)})
-- (0,0,0) -- ({\R*cos(\Lon)*sin(\Lat)},{\R*sin(\Lon)*sin(\Lat)},{\R*cos(\Lat)})
coordinate (L);
\draw[thick,gray] plot[variable=\x,domain=90:\Lat,smooth]
({0.7*\R*cos(\Lon)*sin(\x)},{0.7*\R*sin(\Lon)*sin(\x)},{0.7*\R*cos(\x)});
\node [tdplot_screen_coords] at (1,0.4) {$\lambda$};
\draw[orange,tdplot_screen_coords] (L) to[out=0,in=180] ++ (2,1) node[right]{$\lambda=$latitude};
\draw[fill=blue] (L) circle (2pt);
\path (0,0,\R) coordinate (N) (0,0,-\R) coordinate (S) (-\R,0,0) coordinate (W)
({\R*cos(\Lon)*sin(135)},{\R*sin(\Lon)*sin(135)},{\R*cos(135)}) coordinate (M);
\draw[-latex,very thick,gray] plot[variable=\x,domain=150:30,smooth]
({cos(\x)*sin(\Lat)},{sin(\x)*sin(\Lat)},{\R+0.5});
\draw ([xshift=-2mm]W) -- ++ (-1,0) node[left]{equator}
(N) to[out=180,in=0] ++ (-2,0.2cm) node[left]{north pole}
(S) to[out=180,in=0] ++ (-2,-0.2cm) node[left]{south pole};
\draw[orange,tdplot_screen_coords] (M) -- ++ (0.2,-1) node[below]{meridian};
\end{tikzpicture}
\end{document}
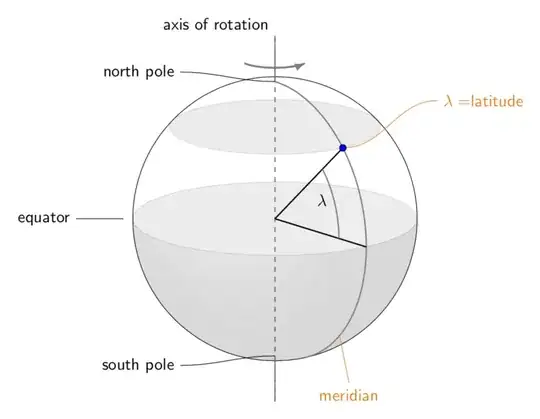


tikz-3dplot. – Jan 02 '19 at 23:30