How does TikZ parse powers?

Question

I was often stumbling upon (and correcting by hand) an IMHO rather surprising behavior of TikZ: powers are parsed in an unconventional way. Look at the MWE

\documentclass[tikz,border=3.14mm]{standalone}
\begin{document}
\begin{tikzpicture}
 \begin{scope}[local bounding box=symb]
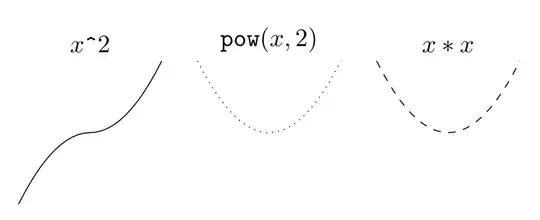
  \draw plot[variable=\x,domain=-1:1] (\x,{\x^2});
 \end{scope}
 \node[anchor=south] at (symb.north) {$x\verb|^|2$};
 % 
 \begin{scope}[xshift=2.5cm,local bounding box=pow]
 \draw[dotted] plot[variable=\x,domain=-1:1] (\x,{pow(\x,2)});
 \end{scope}
 \node[anchor=south] at (pow.north) {$\texttt{pow}(x,2)$};
 % 
 \begin{scope}[xshift=5cm,local bounding box=star]
 \draw[dashed] plot[variable=\x,domain=-1:1] (\x,{\x*\x});
 \end{scope}
 \node[anchor=south] at (star.north) {$x*x$};
\end{tikzpicture}
\end{document}

The left/solid plot shows x^2, and naively I would expect it to coincide with pow(x,2) and x*x, but it doesn't. Rather, for negative x, the plot also grows in the negative direction.

On the other hand, pgfplots seems to correct for this, even/also (but not only) when one uses declare function.

\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\begin{document}
\begin{tikzpicture}[declare function={f(\x)=\x^2;}]
 \begin{axis}[width=4cm,title={pgfplots}]
 \addplot[domain=-1:1] {f(x)};
 \end{axis}
 \begin{scope}[xshift=5cm,yshift=1cm,local bounding box=tikz]
 \draw plot[variable=\x,domain=-1:1] (\x,{f(\x)});
 \end{scope}
 \node[anchor=south] at (tikz.north) {Ti\emph{k}Z};
\end{tikzpicture}
\end{document}

Naively, I'd expect the plots having the same qualitative shape (modulo adjustments of length scales made by pgfplots, of course). So pgfplots and TikZ seem to interpret the same function differently.

Question: Why is that? Is there a simple way to make TikZ produce the expected output (i.e. x^2 is nonnegative)?

NOTE: @circumscribe made me aware of this earlier question. Apart from the comparison to pgfplots, this post does not add anything to the story, and in any case most likely the only viable answer is this one. So I will certainly not object to this question being closed as a duplicate of this earlier question. (I did search for earlier questions, but was under the impression they should contain parse in the title, which is why I didn't find it.)

@Zarko Sure. This is what I did in all my answers so far (where that mattered). — , Jan 11 '19 at 18:51
also work correctly if you enclose variable in parenthesis: f(\x)=(\x)^2. it seem that negative values of variable pgfplots and pure tikz treats differently — Zarko, Jan 11 '19 at 18:53
@Zarko Thanks! Yes. The thing is that pgfplots does not require these brackets, which is why added the comparison. (But you are right, I could or even should have added the bracket example as well. ) — , Jan 11 '19 at 18:54
That's really strange. In /usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathparser.code.tex it seems that \x^2 is the same as pow(\x,2) with very high precedence...: \pgfmathdeclareoperator{^}{pow} {2}{infix}{900} — Rmano, Jan 11 '19 at 19:14
@Rmano I guess that the sign does not get squared, i.e. the parser sets the brackets not in the way one may expect it to. — , Jan 11 '19 at 19:16
Yep. My guess of the problem is that when going through the function calculation, the value of \x is first substituted with the number and then parsed as a math expression, I mean: for \x=-1, plot first substitutes \x with -1, and then computes -1^2 which is, correctly, -1. The problem is that you should always surround values with parenthesis when substituting... That reminds me the classic problem with #define VAR -1 in C. — Rmano, Jan 11 '19 at 19:24
@Rmano I agree with all that. And this is what I did in many answers so far. My question is more whether there is a reason for that. Since pgfplots behaves differently, I guess that at least Christian Feuersänger noticed that and changed this. (I know of course that the pgfplots parser works a bit different, which is why you can use f(x) instead of f(\x). ) To me it is simply strange that \x^2 and pow(\x,2) are not equivalent. — , Jan 11 '19 at 19:27
So, for negative values, x^2 is computed as -|x|^2? arrrrhhh — Sigur, Jan 11 '19 at 19:53
@marmot may be TikZ took BODMAS very strictly than it should be ;) — Raaja_is_at_topanswers.xyz, Jan 12 '19 at 07:40
In any case, avoid all formats which allows floating point exponents, since they are implemented as exp(2*log(\x)). — John Kormylo, Jan 12 '19 at 15:45
@manooooh What I meant to say is that the parsing is unfortunate for all even powers, because the result of the parsing x^n is sign(x)*pow(abs(x),n), where n is the (integer) power. For odd n this is what one might expect, for even n it may be called unexpected. — , Jan 13 '19 at 03:42
@marmot: Have you seen the answers to this question? I have no idea if it's helpful or if the patch that's mentioned in the second answer (still) works. — Circumscribe, Jan 13 '19 at 22:51
@Circumscribe Thanks! I was not aware of this post. I guess that my post may be viewed as a duplicate. (The only thing my post may add is the comparison to pgfplots, which one may expect to behave the same as TikZ concerning the parsing of functions. Yet this is not a big deal.) — , Jan 13 '19 at 23:05
It's quite unfortunate, this mistake is hard to avoid because of how intuitive the syntax appears to be. Hendrik Vogt's patch seems to still work by the way, and it looks like what is does is precisely add (…) around the plot variable and {…} around the coordinates. Not sure how comfortable I'd feel using it though… — Circumscribe, Jan 14 '19 at 00:02
@Circumscribe Yes, this works as far as I can tell. I actually wrote several answers where I was either using this or \x*\x or pow(x,2). The reason why I brought this up was that the difference in behavior of TikZ and pgfplots, which keeps concerning me a bit. — , Jan 14 '19 at 02:50

How does TikZ parse powers?

0 Answers0

Linked