I am trying to draw a circle (sphere) passing through four points B, C, E, F like this picture
I tried with tikz-3dplot and my code
\documentclass[border=3mm,12pt]{standalone}
\usepackage{fouriernc}
\usepackage{tikz,tikz-3dplot}
\usepackage{tkz-euclide}
\usetkzobj{all}
\usetikzlibrary{intersections,calc,backgrounds}
\begin{document}
\tdplotsetmaincoords{70}{110}
%\tdplotsetmaincoords{80}{100}
\begin{tikzpicture}[tdplot_main_coords,scale=1.5]
\pgfmathsetmacro\a{3}
\pgfmathsetmacro\b{4}
\pgfmathsetmacro\h{5}
% definitions
\path
coordinate(A) at (0,0,0)
coordinate (B) at (\a,0,0)
coordinate (C) at (0,\b,0)
coordinate (S) at (0,0,\h)
coordinate (E) at ({\a*\h^2/(\a*\a + \h*\h)},0,{(\a*\a*\h)/(\a*\a + \h*\h)})
coordinate (F) at (0,{(\b*\h*\h)/(\b*\b + \h*\h)},{(\b*\b*\h)/(\b*\b + \h*\h)});
\draw[dashed,thick]
(A) -- (B) (A) -- (C) (A) -- (E) (S)--(A) (F)--(A);
\draw[thick]
(S) -- (B) -- (C) -- cycle;
\draw[thick]
(F) -- (B) (C)--(E) (F)--(E);
\tkzMarkRightAngle(S,E,A);
\tkzMarkRightAngle(S,F,A);
\foreach \point/\position in {A/below,B/left,C/below,S/above,E/left,F/above}
{
\fill (\point) circle (.8pt);
\node[\position=3pt] at (\point) {$\point$};
}
\end{tikzpicture}
\end{document}
and got
How can I draw a circle (sphere) passing through four points B, C, E, F?



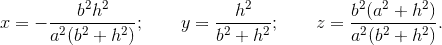

BC, notEC. I am trying your hint. – minhthien_2016 Jan 15 '19 at 04:35