Vertical sliced cylinder

Question

I want to explain how the shape of a cylinder is made. Therefore I want te make this picture.

My code is this:

\documentclass{article}

\usepackage{siunitx}
\usepackage{tkz-euclide}

\begin{document}

\begin{center}
\begin{tikzpicture}
\tkzInit[xmin=0,xmax=7,ymax=8]
\tkzClip
%\tkzGrid
\tkzDefPoints{3.5/1/A, 3.5/5/B} ;
\draw[thick] (A) ellipse (1.5 and 0.5);
\draw[thick] (B) ellipse (1.5 and 0.5);
\draw[thick] (2,1) -- (2,5);
\draw[thick] (5,1) -- (5,5);  
\draw[dashed,white,thick] (2,1) arc (180:360:1.5 and -0.5);
\tkzLabelSegment[below,sloped,yshift=2.2cm](A,B){h=\SI{6}{\cm}}; 
\end{tikzpicture}
\end{center}

\end{document}

Resulting in:

But I have a feeling that it is not a good start.

Any suggestions?

Milo · Accepted Answer · 2019-02-03T22:17:06.017

Here is one way to do it which adapts the code you were already using to draw the cylinders (i.e. using ellipses). This method uses the intersections library to calculate the intersection point of a line drawn radially out from the centre of the ellipse to the edge of the ellipse.

\documentclass[tikz,margin=0.5cm]{standalone}
\usetikzlibrary{intersections}

\begin{document}

\begin{tikzpicture}[thick,line join=bevel]

\useasboundingbox (1,0) rectangle (6,6);

\coordinate (A) at (3.5,1);
\coordinate (B) at (3.5,5);

\draw (2,1) -- (2,5);
\draw (5,1) -- (5,5);  
\path [name path=arcBabove] (2,5) arc (180:360:1.5 and -0.5);
\path [name path=arcBbelow] (2,5) arc (180:0:1.5 and -0.5);
\path [name path=arcAabove] (2,1) arc (180:360:1.5 and -0.5);
\path [name path=arcAbelow] (2,1) arc (180:0:1.5 and -0.5);

\draw [fill=orange,fill opacity=0.5] (A)--(2,1) node [midway,below,text opacity=1] {$r$} --(2,5)--(B);

\foreach \X in {40,20,10}{%
    \path[name path=line1] (A) -- ++(\X:3);
    \path[name intersections={of=arcAabove and line1,by={Int1}}] (A) -- (Int1);
    \path[name path=line2] (Int1) -- ++(90:10);
    \path[name intersections={of=arcBabove and line2,by={Int2}}] (Int1) -- (Int2);
    \draw [fill=white] (A)--(Int1)--(Int2)--(B)--(A);
    }

\foreach \X in {0,-11,-22.5,-40,-65}{%
    \path[name path=line1] (A) -- ++(\X:3);
    \path[name intersections={of=arcAbelow and line1,by={Int1}}] (A) -- (Int1);
    \path[name path=line2] (Int1) -- ++(90:10);
    \path[name intersections={of=arcBbelow and line2,by={Int2}}] (Int1) -- (Int2);
    \draw [fill=white] (A)--(Int1)--(Int2)--(B)--(A);
    }

\draw (2,5) arc (180:360:1.5 and -0.5);
\draw (2,5) arc (180:0:1.5 and -0.5);
\draw [dashed] (2,1) arc (180:360:1.5 and -0.5);
\draw (2,1) arc (180:0:1.5 and -0.5);

\end{tikzpicture}
\end{document}

With some shading to give a 3D effect

\documentclass[tikz,margin=0.5cm]{standalone}
\usetikzlibrary{intersections}

\begin{document}

\begin{tikzpicture}[thick,line join=bevel]

\useasboundingbox (1,0) rectangle (6,6);

\coordinate (A) at (3.5,1);
\coordinate (B) at (3.5,5);

\draw (2,1) -- (2,5);
\draw (5,1) -- (5,5);  
\path [name path=arcBabove] (2,5) arc (180:360:1.5 and -0.5);
\path [name path=arcBbelow] (2,5) arc (180:0:1.5 and -0.5);
\path [name path=arcAabove] (2,1) arc (180:360:1.5 and -0.5);
\path [name path=arcAbelow] (2,1) arc (180:0:1.5 and -0.5);

\draw [fill=orange,fill opacity=0.5] (A)--(2,1) node [midway,below, text opacity=1] {$r$}--(2,5)--(B);

\foreach \X in {40,20,10}{%
    \path[name path=line1] (A) -- ++(\X:3);
    \path[name intersections={of=arcAabove and line1,by={Int1}}] (A) -- (Int1);
    \path[name path=line2] (Int1) -- ++(90:10);
    \path[name intersections={of=arcBabove and line2,by={Int2}}] (Int1) -- (Int2);
    \draw [left color=black!70,right color=white] (A)--(Int1)--(Int2)--(B)--(A);
    }

\foreach \X in {0,-11,-22.5,-40,-65}{%
    \path[name path=line1] (A) -- ++(\X:3);
    \path[name intersections={of=arcAbelow and line1,by={Int1}}] (A) -- (Int1);
    \path[name path=line2] (Int1) -- ++(90:10);
    \path[name intersections={of=arcBbelow and line2,by={Int2}}] (Int1) -- (Int2);
    \draw [left color=black!70,right color=white] (A)--(Int1)--(Int2)--(B)--(A);
    }
    \draw [left color=black!20,right color=white] (A)--(Int1)--(Int2)--(B)--(A);

\draw (2,5) arc (180:360:1.5 and -0.5);
\draw (2,5) arc (180:0:1.5 and -0.5);
\draw [dashed] (2,1) arc (180:270:1.5 and -0.5);
\draw (2,1) arc (180:0:1.5 and -0.5);

\end{tikzpicture}
\end{document}

Just for fun, a cone and a ball shape:

Cone

\begin{tikzpicture}[thick,line join=bevel]

\useasboundingbox (1,0) rectangle (6,6);

\coordinate (A) at (3.5,1);
\coordinate (B) at (3.5,5);

\path [name path=arcAabove] (2,1) arc (180:360:1.5 and -0.5);
\path [name path=arcAbelow] (2,1) arc (180:0:1.5 and -0.5);

\draw [fill=orange,fill opacity=0.5] (A)--(2,1) node [midway,below, text opacity=1] {$r$}--(B);

\foreach \X in {0,-11,-22.5,-40,-65}{%
    \path[name path=line1] (A) -- ++(\X:3);
    \path[name intersections={of=arcAbelow and line1,by={Int1}}] (A) -- (Int1);
    \draw [left color=black!70,right color=white] (A)--(Int1)--(B)--(A);
}
\draw [left color=black!20,right color=white] (A)--(Int1)--(B)--(A);

\draw [dashed] (2,1) arc (180:270:1.5 and -0.5);
\draw (2,1) arc (180:0:1.5 and -0.5);

\end{tikzpicture}

Ball

Check out the answer by marmot for a more realistic ball!

\begin{tikzpicture}[thick,line join=bevel]

\useasboundingbox (1,0) rectangle (6,6);

\pgfmathsetmacro{\R}{1.5}

\coordinate (A) at (3.5,3);
\draw (A) circle (\R);
\draw [fill=orange,fill opacity=0.5] (A)--++(-90:\R) arc (270:90:\R) -- cycle;

\coordinate (B) at (3.5,3+\R);

\foreach \X in {1.5 ,1.35 ,1.1 ,0.8 ,0.4 }{%
    \draw [left color=black!70,right color=white] (B) arc (90:-90:\X and 1.5) -- cycle;
}
\draw [left color=black!30,right color=white] (B) arc (90:-90:0.4 and 1.5) -- cycle;

\draw [dashed] (2,3) arc (-180:0:1.5 and 0.3);
\draw [dashed] (2,3) arc (180:90:1.5 and 0.3);
\node (label) [inner sep=3pt]  at (3.5-\R/2,3) {$r$};
\draw (A)--(label.east) (label.west) --(2,3);

\end{tikzpicture}

Great! I'll try to understand your elegant code, so that I make it for a cone and a bol! — Arne Timperman, Feb 03 '19 at 14:46
@Milo I realized it for the cone... :D but 10^3 thanks for the code! And the ball (that I also needed!!!) — Arne Timperman, Feb 03 '19 at 17:13

score 5 · Answer 2 · 2019-02-05T15:18:24.623

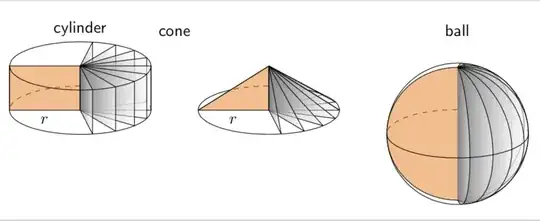
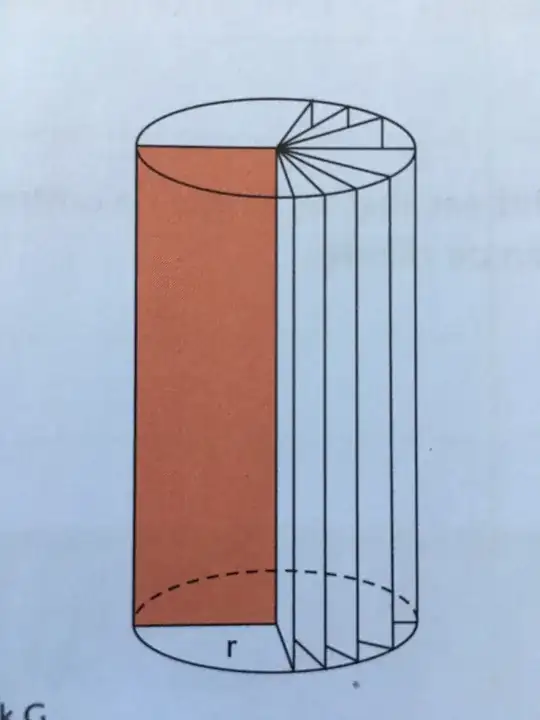
This is just for fun. I really like Milo's nice answer. The only minor issue I have is with the sphere. Either the dashed line is not the equator or the points at which the dividers intersect are not the poles. The following employs orthographic projections, and you can adjust the theta angle, i.e. the first argument of \tdplotsetmaincoords{70}{0}, at will. (EDIT: added line join=bevel, thanks to minhthien_2016!)

\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{tikz-3dplot} 
\begin{document}
\tdplotsetmaincoords{70}{0}
\begin{tikzpicture}[tdplot_main_coords,font=\sffamily,line join=bevel]
\pgfmathsetmacro{\r}{1.5}
\pgfmathsetmacro{\h}{3}
 \begin{scope}[local bounding box=cylinder]
  \draw[dashed] plot[smooth,variable=\t,domain=0:180] ({\r*cos(\t)},{\r*sin(\t)},0);
  \draw[fill=orange,fill opacity=0.5] (0,0) -- (-\r,0,0) 
   node[midway,below,opacity=1] {$r$}  -- (-\r,0,\h) --  (0,0,\h);
  \foreach \Z in {80,60,...,-80}
   {\draw[left color=gray,right color=white,fill opacity=0.5] (0,0,0) -- ({\r*cos(\Z)},{\r*sin(\Z)},0) -- 
    ({\r*cos(\Z)},{\r*sin(\Z)},\h) -- (0,0,\h) -- cycle;}
  \draw plot[smooth,variable=\t,domain=0:-180] ({\r*cos(\t)},{\r*sin(\t)},0)
   --  plot[smooth,variable=\t,domain=-180:180] ({\r*cos(\t)},{\r*sin(\t)},\h)
   (\r,0,0) -- (\r,0,\h);
 \end{scope}
 \node[anchor=south] at (cylinder.north) {cylinder};
 %
 \begin{scope}[local bounding box=cone,xshift={(2*\r+1)*1cm}]
  \draw[dashed] plot[smooth,variable=\t,domain=0:180] ({\r*cos(\t)},{\r*sin(\t)},0);
  \draw[fill=orange,fill opacity=0.5] (0,0) -- (-\r,0,0) 
  node[midway,below,opacity=1] {$r$}  -- (0,0,\h);
  \foreach \Z in {80,60,...,-80}
   {\draw[left color=gray,right color=white,fill opacity=0.5] (0,0,0) 
    -- ({\r*cos(\Z)},{\r*sin(\Z)},0) -- (0,0,\h) -- cycle;}
  \draw plot[smooth,variable=\t,domain=0:-180] ({\r*cos(\t)},{\r*sin(\t)},0)
   -- (0,0,\h) -- (\r,0,0) ;
 \end{scope}
 \node[anchor=south] at (cone.north|-cylinder.north) {cone};
 %
 \begin{scope}[local bounding box=ball,xshift={(2*\r+1)*2cm},yshift={(\h-\r)*1cm}]
  \draw[dashed] plot[smooth,variable=\t,domain=0:180] ({\r*cos(\t)},{\r*sin(\t)},0);
  \draw[fill=orange,fill opacity=0.5] 
   plot[smooth,variable=\t,domain=90:270] ({\r*cos(\t)},0,{\r*sin(\t)});
   \foreach \Z in {80,60,...,-80}
   {\draw[left color=gray,right color=white,fill opacity=0.5] 
    plot[smooth,variable=\t,domain=90:270]
    ({-\r*cos(\t)*cos(-\Z)},{\r*cos(\t)*sin(-\Z)},{\r*sin(\t)});}
  \draw[tdplot_screen_coords] (0,0) circle[radius=\r];
  \draw plot[smooth,variable=\t,domain=0:-180] 
   ({\r*cos(\t)},{\r*sin(\t)},0);  
 \end{scope}
 \node[anchor=south] at (ball.north|-cylinder.north) {ball};
 %
\end{tikzpicture}
\end{document}

And a version for minhthien_2016:

\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{tikz-3dplot}
% https://tex.stackexchange.com/a/12033/121799
\tikzset{reverseclip/.style={insert path={(current bounding box.north
        east) rectangle (current bounding box.south west)}}}
\begin{document}
\tdplotsetmaincoords{70}{0}
\begin{tikzpicture}[tdplot_main_coords,font=\sffamily,line join=bevel]
\pgfmathsetmacro{\r}{1.5}
\pgfmathsetmacro{\h}{1}
 \begin{scope}[local bounding box=cylinder]
  \draw[dashed] plot[smooth,variable=\t,domain=0:180] ({\r*cos(\t)},{\r*sin(\t)},0);
  \draw[fill=orange,fill opacity=0.5] (0,0) -- (-\r,0,0) 
   node[midway,below,opacity=1] {$r$}  -- (-\r,0,\h) --  (0,0,\h);
  \foreach \Z in {80,60,...,-80}
   {\draw[left color=gray,right color=white,fill opacity=0.5] (0,0,0) -- ({\r*cos(\Z)},{\r*sin(\Z)},0) -- 
    ({\r*cos(\Z)},{\r*sin(\Z)},\h) -- (0,0,\h) -- cycle;}
  \draw plot[smooth,variable=\t,domain=0:-180] ({\r*cos(\t)},{\r*sin(\t)},0)
   --  plot[smooth,variable=\t,domain=-180:180] ({\r*cos(\t)},{\r*sin(\t)},\h)
   (\r,0,0) -- (\r,0,\h);
 \end{scope}
 \node[anchor=south] at (cylinder.north) {cylinder};
 %
 \begin{scope}[local bounding box=cone,xshift={(2*\r+1)*1cm}]
  \begin{scope}
   \clip (-\r,0,0)  -- (0,0,\h) -- (\r,0,0) -- cycle; 
   \draw[dashed] plot[smooth,variable=\t,domain=0:180] ({\r*cos(\t)},{\r*sin(\t)},0);
  \end{scope}
  \draw[fill=orange,fill opacity=0.5] (0,0) -- (-\r,0,0) 
  node[midway,below,opacity=1] {$r$}  -- (0,0,\h);
  \foreach \Z in {80,60,...,-80}
   {\draw[left color=gray,right color=white,fill opacity=0.5] (0,0,0) 
    -- ({\r*cos(\Z)},{\r*sin(\Z)},0) -- (0,0,\h) -- cycle;}
  \begin{scope} 
   \clip (\r,0,0) -- (0,0,\h) -- (-\r,0,0) -- (\r,0,0) [reverseclip];
   \draw plot[smooth,variable=\t,domain=0:360] ({\r*cos(\t)},{\r*sin(\t)},0);    
  \end{scope}
  \draw (-\r,0,0)  -- (0,0,\h) -- (\r,0,0) ;
 \end{scope}
 \node[anchor=south] at (cone.north|-cylinder.north) {cone};
 %
 \begin{scope}[local bounding box=ball,xshift={(2*\r+1)*2cm},yshift={(\h-\r)*1cm}]
  \draw[dashed] plot[smooth,variable=\t,domain=0:180] ({\r*cos(\t)},{\r*sin(\t)},0);
  \draw[fill=orange,fill opacity=0.5] 
   plot[smooth,variable=\t,domain=90:270] ({\r*cos(\t)},0,{\r*sin(\t)});
   \foreach \Z in {80,60,...,-80}
   {\draw[left color=gray,right color=white,fill opacity=0.5] 
    plot[smooth,variable=\t,domain=90:270]
    ({-\r*cos(\t)*cos(-\Z)},{\r*cos(\t)*sin(-\Z)},{\r*sin(\t)});}
  \draw[tdplot_screen_coords] (0,0) circle[radius=\r];
  \draw plot[smooth,variable=\t,domain=0:-180] 
   ({\r*cos(\t)},{\r*sin(\t)},0);  
 \end{scope}
 \node[anchor=south] at (ball.north|-cylinder.north) {ball};
 %
\end{tikzpicture}
\end{document}

Please note line of base of the cone. I view it with 300%, it is not good. — minhthien_2016, Feb 04 '19 at 06:31
@minhthien_2016 Thanks! I added line join=bevel. (You might be interested in this very nice addition by Henri Menke. It will be uploaded at a given time, and I plan to use it for for the 3d intersections that without your help never were created, let alone created correctly.) — , Feb 04 '19 at 06:52
If I use your code in article class I had to ad \usepackage{tkz-euclide} . If not I got errors. Do you have the same experience? — Arne Timperman, Feb 04 '19 at 09:51
@ArneTimperman No, one definitely does not have to add \usepackage{tkz-euclide}. Note that tikz in \documentclass[tikz,border=3.14mm]{standalone} loads tikz. Did you load tikz? — , Feb 04 '19 at 14:41
@minhthien_2016 Yes, precisely. The idea is that you will no longer have to say \path[intersection of line trough={(0,0,0) and (\a,\b,\h) with plane containing (34/11, 34/11, 0) and normal (-5*\h, -2*\h, -28 + 5*\a + 2*\b)}] coordinate (H); but could use symbolic coordinates like \path[intersection of line trough={(A) and (C) with plane containing (B) and normal (N)}] coordinate (H);. — , Feb 04 '19 at 14:43
@marmot No I did not, but as I loaded the tkz-euclide it also loaded the tikz package. As you said, tikz is enough. — Arne Timperman, Feb 04 '19 at 16:06
@minhthien_2016 You only have to replace the dashed line by a solid one. — , Feb 05 '19 at 14:32
@minhthien_2016 I added a version here that only has the background path dashed. BTW, please avoid wordings like "base of cone very bad". First of all, some may feel it is offensive, and second it does not reveal what precisely you dislike. — , Feb 05 '19 at 15:19
@minhthien_2016 No worries! (I have just seen some comments derailing.) — , Feb 05 '19 at 15:39

Vertical sliced cylinder

2 Answers2

Cone

Ball