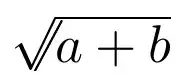Special square root for complex numbers?

Question

Our professor used a special looking square root for complex number notations, which I can't find. It looked like \sqrt was thrown into \mathbb (with a second diagonal line).

Detexify was no help and I can't find any other reference so far. I hope it wasn't his "invention".

Does anyone know, how I can produce such a special looking square root?

Edit: As requested, an image of it from my notes:

Till date I have not seen such a representation anywhere but here ;) however, it may be better to ask it here as well: https://math.stackexchange.com/ (such a thing might exist, I dont know) :D. — Raaja_is_at_topanswers.xyz, Feb 08 '19 at 10:12
Professors don't always realize that what they write on a blackboard, is not always possible using typesetting systems. — daleif, Feb 08 '19 at 10:42
One can do a hack to have what you want but in this case only. If you want to define the symbol generally, it is very hard and complicated, in my opinion. — , Feb 08 '19 at 11:02
In my opinion there is no need to introduce a special symbol for complex roots -- anyone familiar with complex numbers knows that roots can be calculated of complex numbers as well and that the easiest way is to apply the root to the polar coordinate version of those numbers. — , Feb 08 '19 at 11:14
@JouleV we can achieve it in Tikz by manipulating the bounding boxes per se. However, as much as it is a fun exercise, I'm not sure about it's applicability, collectively speaking. — Raaja_is_at_topanswers.xyz, Feb 08 '19 at 11:16
Don't know the use or appropriateness of the symbol, but maybe taken as a (La)TeX challenge rather than mathematical purity. In searching over TeX.SE I found an answer which does a bit of that (only the last overhang). Thought if the link could lead to the slant line too being included as a special square-root symbol. — Partha D., Feb 08 '19 at 11:40

Steven B. Segletes · Answer 1 · 2019-02-22T12:23:09.353

One could argue that this does not fit the OP's description, but since the symbol is non-standard, one can sort of have some flexibility in defining it.

\documentclass{article}
\usepackage{stackengine,mathtools}
\stackMath
\newcommand\ssqrt[2][\relax]{%
  \ifx\relax#1\relax%
    \stackengine{0pt}{\sqrt{\phantom{#2}}}{\mkern3mu\sqrt{#2}}{O}{c}{F}{F}{L}%
  \else%
    \stackengine{0pt}{\sqrt[#1]{\phantom{#2}}}{\mkern3mu\sqrt[\phantom{#1}]{#2}}{O}{c}{F}{F}{L}%    
  \fi%
}
\begin{document}
\[
  \ssqrt{z}\quad\ssqrt[n]{z}
\]

\[
  \ssqrt{\frac{x}{y}}\quad\ssqrt[3]{\frac{x}{y}}
\]
\end{document}

For something more sophisticated, certainly not perfect, and the dimensions of the macro dependent on the font and fontsize,

\documentclass{article}
\usepackage{stackengine,mathtools,trimclip,scalerel}
\stackMath
\newcommand\ssqrt[2][\relax]{\ThisStyle{%
  \ifx\relax#1\relax%
    \setbox0=\hbox{$\SavedStyle\sqrt{\phantom{\cramped{#2}}}$}%
    \def\tmpwd{\dimexpr2.5pt + .18\ht0\relax}% FONT DEPENDENT
    \stackengine{0pt}{%
      \SavedStyle\mkern1.5mu\sqrt{#2}%
    }{%
      \kern\tmpwd\clipbox{\tmpwd{} 2pt 0pt 0pt}{\copy0}%
    }{O}{l}{F}{F}{L}%
  \else%
    \setbox0=\hbox{$\SavedStyle\sqrt[\phantom{#1}]{\phantom{\cramped{#2}}}$}%
    \setbox2=\hbox{$\scriptscriptstyle#1$}%
    \def\tmpwd{\dimexpr+3.2pt +.5\wd2 + .08\ht0\relax}% FONT DEPENDENT
    \stackengine{0pt}{%
      \SavedStyle\mkern1.5mu\sqrt[#1]{#2}%
    }{%
      \kern\tmpwd\clipbox{\tmpwd{} 0pt 0pt 0pt}{\copy0}%
    }{O}{l}{F}{F}{L}%
  \fi%
}}
\begin{document}
\[
  \ssqrt{z}\quad\ssqrt[3]{z}\quad\ssqrt[n]{z^2 + 37}
\]
\[
  \ssqrt{\frac{x}{y}}\quad\ssqrt[3]{\frac{x}{y}}\quad\ssqrt[n]{\frac{x^2 + 37}{y}}
\]
\[\textstyle
  \ssqrt{z}\quad\ssqrt[3]{z}\quad\ssqrt[n]{z^2 + 37}
\]
\[\textstyle
  \ssqrt{\frac{x}{y}}\quad\ssqrt[3]{\frac{x}{y}}\quad\ssqrt[n]{\frac{x^2 + 37}{y}}
\]
\[\scriptstyle
  \ssqrt{z}\quad\ssqrt[3]{z}\quad\ssqrt[n]{z^2 + 37}
\]
\[\scriptstyle
  \ssqrt{\frac{x}{y}}\quad\ssqrt[3]{\frac{x}{y}}\quad\ssqrt[n]{\frac{x^2 + 37}{y}}
\]
\end{document}

Great! I'am very happy to see another solution. – Sebastiano Feb 22 '19 at 16:46 — Sebastiano, Feb 22 '19 at 16:46

score 2 · Answer 2 · edited Feb 22 '19 at 12:25

For fun: A first try with @marmot's nice answer:

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{tikzmark,calc}
\newcounter{stuff}
%https://tex.stackexchange.com/questions/461193/floating-point-square-root-symbol
\tikzset{toughtoroot/.style={path picture={\draw
            let \p1=($(path picture bounding box.north west)-(path picture bounding box.south west)$) in ($(path picture bounding box.south west)+(0.4em, -0.1em)$)
            -- ($(path picture bounding box.north)-({0.25em+\x1/10},0)-(0.3em, 0.1em)$);}}}
\begin{document}
$\tikzmarknode[toughtoroot]{1}{\sqrt{a+b}}$
\end{document}

this will give you

Disclaimer: This is far from a mature solution. Work in progress ;-). Note that this only works for this case and not a generalistic one (yet!).

Sebastiano · Answer 3 · 2019-02-22T20:39:10.420

1

I have not used a particular and complicate code. I have added a backslash near the \sqrt.

Here there is the output (more perfect than first my answer):

\documentclass[12pt]{article}
\usepackage{graphicx,amssymb,scalerel}
\begin{document}
\[ \sqrt[n]{{\rotatebox{-4}{  $\mkern-14mu \mathrel{\stretchto{/}{2ex}}$  }}\mkern-6mu z} \]
\end{document}

edited Feb 22 '19 at 20:39

answered Feb 22 '19 at 09:04

Sebastiano

54,118

Special square root for complex numbers?

3 Answers3