Using functions like sine, cosine and tangent to calculate coordinates in Tikz

Question

I am learning TikZ with the pgfmanual. The example given is as follows:

I have achieved the following so far:

The code is as follows:

\documentclass{article}
\usepackage{tikz}

\tikzset{help lines/.style=very thin}
\tikzset{My Grid/.style={help lines,color=blue!50}}

\begin{document}
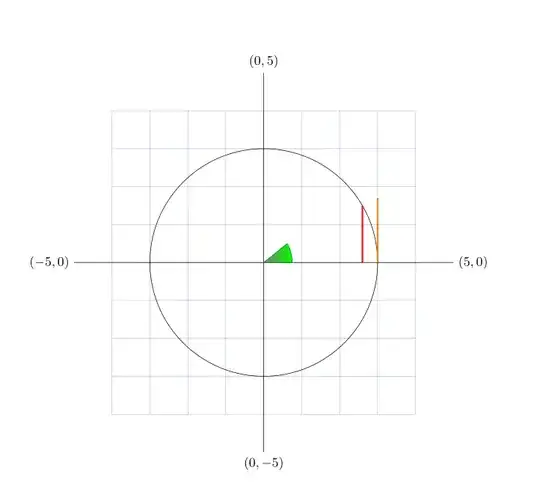
\begin{tikzpicture}
  \draw[My Grid] (-4,-4) grid (4,4);
  \draw (-5,0) node[left] {$(-5,0)$} -- (5,0) node[right] {$(5,0)$};
  \draw (0,-5) node[below] {$(0,-5)$} -- (0,5) node[above] {$(0,5)$};
  \draw (0,0)  circle [radius=3cm];
  \shadedraw[left color=gray, right color=green, draw=green!50!black] (0,0) -- (0.75,0)  arc [start angle=0, end angle=30, radius=1cm] -- cycle;
  \draw[red, very thick] (30:3cm) -- (2.6,0);
  \draw [very thick,orange] (3,0) -- (3,1.7);
\end{tikzpicture}
\end{document}

To achieve the intersection of the slope and tangent, pgfmanual uses the concept of path and intersections library which is very confusing.

Is there an easier way to tell the system to draw a line from point A to sin(30) as point B and to draw tangent of the angle proportionately instead of using direct numbers.

Please suggest alternative apart from intersections, polar coordinates and paths. Because the pgfmanual already uses them which is hard to understand.

May be If you specify exactly what is hard for you to understand someone will try to explain it to you — Hafid Boukhoulda, Feb 23 '19 at 08:14
@hafid The slope lines and connecting the tangent for the time being — subham soni, Feb 23 '19 at 08:16
Do you need to use cos(30) and tan(30) to indicate point coordinates instead of (2.6,0) and (3,1.7) — Hafid Boukhoulda, Feb 23 '19 at 08:23
I think your approach is simpler than working with explicit sin and cos functions. E.g. the red line can be drawn like \draw[red, very thick] (30:3cm) -- (0,0-|30:3cm);, where the last coordinate is the projection of the first one on y=0. — , Feb 23 '19 at 14:11

Hafid Boukhoulda · Answer 1 · 2019-02-23T10:54:47.157

14

Since in cos(30) and tan(30) there are parentheses you must put these functions inside curly brackets {}

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{angles,quotes}

\tikzset{help lines/.style=very thin}
\tikzset{My Grid/.style={help lines,color=blue!50}}

\begin{document}
\begin{tikzpicture}
  \draw[My Grid] (-4,-4) grid (4,4);
  \draw (-5,0) node[left] {$(-5,0)$} -- (5,0) node[right] {$(5,0)$};
  \draw (0,-5) node[below] {$(0,-5)$} -- (0,5) node[above] {$(0,5)$};
  \draw (0,0)  circle [radius=3cm];

%   \shadedraw[left color=gray, right color=green, draw=green!50!black]
% (0,0) -- (0.75,0)  arc [start angle=0, end angle=30, radius=0.75cm] --  cycle;

  \coordinate(O)at(0,0);
  \draw[red, very thick] (30:3cm)coordinate(A) 
                         --({3*cos(30)},0)coordinate(B);

  \draw [very thick,orange] (3,0) -- (3,{3*tan(30)})coordinate(C);

  \pic[fill=green!50!black,
       angle radius=0.75cm,
       angle eccentricity=1.2,
       "\(\alpha\)"] {angle=B--O--A};

   \draw (O)--(C);

\end{tikzpicture}
\end{document}

edited Feb 23 '19 at 10:54

answered Feb 23 '19 at 08:27

Hafid Boukhoulda

8,563

Will this ensure that the length is actual value when computed as well or plotted manually with pencil and graph? – subham soni Feb 23 '19 at 08:32
@subhamsoni I notice that the green angle is greeter than 30° I suppose you needed to be 30° – Hafid Boukhoulda Feb 23 '19 at 08:38
I have mentioned end angle as 30. Is there anything I am missing – subham soni Feb 23 '19 at 08:39
@subhamsoni Yes you need the specify the correct radius 0.75 cm and not 1cm since the start point is (0.75,0). Also in Tikz there is another manner to draw angles. – Hafid Boukhoulda Feb 23 '19 at 08:43
it would be great if you can share the other way because precision is always better. – subham soni Feb 23 '19 at 08:46
Also how is the radius determined. How did you compute 0.75 – subham soni Feb 23 '19 at 08:46
@subhamsoni Since the arc start point is (0.75,0) and the center of the arc is (0,0) so the radius must be 0.75. If not you will get an arc with a different center. I have updated my answer to show an alternative manner to draw angles. – Hafid Boukhoulda Feb 23 '19 at 09:14
The slope and the tangent must stop at intersection. How do we do that. It should not extend beyond point of intersection. – subham soni Feb 23 '19 at 10:48
@subhamsoni Answer updated – Hafid Boukhoulda Feb 23 '19 at 10:57

score 3 · Answer 2 · 2019-02-23T15:23:49.317

Here is an alternative to Hafid's nice answer, going further into the direction you started. You do not need to use any trigonometric function. Just using polar coordinates and projections is sufficient.

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{calc,angles,quotes}
\tikzset{help lines/.style=very thin}
\tikzset{My Grid/.style={help lines,color=blue!50}}

\begin{document}
\begin{tikzpicture}
  \draw[My Grid] (-4,-4) grid (4,4);
  \draw (-5,0) node[left] {$(-5,0)$} -- (5,0) node[right] {$(5,0)$};
  \draw (0,-5) node[below] {$(0,-5)$} -- (0,5) node[above] {$(0,5)$};
  \draw (0,0) coordinate (O)  circle [radius=3cm];
  \draw[red, very thick] (30:3cm) coordinate (A) 
  % (30:3cm) is a polar coordinate with angle 30 (degrees) and radius 3cm
  -- (0,0-|A) coordinate(Ax)
  %  (0,0-|30:3cm) is a point that has the x coordinate of A and y=0
  % see https://tex.stackexchange.com/a/401429/121799 for more details
  node[midway,left]{$\sin\alpha$};
  \draw [very thick,orange] (3,0) -- (intersection cs:
  first line={(O)--(A)},second line={(3,0)--(3,3)}) coordinate(A')
  % (A') is at the intersections of the lines OA and the vertical line through (3,0)
  node[midway,right]{$\tan\alpha$};
  \pic[fill=green!50,angle radius=1cm,
       angle eccentricity=0.6, "$\alpha$"] {angle=Ax--O--A};
  % that's almost a 1-1 copy of what you can find on p. 560 of the manual      
  \draw (O) -- (A');
  \draw[very thick,blue] (O) -- (Ax) node[midway,below]{$\cos\alpha$};
\end{tikzpicture}
\end{document}

Thanks marmot . Can you please add comments to each line of the tikz code which will help me understand better. Especially the relationship between polar coordinates and projection — subham soni, Feb 23 '19 at 15:12
@subhamsoni I added explanations in the comments in the code. — , Feb 23 '19 at 15:24

Using functions like sine, cosine and tangent to calculate coordinates in Tikz

2 Answers2