Easiest way to interpolate increasingly closely in a diagram? [Regression, Curve Fitting]

Question

I am trying to create a diagram which looks like this:

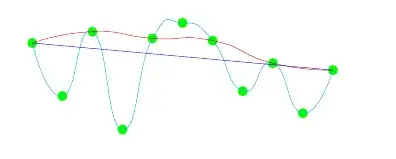
I have tried fitting a function with increasingly many nodes, but it does not look right (showing all 3 curves on the diagram to better illustrate):

\documentclass[10pt,landscape,a4paper]{article}
\usepackage[utf8]{inputenc}
\usepackage[UKenglish]{babel}
\usepackage{tikz}

\begin{document}

\begin{tikzpicture} [scale = 0.5]

\foreach \p in {-5,...,5} \node[circle,fill=green] at (\p,2*rand)  (\p) {};
\draw [cyan, xshift=4cm] plot [smooth, tension=1] coordinates { (-5) (-4) (-3) (-2) (-1) (0) (1) (2) (3) (4) (5) };
\draw [red, xshift=4cm] plot [smooth, tension=1] coordinates { (-5)  (-3)  (-1)  (1)  (3)  (5) };
\draw [blue, xshift=4cm] plot [smooth, tension=1] coordinates { (-5)  (5)  };
\end{tikzpicture}

\end{document}

I have also tried creating nodes like this (ie with a defined function x^2+x+1 + "noise" instead:

\foreach \p in {-5,...,5} \node[circle,fill=green] at (\p, \p * \p + \p + 1 + rand) (\p) {};

but that does not work at all.

In any case my code forces me to list nodes manually, which is not great.

I guess I need a way of interpolating with increasingly higher degree polynomials ? But I am not sure how to do this.

Answer 1

You could defined "interpolating" coordinates and connect those with a smooth plot.

\documentclass[10pt,landscape,a4paper]{article}
\usepackage{tikz}
\begin{document}

\begin{tikzpicture} [scale = 0.5]
\pgfmathtruncatemacro{\imin}{-5}
\pgfmathtruncatemacro{\imax}{5}
\foreach \p in {\imin,...,\imax} \node[circle,fill=green] at (\p,2*rand)  (p\p) {};
\foreach \X [evaluate=\X as \Xm using {int(\X-1)},evaluate=\X as \Xp using
{int(\X+1)}] in {\imin,...,\imax}
{\ifnum\X=\imin
  \path (p\X) coordinate (i\X);
 \else
  \ifnum\X=\imax
   \path (p\X) coordinate (i\X);
  \else
   \path (barycentric cs:p\X=0.6,p\Xm=0.2,p\Xp=0.2) coordinate (i\X);
  \fi 
 \fi
}
\draw [blue] plot [smooth, tension=1,variable=\X,samples at={\imin,...,\imax}] 
(i\X);
\end{tikzpicture}
\end{document}

Of course, you could change the weighting in addition to the tension.

\documentclass[tikz,border=3.14mm]{standalone}
\begin{document}
\foreach \X in {1,1.5,...,10,9.5,9,...,1.5}
{\begin{tikzpicture}
\pgfmathtruncatemacro{\imin}{-5}
\pgfmathtruncatemacro{\imax}{5}
\pgfmathsetmacro{\mainweight}{\X}
\pgfmathsetseed{27}
\node[anchor=north west,font=\sffamily] at (\imin,-2)
{weight is \pgfmathprintnumber{\mainweight}};
\foreach \p in {\imin,...,\imax} \node[circle,fill=green] at (\p,2*rand)  (p\p) {};
\foreach \X [evaluate=\X as \Xm using {int(\X-1)},evaluate=\X as \Xp using
{int(\X+1)}] in {\imin,...,\imax}
{\ifnum\X=\imin
  \path (p\X) coordinate (i\X);
 \else
  \ifnum\X=\imax
   \path (p\X) coordinate (i\X);
  \else
   \path (barycentric cs:p\X=\mainweight,p\Xm=1,p\Xp=1) coordinate (i\X);
  \fi 
 \fi
}
\draw [blue] plot [smooth, tension=0.5,variable=\X,samples at={\imin,...,\imax}] 
(i\X);
\end{tikzpicture}}
\end{document}