How do I make the characters have the same size?

Question

Th following is the full code that produces the image shown below:

\documentclass{article}
\usepackage[utf8]{inputenc}
\usepackage[english]{babel}

\usepackage{amsthm}
\usepackage{amsmath}
\usepackage[left=1.5in, right=1.5in, top=0.5in]{geometry}


\newtheorem{definition}{Definition}
\newtheorem{theorem}{Theorem} 
\theoremstyle{remark}

\begin{document}
    \title{Extra Credit}
    \maketitle

    \begin{definition}
        If f is analytic at $z_0$, then the series

        \begin{equation}
            f(z_0) + f'(z_0)(z-z_0) + \frac{f''(z_0)}{2!}(z-z_0)^2 + \cdots = \sum_{n=0}^{\infty} \frac{f^{(n)}(z_0)}{n!}(z-z_0)^n
        \end{equation}

        is called the Taylor series for f around $z_0$.
    \end{definition}

    \begin{theorem}
        If f is analytic inside and on the simple closed positively oriented contour $\Gamma$ and if $z_0$ is any point inside $\Gamma$, then
        \begin{equation}
            f^{(n)}(z_0) = \frac{n!}{2\pi i} \int_{\Gamma} \frac{f(\zeta)}{(\zeta - z_0)^{n+1}}d\zeta \hspace{1cm} (n=1,2,3, \cdots )
        \end{equation}
    \end{theorem}
    \hrulefill



\begin{theorem}
If f is analytic in the disk $|z-z_0|<R'$, then the Taylor series $(1)$ converges to $f(z)$ for all $z$ in this disk. 
\end{theorem}

\begin{proof}
Suppose that the function \textit{f} is analytic in the disk $|z-z_0|<R'$. We can define a positively oriented contour $C$ as $$ C:=\Big\{z:|z-z_0|=\frac{R + R'}{2}, 0<R< R'  \Big\}.$$ Letting $\zeta$ be an arbitrary point on $C$ and applying Theorem 1 to $(1)$, we get 

\begin{equation}
\sum_{n=0}^{\infty} \frac{(z-z_0)^{n}}{2\pi i} \int_{C} \frac{f(\zeta)}{(\zeta - z_0)^{n+1}}d\zeta.
\end{equation}\\ 

Or equivalently, we have that


\begin{align*}
  \sum_{n=0}^{\infty} \frac{(z-z_0)^{n}}{2\pi i} \int_{C} \frac{f(\zeta)}{(\zeta - z_0)^{n+1}}d\zeta
  &= \frac{1}{2\pi i} \sum_{n=0}^{\infty} \int_{C} \frac{(z-z_0)^{n}f(\zeta)}{(\zeta - z_0)^{n+1}}d\zeta 
  \\ &= \frac{1}{2\pi i}\int_{C}\sum_{n=0}^{\infty} \frac{1}{\zeta - z_0}\frac{f(\zeta)}{\frac{(\zeta - z_0)^n}{(z-z_0)^n}}d\zeta                   
  \\ &= \frac{1}{2\pi i} \int_{C} \frac{f(\zeta)}{\zeta - z_0}\sum_{n=0}^{\infty}\left( \frac{z-z_0}{\zeta - z_0}\right)^{n} d\zeta
\                   
\end{align*}

The above image is created using

\begin{align*}
  \sum_{n=0}^{\infty} \frac{(z-z_0)^{n}}{2\pi i} \int_{C} \frac{f(\zeta)}{(\zeta - z_0)^{n+1}}d\zeta
  &= \frac{1}{2\pi i} \sum_{n=0}^{\infty} \int_{C} \frac{(z-z_0)^{n}f(\zeta)}{(\zeta - z_0)^{n+1}}d\zeta 
  \\ &= \frac{1}{2\pi i}\int_{C}\sum_{n=0}^{\infty} \frac{1}{\zeta - z_0}\frac{f(\zeta)}{\frac{(\zeta - z_0)^n}{(z-z_0)^n}}d\zeta                   
  \\ &= \frac{1}{2\pi i} \int_{C} \frac{f(\zeta)}{\zeta - z_0}\sum_{n=0}^{\infty}\left( \frac{z-z_0}{\zeta - z_0}\right)^{n} d\zeta
\                   
\end{align*}

which is extracted from the full code above. How can I resize the second line of the image, so that all the characters are the same size?

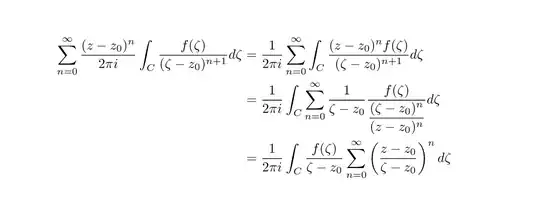
Use \displaystyle at the beginning of the outer denominator. — L. F., Mar 31 '19 at 05:49
Some general typesetting issues: (a) Don't write \textif{f}; do write $f$ . (b) Don't create paragraph breaks immediately before \begin{equation}, \begin{align*}, etc. Don't use\cdots; instead, write\dotsand let LaTeX (and theamsmathpackage) decide which kind of typographic ellipsis to insert. (d) Either insert\noindentbefore\hrulefillor, more simply, write\hrule`. — Mico, Mar 31 '19 at 06:08
I was wondering why we insert \noindent before \hrulefill? — Skm, Apr 01 '19 at 03:12

Przemysław Scherwentke · Answer 1 · 2019-03-31T06:10:17.300

You want to

\begin{align*}
  \sum_{n=0}^{\infty} \frac{(z-z_0)^{n}}{2\pi i} \int_{C} \frac{f(\zeta)}{(\zeta - z_0)^{n+1}}d\zeta
  &= \frac{1}{2\pi i} \sum_{n=0}^{\infty} \int_{C} \frac{(z-z_0)^{n}f(\zeta)}{(\zeta - z_0)^{n+1}}d\zeta 
  \\ 
&= \frac{1}{2\pi i}\int_{C}\sum_{n=0}^{\infty} \frac{1}{\zeta - z_0}\frac{f(\zeta)}{\displaystyle\frac{(\zeta - z_0)^n}{(z-z_0)^n}}d\zeta                   
  \\ &= \frac{1}{2\pi i} \int_{C} \frac{f(\zeta)}{\zeta - z_0}\sum_{n=0}^{\infty}\left( \frac{z-z_0}{\zeta - z_0}\right)^{n} d\zeta                  
\end{align*}

or simply \dfrac as you can use amsmath package.

Please observe also that one backslash before \end{align*} was removed.

How do I make the characters have the same size?

1 Answers1