I am often use coordinates of points to draw figure in geometry. I know that, we can add, minus coordinates of points, example
\begin{tikzpicture}
\tkzDefPoints{0/0/C',3/0/D',1/1/B'}
\coordinate (A') at ($(B')+(D')-(C')$);
\end{tikzpicture}
If I have two points A(1,2,3) and B(4,5,6), how can I define vector AB as (\B)-(\A)?
If you use the coordinates only for drawing, simply define each components of points as variable and then define coordinate points using them. For example:
\documentclass[margin=3.14159mm]{standalone}
\usepackage{tikz,tikz-3dplot}
\begin{document}
\tdplotsetmaincoords{60}{125}
\begin{tikzpicture}
[scale=0.9,
tdplot_main_coords,
axis/.style={-latex,thick},
vector/.style={-stealth,red,very thick},
vector guide/.style={dashed,thick}]
%standard tikz coordinate definition using x, y, z coords
% A(2,4,3), B(3,-1,4)
\def\Ax{2}
\def\Ay{4}
\def\Az{3}
\def\Bx{-1}
\def\By{3}
\def\Bz{4}
\coordinate (O) at (0,0,0);
\coordinate (A) at (\Ax,\Ay,\Az);
\coordinate (B) at (\Bx,\By,\Bz);
%draw axes
\draw[axis] (0,0,0) -- (4,0,0) node[anchor=north east]{$x$};
\draw[axis] (0,0,0) -- (0,4,0) node[anchor=north west]{$y$};
\draw[axis] (0,0,0) -- (0,0,5) node[anchor=south]{$z$};
%Dot at point
\fill [blue] (A) circle (2pt);
\fill [blue] (B) circle (2pt);
%draw a vector from O to A and O to B
\draw[vector guide] (O)node[left=1mm]{} -- (A)node[above=-1mm,right]{$P_1(\Ax,\Ay,\Az)$};
\draw[vector guide] (O) -- (B)node[above=-1mm,right]{$P_2(\Bx,\By,\Bz)$};
%draw vector D=AB
\draw[vector] (A) -- (B)node[midway,above,sloped]{$\mathbf{D}$};
\end{tikzpicture}
\end{document}
SUPPLEMENT
With the permission of the answerer, I (Steven B Segletes) show here how the listofitems package can be used to streamline the syntax and maybe provide more readability. With it, I can create the arrays by reading a list, with the syntax \readlist\A{2,4,3}. Then, the expression \A[] will spit back the array 2,4,3, which is sufficient for use in the present MWE. However, the individual components are also accessible as \A[1], \A[2], and \A[3], which can be used for various calculations, as required.
\documentclass[margin=3.14159mm]{standalone}
\usepackage{tikz,tikz-3dplot,listofitems}
\begin{document}
\tdplotsetmaincoords{60}{125}
\begin{tikzpicture}
[scale=0.9,
tdplot_main_coords,
axis/.style={-latex,thick},
vector/.style={-stealth,red,very thick},
vector guide/.style={dashed,thick}]
%standard tikz coordinate definition using x, y, z coords
% A(2,4,3), B(3,-1,4)
\readlist\A{2,4,3}
\readlist\B{-1,3,4}
\coordinate (O) at (0,0,0);
\coordinate (A) at (\A[]);
\coordinate (B) at (\B[]);
%draw axes
\draw[axis] (0,0,0) -- (4,0,0) node[anchor=north east]{$x$};
\draw[axis] (0,0,0) -- (0,4,0) node[anchor=north west]{$y$};
\draw[axis] (0,0,0) -- (0,0,5) node[anchor=south]{$z$};
%Dot at point
\fill [blue] (A) circle (2pt);
\fill [blue] (B) circle (2pt);
%draw a vector from O to A and O to B
\draw[vector guide] (O)node[left=1mm]{} -- (A)node[above=-1mm,right]{$P_1(\A[])$};
\draw[vector guide] (O) -- (B)node[above=-1mm,right]{$P_2(\B[])$};
%draw vector D=AB
\draw[vector] (A) -- (B)node[midway,above,sloped]{$\mathbf{D}$};
\end{tikzpicture}
\end{document}
listofitems package. Thank you very much.
–
Apr 01 '19 at 10:28
listofitems for your benefit. It is a very useful and versatile package.
– Steven B. Segletes
Apr 01 '19 at 10:45
Just for fun, I wrote routines for 3D vector addition, subtraction, cross product and dot product (scalar treated as a 1D vector). I was trying to actually parse expressions of the form \A+\B but eventually gave up.
\documentclass{article}
\usepackage{listofitems}
\usepackage{pgfmath}
\usepackage{amsmath}
\makeatletter
\newcommand{@vecargs}{}% reserve global names
\newcommand{\vecadd}{}
\newcommand{\vecsub}{}
\newcommand{\vecdot}{}
\newcommand{\veccross}{}
\newcommand{\vecparse}{}
\def\vecadd#1#2#3% #1 = #2 + #3
{\bgroup% local definitions
\pgfmathsetmacro{@x}{#2[1]+#3[1]}%
\pgfmathsetmacro{@y}{#2[2]+#3[2]}%
\pgfmathsetmacro{@z}{#2[3]+#3[3]}%
\xdef@vecargs{@x,@y,@z}%
\egroup
\readlist#1{@vecargs}}
\def\vecsub#1#2#3% #1 = #2 - #3
{\bgroup% local definitions
\pgfmathsetmacro{@x}{#2[1]-#3[1]}%
\pgfmathsetmacro{@y}{#2[2]-#3[2]}%
\pgfmathsetmacro{@z}{#2[3]-#3[3]}%
\xdef@vecargs{@x,@y,@z}%
\egroup
\readlist#1{@vecargs}}
\def\vecdot#1#2#3% #1 = #2 \cdot #3
{\pgfmathsetmacro{@vecargs}{#2[1]#3[1] + #2[2]#3[2] + #2[3]*#3[3]}%
\readlist#1{@vecargs}}
\def\veccross#1#2#3% #1 = #2 \times #3
{\bgroup% local definitions
\pgfmathsetmacro{@x}{#2[2]#3[3] - #2[3]#3[2]}%
\pgfmathsetmacro{@y}{#2[3]#3[1] - #2[1]#3[3]}%
\pgfmathsetmacro{@z}{#2[1]#3[2] - #2[2]#3[1]}%
\xdef@vecargs{@x,@y,@z}%
\egroup
\readlist#1{@vecargs}}
\makeatother
\begin{document}
\readlist\A{1,2,3}
\readlist\B{4,5,6}
\vecadd\C\A\B
\C[]
\vecsub\C\A\B
\C[]
\vecdot\C\A\B
\C[]
\veccross\C\A\B
\C[]
\end{document}
SUPPLEMENT
I hope John doesn't mind me (Steven B Segletes) adding his sought-after parser to the code. This allows input of the form \vecparse\C{\A+\B}, \vecparse\C{\A - \B}, \vecparse\C{\A .\B}, and \vecparse\C{\A x\B} (extra spaces of no consequence).
Support added not only for \vecparse\C{\A x\B}, but also \vecparse\C{\A x(3,5,6)}, \vecparse\C{(3,5,6)x\B} and \vecparse\C{(1,1,1)x(1,2,3)}.
\documentclass{article}
\usepackage{listofitems}
\usepackage{pgfmath}
\usepackage{amsmath}
\makeatletter
\newcommand{@vecargs}{}% reserve global names
\newcommand{\vecadd}{}
\newcommand{\vecsub}{}
\newcommand{\vecdot}{}
\newcommand{\veccross}{}
\newcommand{\vecparse}{}
\def\vecadd#1#2#3% #1 = #2 + #3
{\bgroup% local definitions
\pgfmathsetmacro{@x}{#2[1]+#3[1]}%
\pgfmathsetmacro{@y}{#2[2]+#3[2]}%
\pgfmathsetmacro{@z}{#2[3]+#3[3]}%
\xdef@vecargs{@x,@y,@z}%
\egroup
\setsepchar{,}%
\readlist#1{@vecargs}}
\def\vecsub#1#2#3% #1 = #2 - #3
{\bgroup% local definitions
\pgfmathsetmacro{@x}{#2[1]-#3[1]}%
\pgfmathsetmacro{@y}{#2[2]-#3[2]}%
\pgfmathsetmacro{@z}{#2[3]-#3[3]}%
\xdef@vecargs{@x,@y,@z}%
\egroup
\setsepchar{,}%
\readlist#1{@vecargs}}
\def\vecdot#1#2#3% #1 = #2 \cdot #3
{\pgfmathsetmacro{@vecargs}{#2[1]#3[1] + #2[2]#3[2] + #2[3]*#3[3]}%
\setsepchar{,}%
\readlist#1{@vecargs}}
\def\veccross#1#2#3% #1 = #2 \times #3
{\bgroup% local definitions
\pgfmathsetmacro{@x}{#2[2]#3[3] - #2[3]#3[2]}%
\pgfmathsetmacro{@y}{#2[3]#3[1] - #2[1]#3[3]}%
\pgfmathsetmacro{@z}{#2[1]#3[2] - #2[2]#3[1]}%
\xdef@vecargs{@x,@y,@z}%
\egroup
\setsepchar{,}%
\readlist#1{@vecargs}}
\def\vecparse#1#2{%
\setsepchar{+||-||x||./(||)}%
\readlist*@findop{#2}%
\ifnum\listlen@findop[1]=1\relax
\itemtomacro@findop[1]\tmpA
\else
\itemtomacro@findop[1,2]\tmpF
\setsepchar{,}%
\readlist\tmpE{\tmpF}%
\def\tmpA{\tmpE}%
\fi
\ifnum\listlen@findop[2]=1\relax
\itemtomacro@findop[2]\tmpB
\else
\itemtomacro@findop[2,2]\tmpD
\setsepchar{,}%
\readlist\tmpC{\tmpD}%
\def\tmpB{\tmpC}%
\fi
\if+@findopsep[1]\relax
\def\tmp{\vecadd#1}%
\else\if-@findopsep[1]\relax
\def\tmp{\vecsub#1}%
\else\if.@findopsep[1]\relax
\def\tmp{\vecdot#1}%
\else\if x@findopsep[1]\relax
\def\tmp{\veccross#1}%
\fi\fi\fi\fi
\expandafter\expandafter\expandafter\tmp\expandafter\tmpA\tmpB
}
\makeatother
\begin{document}
\readlist\A{1,2,3}
\readlist\B{4,5,6}
\vecadd\C\A\B
\C[]
VP:\vecparse\C{\A+\B}
\C[]
\vecsub\C\A\B
\C[]
VP:\vecparse\C{\A - \B}
\C[]
\vecdot\C\A\B
\C[]
VP:\vecparse\C{\A .\B}
\C[]
\veccross\C\A\B
\C[]
VP:\vecparse\C{\A x\B}
\C[]
VP:\vecparse\C{\A x(3,5,6)}
\C[]
VP:\vecparse\C{(3,5,6)x\B}
\C[]
VP:\vecparse\C{(1,1,1)x(1,2,3)}
\C[]
\end{document}
\edef\A{1,2,3} and only using lists to parse them.
– John Kormylo
Apr 02 '19 at 13:17
listofitems has a provided macro, \itemtomacro that might help in that regard, for extracting parts of or the whole of a list. I probably should have used it to assign \tmpA and \tmpB. ... I just did.
– Steven B. Segletes
Apr 02 '19 at 13:27
\A+(4,5,6) which are a lot easier when \A expands to 1,2,3 directly.
– John Kormylo
Apr 02 '19 at 13:34
\veccross definition for \@z. But I also took care of the parsing issue allowing for raw vector input.
– Steven B. Segletes
Apr 02 '19 at 14:44
\vecparse{\C=\A - \B} or \vecparse{\D=\C x (\A - \B)} or even \vecparse{D=C x (A - B)}? (The TikZ library math allows one to do some of these things for 2D vectors.)
–
Apr 02 '19 at 15:48
\vecdot:
#2[1]*#3[1] + #2[2]*#3[2] + #3[3]*#3[3]}
The final component of the dot product uses component 3 of vector B twice, rather than using components 3 from both vector A and vector B. So the code should read:
#2[1]*#3[1] + #2[2]*#3[2] + #2[3]*#3[3]}
It turns out that a commit by Henri Menke allows one to retrieve the raw coordinates of a symbolic coordinate: there is a command \coord that can be used with the calc library which provides the raw input coordinates. Then it is easy to add some functions that parse these.
\documentclass[tikz]{standalone}
\usetikzlibrary{calc}
\pgfmathdeclarefunction{xcomp3}{3}{% x component of a 3-vector
\begingroup%
\pgfmathparse{#1}%
\pgfmathsmuggle\pgfmathresult\endgroup}
\pgfmathdeclarefunction{ycomp3}{3}{% y component of a 3-vector
\begingroup%
\pgfmathparse{#2}%
\pgfmathsmuggle\pgfmathresult\endgroup}
\pgfmathdeclarefunction{zcomp3}{3}{% z component of a 3-vector
\begingroup%
\pgfmathparse{#3}%
\pgfmathsmuggle\pgfmathresult\endgroup}
\pgfmathdeclarefunction{veclen3}{3}{% 3d vector length
\begingroup%
\pgfmathparse{sqrt(pow(#1,2)+pow(#2,2)+pow(#3,2))}%
\pgfmathsmuggle\pgfmathresult\endgroup}
\newcommand{\spaux}[6]{(#1)*(#4)+(#2)*(#5)+(#3)*(#6)}
\pgfmathdeclarefunction{scalarproduct}{2}{% scalar product of two 3-vectors
\begingroup%
\pgfmathparse{\spaux#1#2}%
\pgfmathsmuggle\pgfmathresult\endgroup}
\newcommand{\vpauxx}[6]{(#2)*(#6)-(#3)*(#5)}
\newcommand{\vpauxy}[6]{(#4)*(#3)-(#1)*(#6)}
\newcommand{\vpauxz}[6]{(#1)*(#5)-(#2)*(#4)}
\pgfmathdeclarefunction{vpx}{2}{% x component of vector product
\begingroup%
\pgfmathparse{\vpauxx#1#2}%
\pgfmathsmuggle\pgfmathresult\endgroup}
\pgfmathdeclarefunction{vpy}{2}{% y component of vector product
\begingroup%
\pgfmathparse{\vpauxy#1#2}%
\pgfmathsmuggle\pgfmathresult\endgroup}
\pgfmathdeclarefunction{vpz}{2}{% z component of vector product
\begingroup%
\pgfmathparse{\vpauxz#1#2}%
\pgfmathsmuggle\pgfmathresult\endgroup}
\newcommand{\VP}[2]{% macro for vector product (not a function)
\pgfmathsetmacro\myx{vpx({#1},{#2})}%
\pgfmathsetmacro\myz{vpy({#1},{#2})}%
\pgfmathsetmacro\myy{vpz({#1},{#2})}%
(\myx,\myy,\myz)}
\begin{document}
\begin{tikzpicture}
\path (1,2,3) coordinate (a) (5,6,7) coordinate (b);
\path let \p1=(a),\p2=(b) in (0,-1)
node{$(a)=\coord1,(b)=\coord2,
\pgfmathsetmacro\myx{xcomp3\coord1}a_x=\myx,
\pgfmathsetmacro\myz{zcomp3\coord2}b_z=\myz,
\pgfmathsetmacro\myd{scalarproduct({\coord1},{\coord2})}
\vec a\cdot\vec b=\myd,%
\pgfmathsetmacro\myvpx{vpx({\coord1},{\coord2})}
\pgfmathsetmacro\myvpz{vpy({\coord1},{\coord2})}
\pgfmathsetmacro\myvpy{vpz({\coord1},{\coord2})}
\vec a\times\vec b=(\myvpx,\myvpy,\myvpz)=\VP{\coord1}{\coord2}
$};
\end{tikzpicture}
\end{document}
As long as you work in one frame, this allows you to parse all these things in a simple way. The raw coordinates do, however, not remember in which frame they are defined. (Note that there are also the commands \rawx, \rawy and \rawz, whose purpose is described here and here. They are not to be confused with the three entries of \coord in case one has declared them in 3d.)
NOTE: Some further developments of this can be found here. They allow you to build linear combinations and compute vector products of symbolic coordinates in 3d.
n and the point a, the equation will be \vec n\cdot (\vec a-\vec r)=0.
–
Aug 20 '19 at 07:03
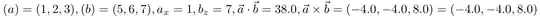
(1,2,3)is just fancy interface for a 2d point (that is a projection of this 3d point). – Kpym Apr 01 '19 at 09:30