How to draw toroidal grid diagrams in TikZ

Question

I am trying to turn a planar grid diagram into a 3D toroidal graph by identifying the top edge with the bottom and the left with the right, i.e:

So the grid below on the left would be transformed into a right-hand trefoil knot on a torus:

I would like to draw a torus which looks like this but with the grid structure (including the grid itself, the o's, the x's, and the red lines). Could I please have some help. Many thanks in advance!

Edit: I have created a 'torus' out of A4 for illustration - would like the x's and o's to be placed in certain unit grids and the red lines to be straight like in the original grid diagram:

Like in https://tex.stackexchange.com/questions/348/how-to-draw-a-torus ? — John Kormylo, Apr 25 '19 at 22:53
Most of it is not too difficult to achieve but the 3d shading of blue thing that wraps around it is comparatively tough. — , Apr 26 '19 at 00:56

score 4 · Accepted Answer · 2019-04-27T06:13:01.537

UPDATE: The quadrant problem is resolved and one can now draw the visible (or hidden) stretches only. All you need to do is to define a function of the torus coordinates u and v, and pgfplots can be used to draw only the visible parts.

\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\tikzset{declare function={torusx(\u,\v,\R,\r)=cos(\u)*(\R + \r*cos(\v)); 
torusy(\u,\v,\R,\r)=(\R + \r*cos(\v))*sin(\u);
torusz(\u,\v,\R,\r)=\r*sin(\v);
vcrit1(\u,\th)=atan(tan(\th)*sin(\u));% first critical v value
vcrit2(\u,\th)=180+atan(tan(\th)*sin(\u));% second critical v value
vtest(\u,\v,\az,\el)=sin(-vcrit1(\u-\az,\el)+\v);
disc(\th,\R,\r)=((pow(\r,2)-pow(\R,2))*pow(cot(\th),2)+% 
pow(\r,2)*(2+pow(tan(\th),2)))/pow(\R,2);% discriminant
umax(\th,\R,\r)=ifthenelse(disc(\th,\R,\r)>0,asin(sqrt(abs(disc(\th,\R,\r)))),0);
}}
\pgfplotsset{%
visible stretch/.style={restrict expr to domain={vtest(atan2(rawy,rawx),%
ifthenelse(veclen(rawx,rawy)>\R,asin(rawz/\r),180-asin(rawz/\r)),\pgfkeysvalueof{/pgfplots/view/az},\pgfkeysvalueof{/pgfplots/view/el})}{-0.05:1.1}},
hidden stretch/.style={restrict expr to domain={vtest(atan2(rawy,rawx),%
ifthenelse(veclen(rawx,rawy)>\R,asin(rawz/\r),180-asin(rawz/\r)),\pgfkeysvalueof{/pgfplots/view/az},\pgfkeysvalueof{/pgfplots/view/el})}{-1.1:0.05}}}
\begin{document}
\begin{tikzpicture}
\pgfmathsetmacro{\R}{4}
\pgfmathsetmacro{\r}{1}
\begin{axis}[colormap/blackwhite,
   view={40}{60},axis lines=none]
%\typeout{el=\pgfkeysvalueof{/pgfplots/view/el},az=\pgfkeysvalueof{/pgfplots/view/az}}     
\tikzset{declare function={%
myu(\t)=ifthenelse(\t<108,36,ifthenelse(\t<324,\t-72,ifthenelse(\t<432,252,\t-180)));
myv(\t)=ifthenelse(\t<108,\t,ifthenelse(\t<324,108,ifthenelse(\t<432,\t-216,216)));}}
%   \addplot3[very thick,red,samples y=0,domain=0:576,smooth,samples=46,hidden stretch
%   ]  
%         ({torusx(myu(x),myv(x),\R,\r)}, 
%         {torusy(myu(x),myv(x),\R,\r)}, 
%         {torusz(myu(x),myv(x),\R,\r)});

       \addplot3[surf,shader=interp,
       samples=61, point meta=z+sin(2*y),
       %surf,shader=flat,
       domain=0:360,y domain=0:360,
       z buffer=sort]
       ({torusx(x,y,\R,\r)}, 
        {torusy(x,y,\R,\r)}, 
        {torusz(x,y,\R,\r)});
    \pgfplotsinvokeforeach{0,30,...,330}  
    {\addplot3[samples y=0,domain=0:360,smooth,samples=71,visible stretch]  
        ({torusx(x,#1,\R,\r)}, 
        {torusy(x,#1,\R,\r)}, 
        {torusz(x,#1,\R,\r)});}

    \pgfplotsinvokeforeach{0,30,...,330}  
    {\addplot3[samples y=0,domain=0:360,smooth,samples=71,visible stretch]  
        ({torusx(#1,x,\R,\r)}, 
        {torusy(#1,x,\R,\r)}, 
        {torusz(#1,x,\R,\r)});}

    \addplot3[very thick,red,samples y=0,domain=0:576,smooth,samples=46,visible stretch]  
        ({torusx(myu(x),myv(x),\R,\r)}, 
        {torusy(myu(x),myv(x),\R,\r)}, 
        {torusz(myu(x),myv(x),\R,\r)});
\end{axis}
\end{tikzpicture}
\end{document}

Or

\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\tikzset{declare function={torusx(\u,\v,\R,\r)=cos(\u)*(\R + \r*cos(\v)); 
torusy(\u,\v,\R,\r)=(\R + \r*cos(\v))*sin(\u);
torusz(\u,\v,\R,\r)=\r*sin(\v);
vcrit1(\u,\th)=atan(tan(\th)*sin(\u));% first critical v value
vcrit2(\u,\th)=180+atan(tan(\th)*sin(\u));% second critical v value
vtest(\u,\v,\az,\el)=sin(-vcrit1(\u-\az,\el)+\v);
disc(\th,\R,\r)=((pow(\r,2)-pow(\R,2))*pow(cot(\th),2)+% 
pow(\r,2)*(2+pow(tan(\th),2)))/pow(\R,2);% discriminant
umax(\th,\R,\r)=ifthenelse(disc(\th,\R,\r)>0,asin(sqrt(abs(disc(\th,\R,\r)))),0);
}}
\pgfplotsset{%
visible stretch/.style={restrict expr to domain={vtest(atan2(rawy,rawx),%
ifthenelse(veclen(rawx,rawy)>\R,asin(rawz/\r),180-asin(rawz/\r)),\pgfkeysvalueof{/pgfplots/view/az},\pgfkeysvalueof{/pgfplots/view/el})}{-0.05:1.1}},
hidden stretch/.style={restrict expr to domain={vtest(atan2(rawy,rawx),%
ifthenelse(veclen(rawx,rawy)>\R,asin(rawz/\r),180-asin(rawz/\r)),\pgfkeysvalueof{/pgfplots/view/az},\pgfkeysvalueof{/pgfplots/view/el})}{-1.1:0.05}}}
\begin{document}
\begin{tikzpicture}
\pgfmathsetmacro{\R}{4}
\pgfmathsetmacro{\r}{1}
\begin{axis}[colormap/blackwhite,
   view={40}{60},axis lines=none]
%\typeout{el=\pgfkeysvalueof{/pgfplots/view/el},az=\pgfkeysvalueof{/pgfplots/view/az}}     
\tikzset{declare function={%
myu(\t)=\t;
myv(\t)=3*\t;}}
    \addplot3[very thick,gray,samples y=0,domain=0:576,smooth,samples=101]  
        ({torusx(myu(x),myv(x),\R,\r)}, 
        {torusy(myu(x),myv(x),\R,\r)}, 
        {torusz(myu(x),myv(x),\R,\r)});

       \addplot3[surf,shader=interp,opacity=0.8,
       samples=61, point meta=z+sin(2*y),
       %surf,shader=flat,
       domain=0:360,y domain=0:360,
       z buffer=sort]
       ({torusx(x,y,\R,\r)}, 
        {torusy(x,y,\R,\r)}, 
        {torusz(x,y,\R,\r)});
    \pgfplotsinvokeforeach{0,30,...,330}  
    {\addplot3[samples y=0,domain=0:360,smooth,samples=71,visible stretch]  
        ({torusx(x,#1,\R,\r)}, 
        {torusy(x,#1,\R,\r)}, 
        {torusz(x,#1,\R,\r)});}

    \pgfplotsinvokeforeach{0,30,...,330}  
    {\addplot3[samples y=0,domain=0:360,smooth,samples=71,visible stretch]  
        ({torusx(#1,x,\R,\r)}, 
        {torusy(#1,x,\R,\r)}, 
        {torusz(#1,x,\R,\r)});}

    \addplot3[very thick,red,samples y=0,domain=0:576,smooth,samples=101,visible stretch]  
        ({torusx(myu(x),myv(x),\R,\r)}, 
        {torusy(myu(x),myv(x),\R,\r)}, 
        {torusz(myu(x),myv(x),\R,\r)});
\end{axis}
\end{tikzpicture}
\end{document}

Original.

\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{tikz-3dplot}
\tikzset{declare function={%
torusx(\u,\v,\R,\r)=cos(\u)*(\R + \r*cos(\v)); 
torusy(\u,\v,\R,\r)=(\R + \r*cos(\v))*sin(\u);
torusz(\u,\v,\R,\r)=\r*sin(\v);
vcrit1(\u,\th)=atan(tan(\th)*sin(\u));% first critical v value
vcrit2(\u,\th)=180+atan(tan(\th)*sin(\u));% second critical v value
thetacritA(\R,\r)=atan(sqrt(\R/\r-1));
thetacritB(\R,\r)=acos(\r/\R);
ucritA(\R,\r,\th)=180+(90/pi)*sqrt(abs(-(\R^2*pow(cot(\th),2))+4*pow(\r,2)/pow(sin(2*\th),2)))/\R; 
ucritB(\R,\r,\th)=540-ucritA(\R,\r,\th);
umaxA(\R,\r,\th)=asin(sqrt(abs(-pow(cot(\th),2)+4*pow(\r,2)/(pow((sin(2*\th)*\R),2)))));
umaxB(\R,\r,\th)=180-umaxA(\R,\r,\th);}}
\begin{document} 
\tdplotsetmaincoords{65}{0}
\begin{tikzpicture}[tdplot_main_coords]
     \pgfmathsetmacro{\RadiusA}{3}
     \pgfmathsetmacro{\RadiusB}{1}
     \pgfmathsetmacro{\rprime}{1.25}
     % all v curves
     \foreach \X in {0,10,...,350}
     {\draw
        plot[variable=\x,domain=0:360,smooth]
    ({torusx(\X,\x,\RadiusA,\RadiusB)},{torusy(\X,\x,\RadiusA,\RadiusB)},{torusz(\X,\x,\RadiusA,\RadiusB)});
     }
     % all u curves
     \foreach \X in {0,30,...,330}
     {\draw plot[variable=\x,domain=0:360,smooth]
        ({torusx(\x,\X,\RadiusA,\RadiusB)},{torusy(\x,\X,\RadiusA,\RadiusB)},{torusz(\x,\X,\RadiusA,\RadiusB)});
     }
  \end{tikzpicture}
\end{document}

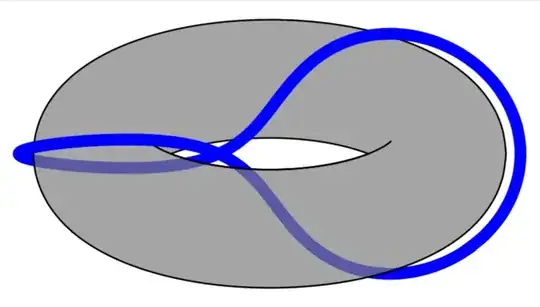
They can be used to discern hidden from visible stretches of something wrapping the torus, as illustrated in this answer where the functions are explained. In case you find it to cumbersome to patch things together you way want to consider switching to asymptote.

\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{tikz-3dplot}
\tikzset{declare function={%
torusx(\u,\v,\R,\r)=cos(\u)*(\R + \r*cos(\v)); 
torusy(\u,\v,\R,\r)=(\R + \r*cos(\v))*sin(\u);
torusz(\u,\v,\R,\r)=\r*sin(\v);
vcrit1(\u,\th)=atan(tan(\th)*sin(\u));% first critical v value
vcrit2(\u,\th)=180+atan(tan(\th)*sin(\u));% second critical v value
thetacritA(\R,\r)=atan(sqrt(\R/\r-1));
thetacritB(\R,\r)=acos(\r/\R);
ucritA(\R,\r,\th)=180+(90/pi)*sqrt(abs(-(\R^2*pow(cot(\th),2))+4*pow(\r,2)/pow(sin(2*\th),2)))/\R; 
ucritB(\R,\r,\th)=540-ucritA(\R,\r,\th);
umaxA(\R,\r,\th)=asin(sqrt(abs(-pow(cot(\th),2)+4*pow(\r,2)/(pow((sin(2*\th)*\R),2)))));
umaxB(\R,\r,\th)=180-umaxA(\R,\r,\th);}}
\tikzset{3d torus/.style n
args={2}{/utils/exec=\pgfmathsetmacro{\DDA}{int(sign(sin(thetacritA(#1,#2))-sin(\tdplotmaintheta)))}
  \pgfmathsetmacro{\DDB}{int(sign(sin(thetacritB(#1,#2))-sin(\tdplotmaintheta)))},
  insert path={
  plot[variable=\x,domain=1:359,smooth cycle,samples=71]
  ({torusx(\x,vcrit1(\x,\tdplotmaintheta),#1,#2)},
 {torusy(\x,vcrit1(\x,\tdplotmaintheta),#1,#2)},
 {torusz(\x,vcrit1(\x,\tdplotmaintheta),#1,#2)}) 
   \ifnum\DDA=1
    plot[variable=\x,domain=0:360,smooth cycle,samples=71]
    ({torusx(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)},
    {torusy(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)},
    {torusz(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)})    
   \else
   \ifnum\DDB=1 
    plot[variable=\x,domain={umaxA(#1,#2,\tdplotmaintheta)}:{umaxB(#1,#2,\tdplotmaintheta)},smooth,samples=71]
    ({torusx(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)},
    {torusy(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)},
    {torusz(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)})    --
    plot[variable=\x,domain={180+umaxA(#1,#2,\tdplotmaintheta)}:{180+umaxB(#1,#2,\tdplotmaintheta)},smooth,samples=71]
    ({torusx(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)},
    {torusy(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)},
    {torusz(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)})  -- cycle  
    \fi 
   \fi
  }},3d torus stretch/.style n args={2}{/utils/exec=\pgfmathsetmacro{\DDA}{int(sign(thetacritA(#1,#2)-\tdplotmaintheta))},
  insert path={\ifnum\DDA=-1
   plot[variable=\x,domain={ucritA(#1,#2,\tdplotmaintheta)}:{ucritB(#1,#2,\tdplotmaintheta)},smooth,samples=71]
    ({torusx(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)},
    {torusy(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)},
    {torusz(\x,vcrit2(\x,\tdplotmaintheta),#1,#2)}) 
  \fi 
}}}
\begin{document} 
\tdplotsetmaincoords{65}{0}
\begin{tikzpicture}[tdplot_main_coords]
     \pgfmathsetmacro{\RadiusA}{3}
     \pgfmathsetmacro{\RadiusB}{1}
     \pgfmathsetmacro{\rprime}{1.25}
     \foreach \X/\Y in {105/195,245/335}
     {\draw[line width=2mm,blue] plot[variable=\x,domain=\X:\Y,smooth]
    ({torusx(\x,2*\x,\RadiusA,\rprime)},{torusy(\x,2*\x,\RadiusA,\rprime)},{torusz(\x,2*\x,\RadiusA,\rprime)});}
     \draw[thick,samples=71,fill=gray,fill opacity=0.7,even odd
    rule,3d torus={\RadiusA}{\RadiusB}] ;
    \draw[thick,samples=71,3d torus stretch={\RadiusA}{\RadiusB}];
     \foreach \X/\Y in {-27/107,193/247}
     {\draw[line width=2mm,blue] plot[variable=\x,domain=\X:\Y,smooth]
    ({torusx(\x,2*\x,\RadiusA,\rprime)},{torusy(\x,2*\x,\RadiusA,\rprime)},{torusz(\x,2*\x,\RadiusA,\rprime)});}
  \end{tikzpicture}
\end{document}

Thank you for your time! I am not really looking for a curved or shaded line representing the trefoil though - I'd like the graph to look something like https://tex.stackexchange.com/a/148535/180771 or rather https://tex.stackexchange.com/a/70370/180771 . But how do I get the x's and o's in the certain grids, and also the straight red lines? I'd like the 'grid structure' to be preserved. I haven't constructed 3D in LaTeX before so don't really know where to begin! — JpW, Apr 26 '19 at 08:59
@JpW Well, what have you tried? Believe it or not, I believe to know what a torus is. Probably other people as well, otherwise they would not have closed your question as a duplicate of https://tex.stackexchange.com/questions/485485/square-tiling-a-torus. The functions torusx, torusy and torusz provide you with what you need in principle: they map a point with coordinates (\u,\v) to the torus. I guess one of the reasons why your question got closed is that it is hard to see effort from your side (I did not vote to close). — , Apr 26 '19 at 13:59
I did not doubt your knowledge of a torus. I just wanted to know how to put the markings on the torus since I'm a total beginner at making 3D plots. Thank you for all your help though. I also believe putting that in paper and scissors showed at least some sort of effort in trying to clarify the question. — JpW, Apr 26 '19 at 14:57

How to draw toroidal grid diagrams in TikZ

1 Answers1