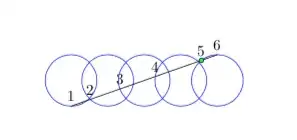
The following code renders five circles, each circle intersecting one or two other circles, and a line segment PQ. Line segment PQ intersects each circle twice. How do I label the intersection of the line segment and circle_1 at (0,-r) to be PQ_1 and the other intersection with circle_1 to be PQ_2? How do I label the intersection of the line segment and circle_2 that is "close to PQ_2" to be PQ_3, and the intersection of the line segment and circle_3 that is "close to PQ_3" to be PQ_4?
\documentclass{amsart}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage[dvipsnames]{xcolor}
\usepackage{tikz}
\usetikzlibrary{calc,intersections}
\begin{document}
\begin{tikzpicture}[x=0.25cm, y=0.25cm]
\draw[blue, name path=circle_1] let \n1={sqrt(18/pi)} in (0,0) circle (\n1);
\draw[blue, name path=circle_2] let \n1={sqrt(18/pi)} in (3.40851,0) circle (\n1);
\draw[blue, name path=circle_3] let \n1={sqrt(18/pi)} in ({2*3.40851},0) circle (\n1);
\draw[blue, name path=circle_4] let \n1={sqrt(18/pi)} in ({3*3.40851},0) circle (\n1);
\draw[blue, name path=circle_5] let \n1={sqrt(18/pi)} in ({4*3.40851},0) circle (\n1);
\path let \n1={sqrt(18/pi)} in coordinate (P) at (0,-\n1);
\path let \n1={sqrt(18/pi)}, \n2={sqrt(18/pi)} in coordinate (Q) at ({4*3.40851},\n2);
\draw[name path=PQ] (P) -- (Q);
\coordinate[name intersections={of=PQ and circle_1, by=PQ_1}];
\coordinate[name intersections={of=PQ and circle_2, by=PQ_2}];
\coordinate[name intersections={of=PQ and circle_3, by=PQ_3}];
\coordinate[name intersections={of=PQ and circle_2, by=PQ_4}];
\coordinate[name intersections={of=PQ and circle_4, by=PQ_5}];
\coordinate[name intersections={of=PQ and circle_3, by=PQ_6}];
\coordinate[name intersections={of=PQ and circle_5, by=PQ_5}];
\coordinate[name intersections={of=PQ and circle_4, by=PQ_6}];
\draw[fill=green] (PQ_5) circle (1.5pt);
\end{tikzpicture}
\end{document}


PQ_1toPQ_2going clockwise, a yellow arc fromPQ_1toPQ_2going counterclockwise, a blue arc fromPQ_3toPQ_5going clockwise, and a yellow arc fromPQ_3toPQ_5going counterclockwise? – A gal named Desire May 09 '19 at 20:47PQare to be drawn blue, and the arcs of the circles belowPQare to be drawn yellow. – A gal named Desire May 09 '19 at 21:02