I am trying to draw a histogram next to a density function, both with data from a file. The histogram is already working:
\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{pgfplots}
\begin{filecontents}{example.dat}
71
54
55
54
98
76
93
95
86
88
68
68
50
61
79
79
73
57
56
57
97
80
91
94
85
88
45
58
78
81
74
60
57
58
95
81
\end{filecontents}
\begin{document}
\begin{tikzpicture}
\begin{axis}[ybar, ymin=0]
\addplot[fill=black,
hist={
density, % <-- EDIT
bins=11
}] table [y index=0] {example.dat};
\end{axis}
\end{tikzpicture}
\end{document}
My question is with the density function. I would like to draw it using this formula (kernel density estimation):
EDIT start
where:
n: Number of datapointssigma: Standard deviation. The value of it is chosen (by me), so that the resulting curve has a specific number of local maxima. This is not part of the question and you can just use some fixed number for it, so that it looks smooth.x_i: Datapointix: Function input variable (f(x))
EDIT end
I can't just plot it using \addplot... because f(x) depends on all datapoints x_i.
I was thinking about using something like that somewhere:
\pgfplotstableread{example.dat}\table
\pgfplotstablegetrowsof{\table}
\pgfmathsetmacro{\R}{\pgfplotsretval-1}
\pgfplotsinvokeforeach{0,...,\R}{
\pgfplotstablegetelem{#1}{0}\of{\table}
\pgfmathsetmacro \value {\pgfplotsretval}
% sum up all e^0.5(\value-x)/sigma somhow
}
But I couldn't find a way to define a variable where I can add values in every iteration.
Here is an image from Wikipedia on Kernel density estimation:

The blue curve on the right is kind of what I would like to draw. What's the best way of achieving that?

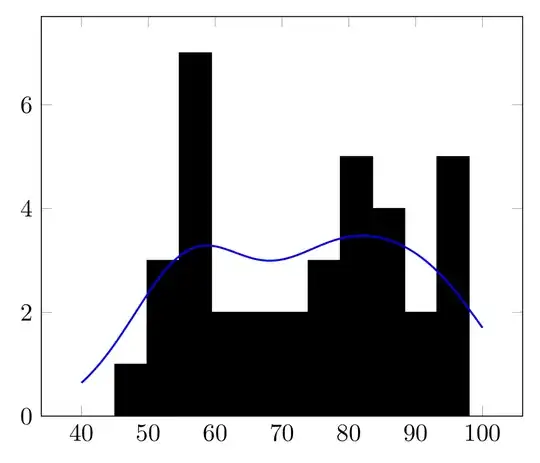





\pgfmathsetmacro{\sigma}{8}and changed your code a bit:\edef\mysum{\mysum+2*exp(-(x-\pgfplotsretval-0.5)^2)}->\edef\mysum{\mysum+1/(sqrt(2*pi)*\sigma*\R)*exp(-1/(2*\sigma*\sigma)*(x-\pgfplotsretval)^2)}. By addingdensitytohist={...}both the histogram and the KDE-function fit on one scale and the KDE-function is an actual density function (Integral == 1). My original histogram (w.o.density) is probably the reason you omitted the1/(sqrt(2*pi)*\sigma*\R)part, right? I hope my scaling is correct now... – Nathanael May 17 '19 at 00:19