Drawing text in between arrows using TIKZ

Question

Hi dear TeX community!

I hope you can help me out a bit with some matrices I have drawn (with the community's help of course) using the TIKZ package.

I think that I need to post almost the whole code so that you get an appropriate picture of the problem, so sorry for that.

\documentclass[12pt]{article} 

\usepackage{tikz}
\usetikzlibrary{positioning,matrix}

\newcommand{\mb}[1]{{\bullet #1}} % mean with bullet; dbl brackets to maintain subscript
\newcommand{\xq}{\bar{x}}
\begin{document}

    \begin{tikzpicture}

\matrix [matrix of math nodes,left delimiter=(, right delimiter=)] (mat1) {
  x_{11} & x_{22} & \ldots & x_{1j} & \ldots & x_{1k} \\ 

  x_{22} & x_{22} & \ldots & x_{2j} & \ldots & x_{2k} \\ 

  \vdots & \vdots &        & \vdots &        & \vdots \\ 

  x_{i1} & x_{i2} & \ldots & x_{ij} & \ldots & x_{ik} \\ 

  \vdots & \vdots &        & \vdots &        & \vdots \\

  x_{n1} & x_{n2} & \ldots & x_{nj} & \ldots & x_{nk} \\

};

\matrix[matrix of math nodes, left delimiter=(, right delimiter= ), below=7em of 

mat1, xshift=-8em] (mat2) {

  \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\

  \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\

  \vdots     & \vdots     &        & \vdots     &        & \vdots     \\

  \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\

  \vdots     & \vdots     &        & \vdots     &        & \vdots     \\

  \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
};

\node[anchor=west] at (mat2.south east){$\overline{x}_{\bullet \bullet} $};


\matrix[matrix of math nodes, right=4em of mat2, left delimiter=(, right delimiter=)] (mat3) {
  r_{11} & r_{12} & \ldots & r_{1j} & \ldots & r_{1k} \\

  r_{21} & r_{22} & \ldots & r_{2j} & \ldots & r_{2k} \\

  \vdots & \vdots &        & \vdots &        & \vdots \\

  r_{i1} & r_{i2} & \ldots & r_{ij} & \ldots & r_{ik} \\

  \vdots & \vdots &        & \vdots &        & \vdots \\

  r_{n1} & r_{n2} & \ldots & r_{nj} & \ldots & r_{nk} \\

};

\foreach \X/\Y in {2/{\mathrm{IN}},3/{\mathrm{ZW}}}

{\draw[-latex] (mat1) -- (mat\X);

 \draw[-latex] (mat\X.south) -- ++ (0,-4em) node[below] (G\X) 

               {$\widehat{\sigma}^2_{\Y}$};}

 \path (mat2) -- (mat3) node[midway]{$+$} (G2) -- (G3) node[midway,below=3.5em] 
(F) 

{$ \displaystyle 

F = \frac{\hat{\sigma}^2_{\mathrm{ZW}}}

         {\hat{\sigma}^2_{\mathrm{IN}}}

  = \frac{\frac{1}{k-1} \sum_{j=1}^{k} \sum_{i=1}^{n} (\xq_\mb{j} - \xq_{\bullet

\bullet})^2}


         {\frac{1}{N-k} \sum_{j=1}^{k} \sum_{i=1}^{n} (  x_{ij}   - \xq_{\bullet 
j}      )^2} 

$};

\foreach \X/\Y in {2,3}

{\draw[-latex] (G\X) -- (F);}

\end{tikzpicture}

\end{document}

So the questions that I have are

1.) Is it possible to insert this equation centered in between the uppermost two arrows?

and

2.) to draw a red "double-arrow" going from $\bar{x}_{\bullet 1}$ to $\bar{x}_{\bullet \bullet}$ and one from $r_{11}$ to \bar{x}_{\bullet 1}?

Thank you guys so so much!

This is what it looks like at the moment:

This is the output I kind of imagined (roughly):

Welcome to TeX.SE! For the first request, which formula are you referring to? Also how should the red line be placed? I hope if you could you paint or another program to show us the desired output (make it rough, it doesn't need to be fancy, but meaningful) :) — M. Al Jumaily, Jun 15 '19 at 19:45
If you like an answer and it was helpful, please consider upvoting (by clicking on the arrows next to the score) and marking it as accepted answer (by clicking on the checkmark ✓). @Ñako surely deserves a tick after all of the work that they have put in! — , Jun 26 '19 at 00:44

Ñako · Answer 1 · 2019-06-19T20:53:42.650

Further attempts with full information

My fourth attempt:

Customizing arrows style.

There are many ways to costumize the arrow style with tikz, see the documentation, Chapter 16 (p.186). In this case, by editing the double arrow/.style in the preamble and/or the options of the last two draw commands of the code you can display "more elegant" arrows:

custom-based double-headed arrow:

Code:

% From https://tex.stackexchange.com/a/72793/89320, customize for double-headed arrows
\tikzset{
double arrow/.style args={#1 colored by #2 and #3}{
    stealth-stealth,line width=#1,#2, % first arrow
    postaction={draw,stealth-stealth,#3,line width=(#1)/3,
        shorten <=2*(#1)/3,shorten >=2*(#1)/3}, % second arrow
  }
}

  \draw[double arrow=2pt colored by red and white!80!, opacity=0.75,] (mat2-1-1.north) to [in=80,out=30]  (xpp.north);
  \draw[double arrow=2pt colored by red and white!80!, opacity=0.75,] ([yshift=2pt]mat3-1-1.north) to [in=20,out=160] (mat2-1-1.north);

double and <->:

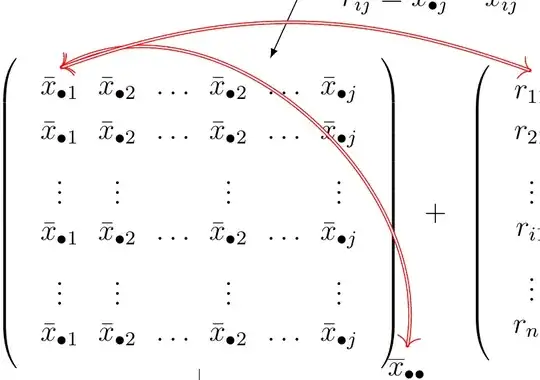
Code:

\draw[red, double,<->] (mat2-1-1.north) to [in=80,out=30]  (xpp.north);
\draw[red, double,<->] ([yshift=2pt]mat3-1-1.north) to [in=20,out=160] (mat2-1-1.north);

double and Latex-Latex:

Code:

\draw[red, {Latex[length=2mm, width=2mm]}-{Latex[length=2mm, width=2mm]} ,double, double distance=.5pt] (mat2-1-1.north) to [in=80,out=30]  (xpp.north);
\draw[red, {Latex[length=2mm, width=2mm]}-{Latex[length=2mm, width=2mm]} ,double, double distance=.5pt] ([yshift=2pt]mat3-1-1.north) to [in=20,out=160] (mat2-1-1.north);

My third attempt:

The desired output is yet known:

No need of tikznode, cell matrix referencing solution given by Andrew and also in the comments by CarLaTeX
double arrow/.style taken from Arrow with two colors with TikZ

Here is my approach:

Code:

\documentclass[12pt]{article} 

\usepackage{tikz}
\usetikzlibrary{positioning,matrix}
\usetikzlibrary{arrows, arrows.meta, calc,fadings}

\newcommand{\mb}[1]{{\bullet #1}} % mean with bullet; dbl brackets to maintain subscript
\newcommand{\xq}{\bar{x}}

% From https://tex.stackexchange.com/a/72793/89320
\tikzset{
    double arrow/.style args={#1 colored by #2 and #3}{
        -stealth,line width=#1,#2, % first arrow
        postaction={draw,-stealth,#3,line width=(#1)/3,
            shorten <=(#1)/3,shorten >=2*(#1)/3}, % second arrow
    }
}
%---------------------------------------------------

\begin{document}

    \begin{tikzpicture}

    \matrix [anchor=center,matrix of math nodes,left delimiter=(, right delimiter=)] (mat1) {
      x_{11} & x_{22} & \ldots & x_{1j} & \ldots & x_{1k} \\ 
      x_{22} & x_{22} & \ldots & x_{2j} & \ldots & x_{2k} \\ 
      \vdots & \vdots &        & \vdots &        & \vdots \\ 
      x_{i1} & x_{i2} & \ldots & x_{ij} & \ldots & x_{ik} \\ 
      \vdots & \vdots &        & \vdots &        & \vdots \\
      x_{n1} & x_{n2} & \ldots & x_{nj} & \ldots & x_{nk} \\
    };


    \matrix[anchor=center,matrix of math nodes, left delimiter=(, right delimiter= ), below=7em of mat1, xshift=-8em] (mat2) {
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
      \vdots     & \vdots     &        & \vdots     &        & \vdots     \\
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
      \vdots     & \vdots     &        & \vdots     &        & \vdots     \\
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
    };

    \node[anchor=west] (xpp) at (mat2.south east){$\overline{x}_{\bullet \bullet} $};


    \matrix[anchor=center,matrix of math nodes, right=4em of mat2, left delimiter=(, right delimiter=)] (mat3) {
      r_{11} & r_{12} & \ldots & r_{1j} & \ldots & r_{1k} \\
      r_{21} & r_{22} & \ldots & r_{2j} & \ldots & r_{2k} \\
      \vdots & \vdots &        & \vdots &        & \vdots \\
      r_{i1} & r_{i2} & \ldots & r_{ij} & \ldots & r_{ik} \\
      \vdots & \vdots &        & \vdots &        & \vdots \\
      r_{n1} & r_{n2} & \ldots & r_{nj} & \ldots & r_{nk} \\
    };

    \coordinate (aux) at ($ (mat1) !.5! (mat2) $);
    \node[anchor=center,](xij) at (mat1 |- aux) {$ \displaystyle 
        x_{ij}=\xq_\mb{j}+r_{ij}$};
    \node[anchor=center, below =-2pt of xij] (rij) {$ \displaystyle
        r_{ij}=\xq_\mb{j}-x_{ij}$};
    %
    \foreach \X/\Y in {2/{\mathrm{IN}},3/{\mathrm{ZW}}}
    {\draw[-latex] (mat1) -- (mat\X); 
    \draw[-latex] (mat\X.south) -- ++ (0,-4em) node[below] (G\X) {$\widehat{\sigma}^2_{\Y}$};}
    \path (mat2) -- (mat3) node[midway]{$+$} (G2) -- (G3) node[midway,below=3.5em] (F) 
    {$ \displaystyle 
        F = \frac{\hat{\sigma}^2_{\mathrm{ZW}}}
        {\hat{\sigma}^2_{\mathrm{IN}}}
        = \frac{\frac{1}{k-1} \sum_{j=1}^{k} \sum_{i=1}^{n} (\xq_\mb{j} - \xq_{\bullet\bullet})^2}
        {\frac{1}{N-k} \sum_{j=1}^{k} \sum_{i=1}^{n} (x_{ij}-\xq_{\bullet j})^2}
    $};
    \foreach \X/\Y in {2,3} {\draw[-latex] (G\X) -- (F);}

    \draw[double arrow=10pt colored by blue!50!white and red!50!white,opacity=0.75] (mat2-1-1.north) to[in=80,out=30]  (xpp.north);
    \draw[double arrow=10pt colored by blue!50!white and red!50!white,opacity=0.75] ([yshift=2pt]mat3-1-1.north) to[in=20,out=160] (mat2-1-1.north);

    \end{tikzpicture}

\end{document}

First attempts with partial information

I have tried to figure out what it could be your desired output. For this purpose:

I have defined the command \tikznode[..options..]{..label..}{..contents..} in the preamble, which is the solution by gernot to How to add arrow in equations and matrix?,to mark the contents you want to join with arrows. The main reason is that the tikzmark library did not work in my case:
```
\newcommand\tikznode[3][]%
{\tikz[remember picture,baseline=(#2.base)]
\node[minimum size=0pt,inner sep=0pt,#1](#2){#3};%
 }
```
I have also added following the arrows, arrows.meta, calc tikzlibraries.

To your questions:

I have placed the equation F between the matrices and commented %\displaystyle so that it passes between the uppermost two arrows:

\coordinate (aux) at ($ (mat1) !.5! (mat2) $);
\node[anchor=center,](F) at (mat1 |- aux) {$ %\displaystyle 
    F = \frac{\hat{\sigma}^2_{\mathrm{ZW}}}
    {\hat{\sigma}^2_{\mathrm{IN}}}
    = \frac{\frac{1}{k-1} \sum_{j=1}^{k} \sum_{i=1}^{n} (\xq_\mb{j} - \tikznode{xpp2}{$\xq_{\bullet\bullet}$})^2}
    {\frac{1}{N-k} \sum_{j=1}^{k} \sum_{i=1}^{n} (x_{ij}-\xq_{\bullet j})^2}
    $};

There are two $\xq_{\bullet \bullet}$ (I mean $\bar{x}_{\bullet \bullet}$ ). Which one do you mean? The matrix (red arrow) or the equation (orange arrow) one?

Could you please specify or better include an image of your desired output?

My second attempt:

1st improvements:

Direct referencing the matrix cells with matname-rownumber-columnnumber instead of \tikznode, which is the approach/solution of Andrew (with your permission of course)
Added round corners and the arrows go around the matrices for better readability

Output:

Code:

\documentclass[12pt]{article} 

\usepackage{tikz}
\usetikzlibrary{positioning,matrix}
\usetikzlibrary{arrows, arrows.meta, calc, tikzmark}

\newcommand{\mb}[1]{{\bullet #1}} % mean with bullet; dbl brackets to maintain subscript
\newcommand{\xq}{\bar{x}}

    %Tikznode -> https://tex.stackexchange.com/a/361392/89320
\newcommand\tikznode[3][]%
{\tikz[remember picture,baseline=(#2.base)]
    \node[minimum size=0pt,inner sep=0pt,#1](#2){#3};%
}
%-----

\begin{document}

    \begin{tikzpicture}[remember picture]

    \matrix [anchor=center,matrix of math nodes,left delimiter=(, right delimiter=)] (mat1) {
      x_{11} & x_{22} & \ldots & x_{1j} & \ldots & x_{1k} \\ 
      x_{22} & x_{22} & \ldots & x_{2j} & \ldots & x_{2k} \\ 
      \vdots & \vdots &        & \vdots &        & \vdots \\ 
      x_{i1} & x_{i2} & \ldots & x_{ij} & \ldots & x_{ik} \\ 
      \vdots & \vdots &        & \vdots &        & \vdots \\
      x_{n1} & x_{n2} & \ldots & x_{nj} & \ldots & x_{nk} \\
    };


    \matrix[anchor=center,matrix of math nodes, left delimiter=(, right delimiter= ), below=7em of mat1, xshift=-8em] (mat2) {
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
      \vdots     & \vdots     &        & \vdots     &        & \vdots     \\
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
      \vdots     & \vdots     &        & \vdots     &        & \vdots     \\
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
    };

    \node[anchor=west] (xpp) at (mat2.south east){$\overline{x}_{\bullet \bullet} $};


    \matrix[anchor=center,matrix of math nodes, right=4em of mat2, left delimiter=(, right delimiter=)] (mat3) {
      r_{11} & r_{12} & \ldots & r_{1j} & \ldots & r_{1k} \\
      r_{21} & r_{22} & \ldots & r_{2j} & \ldots & r_{2k} \\
      \vdots & \vdots &        & \vdots &        & \vdots \\
      r_{i1} & r_{i2} & \ldots & r_{ij} & \ldots & r_{ik} \\
      \vdots & \vdots &        & \vdots &        & \vdots \\
      r_{n1} & r_{n2} & \ldots & r_{nj} & \ldots & r_{nk} \\
    };

    \coordinate (aux) at ($ (mat1) !.5! (mat2) $);
    \node[anchor=center,](F) at (mat1 |- aux) {$ %\displaystyle 
        F = \frac{\hat{\sigma}^2_{\mathrm{ZW}}}
        {\hat{\sigma}^2_{\mathrm{IN}}}
        = \frac{\frac{1}{k-1} \sum_{j=1}^{k} \sum_{i=1}^{n} (\xq_\mb{j} - \tikznode{xpp2}{$\xq_{\bullet\bullet}$})^2}
        {\frac{1}{N-k} \sum_{j=1}^{k} \sum_{i=1}^{n} (x_{ij}-\xq_{\bullet j})^2}
        $};
     %                      
    \foreach \X/\Y in {2/{\mathrm{IN}},3/{\mathrm{ZW}}}
    {\draw[-latex] (mat1.south) -- ++(0,-1.5em) -|  ([yshift=0.1em]mat\X.north);
     \draw[-latex] (mat\X.south) -- ++ (0,-4em) node[below] (G\X) {$\widehat{\sigma}^2_{\Y}$};}
     \path (mat2) -- (mat3) node[midway]{$+$} (G2) -- (G3) node[midway,below=3.5em] {}; %(F)

    \draw[latex'-latex',red,rounded corners=2mm] (mat2-1-1.north) -- +(0,0.4) -|(xpp.north);
    \draw[latex'-latex',red,rounded corners=2mm] (mat2-1-1.north) -- +(0,0.4) -|(mat3-1-1.north);
    \draw[latex'-latex',orange,rounded corners=2mm] (mat2-1-1.north)-- +(0,2.25) -| (xpp2.north);
    \end{tikzpicture}

\end{document}

My first attempt:

Output: Code:

\documentclass[12pt]{article} 

\usepackage{tikz}
\usetikzlibrary{positioning,matrix}
\usetikzlibrary{arrows, arrows.meta, calc}

\newcommand{\mb}[1]{{\bullet #1}} % mean with bullet; dbl brackets to maintain subscript
\newcommand{\xq}{\bar{x}}

%Tikznode -> https://tex.stackexchange.com/a/361392/89320
\newcommand\tikznode[3][]%
{\tikz[remember picture,baseline=(#2.base)]
    \node[minimum size=0pt,inner sep=0pt,#1](#2){#3};%
}
%-----

\begin{document}

    \begin{tikzpicture}

    \matrix [anchor=center,matrix of math nodes,left delimiter=(, right delimiter=)] (mat1) {
      x_{11} & x_{22} & \ldots & x_{1j} & \ldots & x_{1k} \\ 
      x_{22} & x_{22} & \ldots & x_{2j} & \ldots & x_{2k} \\ 
      \vdots & \vdots &        & \vdots &        & \vdots \\ 
      x_{i1} & x_{i2} & \ldots & x_{ij} & \ldots & x_{ik} \\ 
      \vdots & \vdots &        & \vdots &        & \vdots \\
      x_{n1} & x_{n2} & \ldots & x_{nj} & \ldots & x_{nk} \\
    };


    \matrix[anchor=center,matrix of math nodes, left delimiter=(, right delimiter= ), below=7em of mat1, xshift=-8em] (mat2) {
      \tikznode{xp1}{$\xq_\mb{1}$} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
      \vdots     & \vdots     &        & \vdots     &        & \vdots     \\
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
      \vdots     & \vdots     &        & \vdots     &        & \vdots     \\
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
    };

    \node[anchor=west] at (mat2.south east){\tikznode{xpp}{$\overline{x}_{\bullet \bullet} $}};


    \matrix[anchor=center,matrix of math nodes, right=4em of mat2, left delimiter=(, right delimiter=)] (mat3) {
      \tikznode{r11}{$r_{11}$} & r_{12} & \ldots & r_{1j} & \ldots & r_{1k} \\
      r_{21} & r_{22} & \ldots & r_{2j} & \ldots & r_{2k} \\
      \vdots & \vdots &        & \vdots &        & \vdots \\
      r_{i1} & r_{i2} & \ldots & r_{ij} & \ldots & r_{ik} \\
      \vdots & \vdots &        & \vdots &        & \vdots \\
      r_{n1} & r_{n2} & \ldots & r_{nj} & \ldots & r_{nk} \\
    };

    \coordinate (aux) at ($ (mat1) !.5! (mat2) $);
    \node[anchor=center,](F) at (mat1 |- aux) {$ %\displaystyle 
    F = \frac{\hat{\sigma}^2_{\mathrm{ZW}}}
    {\hat{\sigma}^2_{\mathrm{IN}}}
    = \frac{\frac{1}{k-1} \sum_{j=1}^{k} \sum_{i=1}^{n} (\xq_\mb{j} - \tikznode{xpp2}{$\xq_{\bullet\bullet})^2$}}
    {\frac{1}{N-k} \sum_{j=1}^{k} \sum_{i=1}^{n} (x_{ij}-\xq_{\bullet j})^2}
    $};


    \foreach \X/\Y in {2/{\mathrm{IN}},3/{\mathrm{ZW}}}
    {\draw[-latex] (mat1.south) -- ++(0,-1.5em) -|  ([yshift=0.4em]mat\X.north);
     \draw[-latex] (mat\X.south) -- ++ (0,-4em) node[below] (G\X) {$\widehat{\sigma}^2_{\Y}$};}
     \path (mat2) -- (mat3) node[midway]{$+$} (G2) -- (G3) node[midway,below=3.5em] {}; %(F)

    \end{tikzpicture}
    \begin{tikzpicture}[remember picture,overlay]
    \draw[latex'-latex',red] (xp1)--(xpp);
    \draw[latex'-latex',red] (xp1.north) |- +(0,0.4) -|(r11.north);
    \draw[latex'-latex',orange] (xp1)--(xpp2);
    \end{tikzpicture}

\end{document}

There is no need to use a \tikznode in a TikZ matrix (and in some cases could lead to errors), you can simply reference the cell with matname-rownumber-columnnumber, for example mat1-1-1, or adding |[name=nodename]| before the cell content, for example |[name=r11]|r_11. — CarLaTeX, Jun 16 '19 at 04:51
@CarLaTeX, I was editing my answer and after posting it I saw Andre´s one with this easy referencing. One learn always new things :) — Ñako, Jun 16 '19 at 08:01
@CarLaTeX, what about referencing the equation´s term $\bar{x}_{\bullet \bullet}$ with the matrix´s term? With tikzmark I get Package tikz Error: Cannot parse this coordinate. ...\sum_{i=1}^{n} (x_{ij}-\xq_{\bullet j})^2}, but it works with tikznode. Then using tikznode and the matrix cell referencing, i.e., adding \draw[latex'-latex',orange] (mat2-1-1)--(xpp2); to the same tikzpicture or just to a new tikzpicture with [remember picture,overlay] it does not give the desired output — Ñako, Jun 16 '19 at 08:49
To name an ordinary node you should do: \node[anchor=west] (xpp) at (mat2.south east){$\overline{x}_{\bullet \bullet}$}; or \node[anchor=west, name=xpp] at (mat2.south east){$\overline{x}_{\bullet \bullet}$}; (hoping to have underdstood what you asked). — CarLaTeX, Jun 16 '19 at 09:39
@CarLaTeX, not really. I mean the orange arrow between the $\bar{x}_{\bullet \bullet}$ (that is $\xq_{\bullet \bullet}$ ) of the F equation and the $\bar{x}_{\bullet 1}$ (that is $\xq_{\bullet 1}$ ) of matrix 1. Which is the best way to reference a equation´s term in this case? — Ñako, Jun 16 '19 at 09:54
Hi guys! Thank you people so so much for your input. You have helped me out already so much and your suggestions actually look much nicer than what I had imagined.
I have edited my question now with a rough idea of the output but as I have said your suggestions actually look way nicer plus you have also included the double arrow, which is pretty important to me.

Also, I have now included the desired equation in between the arrows (Sorry I forgot to be explicit about which equation should be included).

Thank you guys one more time so much. :) — NoName, Jun 16 '19 at 16:12
You can't reference because you have to put [remember picture] also in the first picture, see here: https://www.overleaf.com/read/qgfqrjmptkhm. To tell the true, in this case, you can use only one tikzpicture environment, without [remember picture] at all. — CarLaTeX, Jun 16 '19 at 19:08
@CarLaTeX, thanks for the explanation. I have found by myself these two key points. In my second approach I have added remember picture and in the third one I have deleted it. Thanks anyway — Ñako, Jun 16 '19 at 19:52
@Ñako Sorry for not having replied early but I had no time before. Btw, +1! — CarLaTeX, Jun 16 '19 at 19:55
@Nako Thank you so much for your hard work and so many attempts.
Do you know how I can specify the arrows to make them look smaller and more elegant just as they were in your second attempt but with everything else staying the same? So just instead of using this big, bright arrows I would like to use small, red double arrows? Also, the equation that you have inserted in your third attempt in between the two arrows should stay in place.

Thank you and 1+ definitely — NoName, Jun 19 '19 at 07:12
@Ñako Thank you! That is so logical somehow if you explain it. My professor told me to draw the double arrow using <-->. However, if I try that I get the warning: Package pgf Error: Unknown arrow tip kind '->'. \draw[red, double,<-->].
So obviously, he was not right about that code. Do you have any idea? So I basically just want the tip to show in both directions ( like <--> ) if you know what I mean lol. — NoName, Jun 19 '19 at 19:16
@NoName. Sorry, It was a little confusing to me, what does double arrow mean to you; an arrow with two lines (see your desired output) or an arrow with two heads? At the end both. You have a typo, you can draw the double headed arrow using <-> (only one minus), but not with <--> (two minus). I have edited the last (fourth) attempt. — Ñako, Jun 19 '19 at 20:54

score 2 · Answer 2 · answered Jun 16 '19 at 00:42

I am not sure what you mean by "inserting the equation" in (1) but the arrows you can draw using the node coordinates of the matrices. For example, the \bar{x}_{\bullet 1} entry is the node (mat2-1-1) and the r_{11} entry is (mat3-1-1). Below I have named the \bar{x}_{\bullet \bullet} entry BB so you can draw a double red line from r_{11} to \bar{x}_{\bullet \bullet} using

  \draw[red, double,->](mat2-1-1)--(BB);

I am not sure if this is really what you want however as the arrow will go through the other matrix entries. Instead, if you use

\draw[red, double,->](mat3-1-1) to[out=150,in=30] (mat2-1-1);

the the arrow will go around the matrices. The code below gives red and blue arrows to give you different options:

If you can explain in more detail what you want for (1) I will try and answer that too. Here is the code:

\documentclass[12pt]{article}

\usepackage{tikz}
\usetikzlibrary{positioning,matrix}

\newcommand{\mb}[1]{{\bullet #1}} % mean with bullet; dbl brackets to maintain subscript
\newcommand{\xq}{\bar{x}}
\begin{document}

  \begin{tikzpicture}

    \matrix[matrix of math nodes,left delimiter=(, right delimiter=)] (mat1) {
      x_{11} & x_{22} & \ldots & x_{1j} & \ldots & x_{1k} \\
      x_{22} & x_{22} & \ldots & x_{2j} & \ldots & x_{2k} \\
      \vdots & \vdots &        & \vdots &        & \vdots \\
      x_{i1} & x_{i2} & \ldots & x_{ij} & \ldots & x_{ik} \\
      \vdots & \vdots &        & \vdots &        & \vdots \\
      x_{n1} & x_{n2} & \ldots & x_{nj} & \ldots & x_{nk} \\
    };

    \matrix[matrix of math nodes, left delimiter=(, right delimiter= ),
             below=7em of mat1, xshift=-8em] (mat2) {
      \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
    \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
    \vdots     & \vdots     &        & \vdots     &        & \vdots     \\
    \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
    \vdots     & \vdots     &        & \vdots     &        & \vdots     \\
    \xq_\mb{1} & \xq_\mb{2} & \ldots & \xq_\mb{2} & \ldots & \xq_\mb{j} \\
  };

  \node[anchor=west] (BB) at (mat2.south east){$\overline{x}_{\bullet \bullet} $};
  \matrix[matrix of math nodes, right=4em of mat2, left delimiter=(, right delimiter=)] (mat3) {
    r_{11} & r_{12} & \ldots & r_{1j} & \ldots & r_{1k} \\
      r_{21} & r_{22} & \ldots & r_{2j} & \ldots & r_{2k} \\
      \vdots & \vdots &        & \vdots &        & \vdots \\
      r_{i1} & r_{i2} & \ldots & r_{ij} & \ldots & r_{ik} \\
      \vdots & \vdots &        & \vdots &        & \vdots \\
      r_{n1} & r_{n2} & \ldots & r_{nj} & \ldots & r_{nk} \\
    };

  \foreach \X/\Y in {2/{\mathrm{IN}},3/{\mathrm{ZW}}} {
   \draw[-latex] (mat1) -- (mat\X);
   \draw[-latex] (mat\X.south) -- ++ (0,-4em) node[below] (G\X)
                 {$\widehat{\sigma}^2_{\Y}$};
                 }
   \path (mat2) -- (mat3) node[midway]{$+$} (G2) -- (G3) node[midway,below=3.5em] (F)
  {$ \displaystyle
  F = \frac{\hat{\sigma}^2_{\mathrm{ZW}}}
           {\hat{\sigma}^2_{\mathrm{IN}}}
    = \frac{\frac{1}{k-1} \sum_{j=1}^{k} \sum_{i=1}^{n} (\xq_\mb{j} - \xq_{\bullet\bullet})^2}
           {\frac{1}{N-k} \sum_{j=1}^{k} \sum_{i=1}^{n} (  x_{ij}   - \xq_{\bullet j})^2}
  $};

  \foreach \X/\Y in {2,3}
     {\draw[-latex] (G\X) -- (F);}

  \draw[red, double,->](mat2-1-1)--(BB);
  \draw[red, double,->](mat3-1-1)--(mat2-1-1);

  \draw[blue, double,->](mat2-1-1) to[out=210, in=150] (mat2-6-1.south west) to[out=330, in=190] (BB);
  \draw[blue, double,->](mat3-1-1) to[out=150,in=30] (mat2-1-1);

  \end{tikzpicture}

\end{document}

I guess "inserting the equation" means something like this ----- equation here ---> — , Jun 16 '19 at 15:37

Drawing text in between arrows using TIKZ

2 Answers2

Further attempts with full information

My fourth attempt:

My third attempt:

First attempts with partial information

My second attempt:

My first attempt: