Triangle on 3d sphere

Question

I want to draw a correct triangle on the surface of a sphere. But I don't know how to draw the curved lines correctly. Besides I did not want to start calculating with sine and cosine. One point of the triangle must be located on the north pole.

Could anybody help me! It is highly appreciated!

\documentclass[border=5mm]{standalone}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}

\draw[thick,->] (0,0,0) -- (0,3,0) node[anchor=north west]{$z$};


  \shade[ball color = gray!40, opacity = 0.4] (0,0) circle (2cm);
  \draw (0,0) circle (2cm);
  \draw (-2,0) arc (180:360:2 and 0.6);
  \draw[dashed] (2,0) arc (0:180:2 and 0.6);
  \fill[fill=black] (0,0) circle (1pt);



\end{tikzpicture}
\end{document}

Maybe make yourself familiar with https://tex.meta.stackexchange.com/questions/228. — Dr. Manuel Kuehner, Jun 21 '19 at 11:28

score 6 · Answer 1 · edited Jun 21 '19 at 14:02

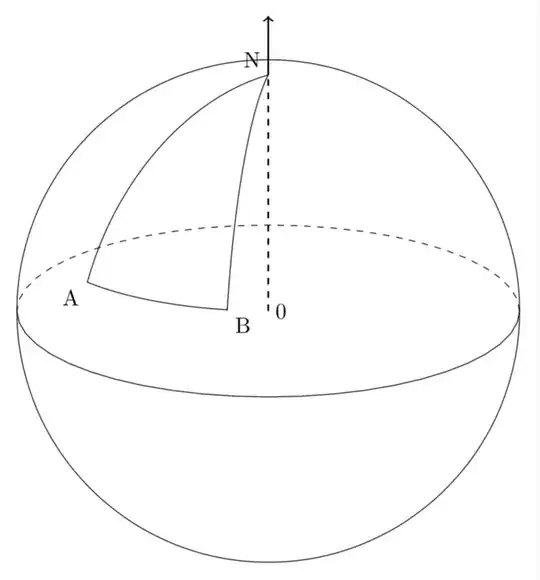
Modified from the good answer of the friendly creature named marmot https://tex.stackexchange.com/a/471670/191410

\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3d}
\begin{document}
\tdplotsetmaincoords{90}{-30}
\begin{tikzpicture}[tdplot_main_coords]
\pgfmathsetmacro{\Radius}{4}
\pgfmathsetmacro{\radius}{3.6}
\draw[tdplot_screen_coords] (0,0) circle (\Radius);
\begin{scope}
\draw plot[variable=\x,domain=-20:20] (xyz spherical cs:radius=\Radius,latitude=20,longitude=\x)
-- plot[variable=\x,domain=20:90] (xyz spherical cs:radius=\Radius,latitude=\x,longitude=20)
-- plot[variable=\x,domain=90:20] (xyz spherical cs:radius=\Radius,latitude=\x,longitude=-20);
\end{scope}
\draw[thick,->] (0,0,0) -- (0,0,5);
\draw[tdplot_screen_coords,dashed] (0,0) ellipse (4 and 0.5);

\node[anchor=north east] at (xyz spherical cs:radius=\Radius,latitude=20,longitude=-20) {A};
\node[anchor=north west] at (xyz spherical cs:radius=\Radius,latitude=20,longitude=20) {B};
\node[anchor=south east] at (xyz spherical cs:radius=\Radius,latitude=90,longitude=-20) {N};
\node[anchor=west] at (xyz spherical cs:radius=0,latitude=0,longitude=0) {0};
\end{tikzpicture}
\end{document}

Or

\documentclass[tikz,border=3.14mm]{standalone}
\usepackage{tikz-3dplot}
\begin{document}
\tdplotsetmaincoords{110}{-30}
\begin{tikzpicture}[tdplot_main_coords]
 \pgfmathsetmacro{\Radius}{4}
 \draw[tdplot_screen_coords] (0,0) circle (\Radius);
 \begin{scope}
  \draw plot[variable=\x,domain=-20:20] (xyz spherical cs:radius=\Radius,latitude=20,longitude=\x)
  -- plot[variable=\x,domain=20:90] (xyz spherical cs:radius=\Radius,latitude=\x,longitude=20)
  -- plot[variable=\x,domain=90:20] (xyz spherical cs:radius=\Radius,latitude=\x,longitude=-20);
 \end{scope}
 \draw[thick,dashed] (0,0,0) -- (0,0,\Radius);
 \draw[thick,->] (0,0,\Radius) -- (0,0,5);
 \draw[dashed] plot[variable=\x,domain=90-\tdplotmainphi:270-\tdplotmainphi] 
 (xyz spherical cs:radius=\Radius,latitude=0,longitude=\x);
 \draw plot[variable=\x,domain=90-\tdplotmainphi:-90-\tdplotmainphi] 
 (xyz spherical cs:radius=\Radius,latitude=0,longitude=\x);
 \node[anchor=north east] at (xyz spherical cs:radius=\Radius,latitude=20,longitude=-20) {A};
 \node[anchor=north west] at (xyz spherical cs:radius=\Radius,latitude=20,longitude=20) {B};
 \node[anchor=south east] at (xyz spherical cs:radius=\Radius,latitude=90,longitude=-20) {N};
 \node[anchor=west] at (xyz spherical cs:radius=0,latitude=0,longitude=0) {0};
\end{tikzpicture}
\end{document}

@KJO I give a link where there code is originally from. Is this not enough of mentioning? — gigi, Jun 21 '19 at 12:58
Thanks. From a geometrical point of view shouldn't the straight line of the triangle also be curved since we are on a sphere? — mscm, Jun 21 '19 at 13:03
@mscm The curvature of the triangles bottom line depends on the view point. For example \tdplotsetmaincoords{100}{-30} will give a slightly curved line — gigi, Jun 21 '19 at 13:11
@gigi I see, you are right. I tried this little change, but then the north pole is not fixed anymore. — mscm, Jun 21 '19 at 13:20
@mscm The north pole is no longer fixed, because you look from another direction onto the globe — gigi, Jun 21 '19 at 13:21

Triangle on 3d sphere

1 Answers1