I saw this answer How to draw this arc (intersection of a plane and a sphere) automatically? and tried to draw this sphere. But, I can't obtain the correct result. How can I get the correct result?
\documentclass[tikz,border=1mm, 12 pt]{standalone}
\usepackage{tikz-3dplot}
\usepackage{fouriernc}
\usetikzlibrary{intersections,calc,backgrounds}
\makeatletter
% retrieves the 3D coordinates
\def\RawCoord(#1){\csname tikz@dcl@coord@#1\endcsname}%
\def\scalprod#1=#2.#3;{%
\edef\coordA{\RawCoord#2}%
\edef\coordB{\RawCoord#3}%
\pgfmathsetmacro\pgfutil@tmpa{scalarproduct({\coordA},{\coordB})}
\edef#1{\pgfutil@tmpa}}%
\makeatother
\newcommand{\spaux}[6]{(#1)*(#4)+(#2)*(#5)+(#3)*(#6)}
\pgfmathdeclarefunction{scalarproduct}{2}{% scalar product of two 3-vectors
\begingroup%
\pgfmathparse{\spaux#1#2}%
\pgfmathsmuggle\pgfmathresult\endgroup}
\tikzset{reverseclip/.style={insert path={(current bounding box.south west) -- (current bounding box.north west) -- (current bounding box.north east) --(current bounding box.south east) -- cycle} }}
\begin{document}
\tdplotsetmaincoords{70}{50}
\begin{tikzpicture}[scale=1,tdplot_main_coords,declare function={R=5*sqrt(7)*(1/3);r=5*sqrt(3)*(1/3);
alpha1(\th,\ph,\b)=\ph+asin(cot(\th)*tan(\b));%
alpha2(\th,\ph,\b)=-180+\ph-asin(cot(\th)*tan(\b));%
beta1(\th,\ph,\a)=90+atan(cot(\th)/sin(\a-\ph));%
beta2(\th,\ph,\a)=270+atan(cot(\th)/sin(\a-\ph));%
}]
\path
(5/2, {5* sqrt(3)/6}, 0) coordinate (O)
(0,0, 0) coordinate (A)
(5, 0, 0) coordinate (B)
(5/2, {5* sqrt(3)/2}, 0) coordinate (C)
(32/5,0, 24/5) coordinate (S)
(5/2, 0, 10/3) coordinate (I)
(5/2, {5* sqrt(3)/6}, 10/3) coordinate (T)
($ (A)!0.5!(B) $) coordinate (M)
(0,0,1) coordinate(Z);
\begin{scope}[tdplot_screen_coords, on background layer]
\draw[thick,name path global=ball] (T) circle (R);
\end{scope}
\begin{scope}[canvas is xy plane at z={0}]
\draw[dashed,cyan] (O) circle (r);
\scalprod\myz=(T).(Z); % z component of T
\pgfmathsetmacro{\myel}{atan(-1*\myz/r)}
\draw[thick] ({alpha1(\tdplotmaintheta,\tdplotmainphi,{\myel})}:r)
arc({alpha1(\tdplotmaintheta,\tdplotmainphi,{\myel})}:
{alpha2(\tdplotmaintheta,\tdplotmainphi,{\myel})}:r) ;
\end{scope}
\begin{scope}[canvas is xz plane at y={0}]
\draw[dashed,red,name path=c1] (I) circle (25/6);
\clip[name intersections={of=c1 and ball,total=\t}]
let \p1=($(intersection-1)-(I)$),\n1={atan2(\y1,\x1)+180},\n2={2*veclen(\y1,\x1)} in
(intersection-1) -- ++ (\n1:\n2) -- (current bounding box.north west)
-- (current bounding box.south west) -- cycle;
\draw[thick] (I) circle (25/6);
\end{scope}
\begin{scope}[on background layer]
\foreach \v/\position in {T/above,O/below,A/below,B/below,C/below,S/right,I/above,M/below} {
\draw[draw =black, fill=black] (\v) circle (1.2pt) node [\position=0.2mm] {$\v$};
}
\end{scope}
\foreach \X in {A,B,C} \draw[dashed] (\X) -- (S);
\draw[dashed] (A) -- (B) -- (C) -- cycle
(T) -- (I) -- (M) -- (O) -- cycle
;
\end{tikzpicture}
\end{document}

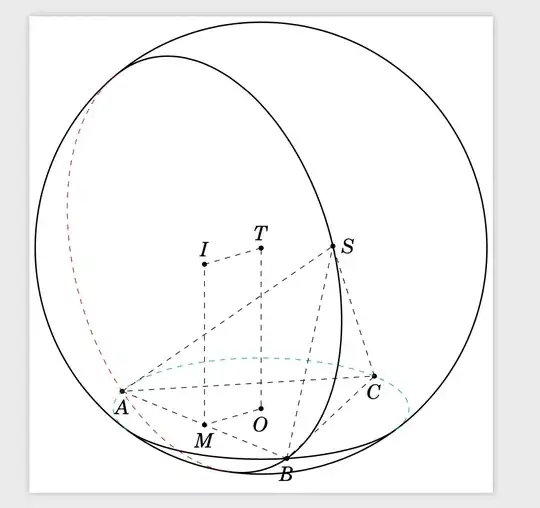
T, andO, which often denotes the origin, have nontrivialxandycomponents. Why? What is the purpose of these conventions? (The first arc works as expected if you use\draw[thick] ($(O)+({alpha1(\tdplotmaintheta,\tdplotmainphi,{\myel})}:r)$) arc({alpha1(\tdplotmaintheta,\tdplotmainphi,{\myel})}: {alpha2(\tdplotmaintheta,\tdplotmainphi,{\myel})}:r) ;, i.e. shift its center appropriately.) – Sep 04 '19 at 03:03(-5/2, {-5* sqrt(3)/6}, 0) coordinate (V)to getOat origin. E.g.($ (5/2, {5* sqrt(3)/6}, 0) + (V) $) coordinate (O)Similarly to every points. – minhthien_2016 Sep 04 '19 at 03:11Iand why the radius of the red dashed circle is 25/6, which is greater thanr=5/sqrt(3). This seems to be part of a larger sphere. If you want to draw a visible arc, it should be the visible arc on that sphere. Clearly I am missing something basic. – Sep 04 '19 at 03:26alpha1andalpha2are for latitude circles on a sphere. One needs to know which sphere one is considering. – Sep 04 '19 at 03:28Circumsphere[{{0, 0}, {5, 0}, {32/5, 24/5}}]to find center and radius of the circumcircleSABand I put the triangle in the planey=0. – Thuy Nguyen Sep 04 '19 at 03:3525/6withR=5*sqrt(7)*(1/3). – Thuy Nguyen Sep 04 '19 at 03:45