Ellipse in perspective plane around 2 points in 3d space

Question

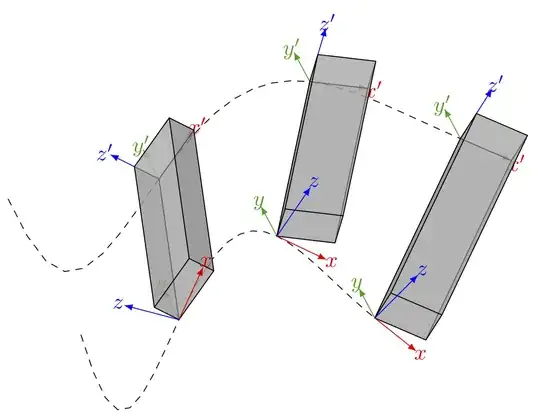
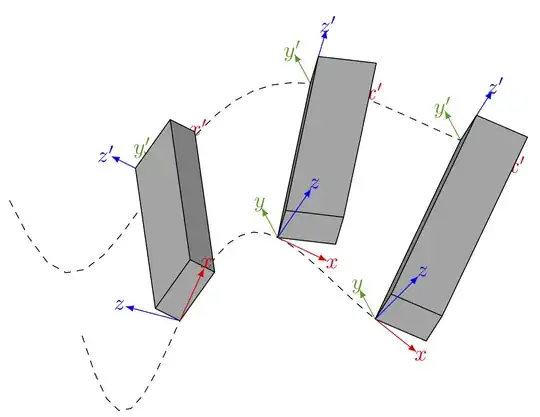
I have the following trajectory, which should depict some path of 2 points on a rigid body. Each point is characterized by a coordinate frame. Now I'd like to use ellipses around the points instead of the cuboids. In a way so that the points appear inside the ellipse/body. This ellipse should only be an indication of the body's position and orientation and should be located in the same plane as the cubes are currently (the lower xy plane).

Currently I am unhappy with the cuboids because for example the top plane of the right most cube is not displayed correctly (same for the middle cube). Also the cuboids are located on top of the frame, whereas I want the frames to be inside.

I think one needs to find a different parameterization for the top trajectory, because this one should be in a fixed distance (something smaller than cube length) to the lower one and it's motion would not be random but given by the distance and angle of the body. Also both points are fixed on the body and experience the same motion, but the top frame should have a fixed relative rotation to their bottom counterpart.

I imagine that ellipses are simpler, but I am happy with any of the two. Thanks!

@Schrödinger's cat: please provide some insight/explaination into how you obtain the rotations and parameterize the points P and Q. Also what is P\Y and Q\Y? Thanks!

\documentclass[border=2mm,tikz]{standalone} 
\usepackage{tikz-3dplot} 
\usetikzlibrary{backgrounds}
\begin{document} 
\tdplotsetmaincoords{60}{-15} 
\begin{tikzpicture}[tdplot_main_coords,scale=1.5,line join=round,>=latex, 
line cap=round,declare function={fA(\t)=-sin(\t*144/(1+\t/5));
fAprime(\t)=pow(60/(5+\t),2)*cos(\t*144/(1+\t/5))*pi/180;
fB(\t)=-sin(\t*216/(1+\t*4/15));
fBprime(\t)=6*pow(90/(15+\t*4),2)*cos(\t*216/(1+\t*4/15))*pi/180;},
pics/coordsys/.style = {
    code = {\tikzset{coordsys/.cd,#1}
        \draw [->,pic actions] (0,0,0) -- +(1,0,0)[red] node[pos=1.1]
        {$\pgfkeysvalueof{/tikz/coordsys/x}$};
        \begin{scope}[on background layer]
        \draw [->,pic actions] (0,0,0) -- +(0,1,0)[green!60!black] node[pos=1.1]
        {$\pgfkeysvalueof{/tikz/coordsys/y}$};
        \end{scope}
        \draw [->,pic actions] (0,0,0) -- +(0,0,1)[blue] node[pos=1.1]
        {$\pgfkeysvalueof{/tikz/coordsys/z}$};
    }
},coordsys/.cd,x/.initial=x,y/.initial=y,z/.initial=z] 
 \draw[dashed] plot[variable=\t,domain=0:5] ({\t},3,{fA(\t)});
 \draw[dashed] plot[variable=\t,domain=0:3.25] ({\t},0,{fB(\t)});
 \foreach \X [count=\Y] in {1,...,3}
 {\draw ({\X*5/3},3,{fA(\X*5/3)}) coordinate (P\Y)
  -- ({\X*3.25/3},0,{fB(\X*3.25/3)}) coordinate (Q\Y);
 \tdplotsetrotatedcoords{0}{atan2(fBprime(\X*3.25/3),1)}{0} 
 \begin{scope}[tdplot_rotated_coords]
 \path (Q\Y) pic{coordsys};
 \pgfmathsetmacro{\myang}{atan2(fBprime(\X*3.25/3),1))}
 \pgfmathtruncatemacro{\itest}{sign(\myang)}
 \pgfmathsetmacro{\cuboiddimx}{2/3}% 2/3 = 1/scale where scale=1.5
 \pgfmathsetmacro{\cuboiddimz}{1/3}% 2/3 = 1/scale where scale=1.5
 \draw[fill opacity=0.5,fill=gray!70]  ($(Q\Y)+(0,0,0)$) 
  --  ($(Q\Y)+(\cuboiddimx,0,0)$) --  ($(Q\Y)+(\cuboiddimx,0,\cuboiddimz)$) 
  -- ($(Q\Y)+(0,0,\cuboiddimz)$) -- cycle;
 \ifnum\itest=-1
 \draw[fill opacity=0.5,fill=gray]  ($(Q\Y)+(\cuboiddimx,0,0)$) 
  --  ($(Q\Y)+(\cuboiddimx,0,\cuboiddimz)$) --  ($(P\Y)+(\cuboiddimx,0,\cuboiddimz)$) 
  -- ($(P\Y)+(\cuboiddimx,0,0)$) -- cycle;
 \else
 \draw[fill opacity=0.5,fill=gray]  ($(Q\Y)+(0,0,0)$) 
  --  ($(Q\Y)+(0,0,\cuboiddimz)$) --  ($(P\Y)+(0,0,\cuboiddimz)$) 
  -- ($(P\Y)+(0,0,0)$) -- cycle;
 \fi 
 \draw[fill opacity=0.5,fill=gray!70]  ($(Q\Y)+(0,0,\cuboiddimz)$) 
  --  ($(Q\Y)+(\cuboiddimx,0,\cuboiddimz)$) --  ($(P\Y)+(\cuboiddimx,0,\cuboiddimz)$) 
  -- ($(P\Y)+(0,0,\cuboiddimz)$) -- cycle;
 \draw[fill opacity=0.5,fill=gray!50]  ($(P\Y)+(0,0,0)$) 
  --  ($(P\Y)+(\cuboiddimx,0,0)$) --  ($(P\Y)+(\cuboiddimx,0,\cuboiddimz)$) 
  -- ($(P\Y)+(0,0,\cuboiddimz)$) -- cycle;

 \end{scope}
 \tdplotsetrotatedcoords{0}{atan2(fAprime(\X*1.25),1)}{0} 
 \begin{scope}[tdplot_rotated_coords]
 \path (P\Y) pic{coordsys={x=x',y=y',z=z'}};
 \end{scope}
 } 
\end{tikzpicture} 
\end{document}

score 2 · Answer 1 · 2019-09-16T21:20:00.430

The problem is that TikZ does not have a 3D engine, so you need to do the 3D ordering yourself. What is 3D ordering? If you have two elements A and B, and if you draw A after B, A will appear to be in front of B. That is, you need to draw closer objects later. What is closer will in general depend on the view angles, which you can set with \tdplotsetmaincoords{60}{-15}, say. If I am not mistaken, you have exchanged the roles of P and Q in your code compared to the original one. However, you did not change the order in which you draw things, and thus it looks wrong. In particular, the xz planes got drawn in the incorrect order. I adjusted the drawing order accordingly and also added a few more planes in the back. I also adjusted the drawing order of coordinate systems.

\documentclass[border=2mm,tikz]{standalone} 
\usepackage{tikz-3dplot} 
\usetikzlibrary{backgrounds}
\begin{document} 
\tdplotsetmaincoords{60}{-15} 
\begin{tikzpicture}[tdplot_main_coords,scale=1.5,line join=round,>=latex, 
line cap=round,declare function={fA(\t)=-sin(\t*144/(1+\t/5));
fAprime(\t)=pow(60/(5+\t),2)*cos(\t*144/(1+\t/5))*pi/180;
fB(\t)=-sin(\t*216/(1+\t*4/15));
fBprime(\t)=6*pow(90/(15+\t*4),2)*cos(\t*216/(1+\t*4/15))*pi/180;},
pics/coordsys/.style = {
    code = {\tikzset{coordsys/.cd,#1}
        \draw [->,pic actions] (0,0,0) -- +(1,0,0)[red] node[pos=1.1]
        {$\pgfkeysvalueof{/tikz/coordsys/x}$};
        \begin{scope}[on background layer]
        \draw [->,pic actions] (0,0,0) -- +(0,1,0)[green!60!black] node[pos=1.1]
        {$\pgfkeysvalueof{/tikz/coordsys/y}$};
        \end{scope}
        \draw [->,pic actions] (0,0,0) -- +(0,0,1)[blue] node[pos=1.1]
        {$\pgfkeysvalueof{/tikz/coordsys/z}$};
    }
},coordsys/.cd,x/.initial=x,y/.initial=y,z/.initial=z] 
 \draw[dashed] plot[variable=\t,domain=0:5] ({\t},3,{fA(\t)});
 \draw[dashed] plot[variable=\t,domain=0:3.25] ({\t},0,{fB(\t)});
 \foreach \X [count=\Y] in {1,...,3}
 {\draw ({\X*5/3},3,{fA(\X*5/3)}) coordinate (P\Y)
  -- ({\X*3.25/3},0,{fB(\X*3.25/3)}) coordinate (Q\Y);
 \tdplotsetrotatedcoords{0}{atan2(fAprime(\X*5/3),1)}{0} 
 \begin{scope}[tdplot_rotated_coords]
 \path (P\Y) pic{coordsys={x=x',y=y',z=z'}};
 \pgfmathsetmacro{\cuboiddimx}{2/3}% 2/3 = 1/scale where scale=1.5
 \pgfmathsetmacro{\cuboiddimz}{1/3}% 2/3 = 1/scale where scale=1.5
 \pgfmathsetmacro{\myopa}{0.6}
 % xz face at y=3 (back of the cuboid)
 \draw[fill opacity=\myopa,fill=gray!50]  ($(P\Y)+(0,0,0)$) 
  --  ($(P\Y)+(\cuboiddimx,0,0)$) --  ($(P\Y)+(\cuboiddimx,0,\cuboiddimz)$) 
  -- ($(P\Y)+(0,0,\cuboiddimz)$) -- cycle;
 % xy face at bottom
 \draw[fill opacity=\myopa,fill=gray!70]  ($(Q\Y)+(0,0,0)$) 
  --  ($(Q\Y)+(\cuboiddimx,0,0)$) --  ($(P\Y)+(\cuboiddimx,0,0)$) 
  -- ($(P\Y)+(0,0,0)$) -- cycle;
 % in order to find out which yz face is to be drawn first,
 % we need to look at an appropriate rotation angle
 \pgfmathsetmacro{\myang}{atan2(fBprime(\X*3.25/3),1))}
 % the sign of the angle determines the ordering
 \pgfmathtruncatemacro{\itest}{sign(\myang)}
 \ifnum\itest=-1
 % the "left" yz face is "hidden"
 \draw[fill opacity=\myopa,fill=gray]  ($(Q\Y)+(0,0,0)$) 
  --  ($(Q\Y)+(0,0,\cuboiddimz)$) --  ($(P\Y)+(0,0,\cuboiddimz)$) 
  -- ($(P\Y)+(0,0,0)$) -- cycle;
 % the "right" yz face is "visible"
 \draw[fill opacity=\myopa,fill=gray]  ($(Q\Y)+(\cuboiddimx,0,0)$) 
  --  ($(Q\Y)+(\cuboiddimx,0,\cuboiddimz)$) --  ($(P\Y)+(\cuboiddimx,0,\cuboiddimz)$) 
  -- ($(P\Y)+(\cuboiddimx,0,0)$) -- cycle;
 \else
 % the "right" yz face is "hidden"
 \draw[fill opacity=\myopa,fill=gray]  ($(Q\Y)+(\cuboiddimx,0,0)$) 
  --  ($(Q\Y)+(\cuboiddimx,0,\cuboiddimz)$) --  ($(P\Y)+(\cuboiddimx,0,\cuboiddimz)$) 
  -- ($(P\Y)+(\cuboiddimx,0,0)$) -- cycle;
 % the "left" yz face is "visible"
 \draw[fill opacity=\myopa,fill=gray]  ($(Q\Y)+(0,0,0)$) 
  --  ($(Q\Y)+(0,0,\cuboiddimz)$) --  ($(P\Y)+(0,0,\cuboiddimz)$) 
  -- ($(P\Y)+(0,0,0)$) -- cycle;
 \fi 
 % top xy face
 \draw[fill opacity=\myopa,fill=gray!70]  ($(Q\Y)+(0,0,\cuboiddimz)$) 
  --  ($(Q\Y)+(\cuboiddimx,0,\cuboiddimz)$) --  ($(P\Y)+(\cuboiddimx,0,\cuboiddimz)$) 
  -- ($(P\Y)+(0,0,\cuboiddimz)$) -- cycle;
 % front xz face
 \draw[fill opacity=\myopa,fill=gray!70]  ($(Q\Y)+(0,0,0)$) 
  --  ($(Q\Y)+(\cuboiddimx,0,0)$) --  ($(Q\Y)+(\cuboiddimx,0,\cuboiddimz)$) 
  -- ($(Q\Y)+(0,0,\cuboiddimz)$) -- cycle;
 \end{scope}
 \tdplotsetrotatedcoords{0}{atan2(fBprime(\X*3.25/3),1)}{0} 
 \begin{scope}[tdplot_rotated_coords]
 \path (Q\Y) pic{coordsys};
 \end{scope}
 } 
\end{tikzpicture} 
\end{document}

As a crosscheck, let's set \pgfmathsetmacro{\myopa}{1}.

If you do not want to do the 3D ordering yourself, you may either look at semi-automatic solutions like this one, or entirely switch to asymptote.

Yes I changed P and Q because I want the cuboids aligned to the lower frames. Can you show me a solution with just a 2d ellipse in the same plane (frame origin to frame origin)? And please comment the code a bit, otherwise its very difficult to figure out. — avermaet, Sep 16 '19 at 17:40
@avermaet I added some explanations. As for the ellipses, one needs to specify a plane they should be in. — , Sep 16 '19 at 21:20
It's ok, I already figured the ellipses out. But maybe you have an idea for this: https://tex.stackexchange.com/questions/508565/tikz-reuse-parts-of-a-plot-and-use-parameters — avermaet, Sep 16 '19 at 21:22

Ellipse in perspective plane around 2 points in 3d space

1 Answers1

Linked